Гетерозиготность природных популяций
Изучение генетической изменчивости.Долгое время проблема регистрации наследственной изменчивости в природных популяциях оставалась открытой. В 20-х годах XX века крупный вклад в ее решение внес выдающийся советский генетик С. С. Четвериков. Вместе со своими учениками Б. Л. Астауровым, Н. К. Беляевым, С. М. Гершензоном, Д. Д. Ромашовым он систематически изучал генетическую изменчивость в природных популяциях дрозофил.Выловленные в природных условиях на Северном Кавказе особи подвергались индивидуальному генетическому анализу, проводились также близкородственные скрещивания. Были определены частоты доминантных и рецессивных мутаций по морфологическим признакам.
Таблица 1 – Частоты генотипов и генов в популяции (N = 100)
| Генотип | Количество индивидов (частота генотипа) | Количество аллелей каждого вида в генотипе | Общее число генов и их процент | Частота гена |
| АА Аа аа |
  20 20
|   120А
20А 120А
20А
  20а
40а 20а
40а
| 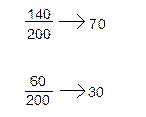
|  А р=0,7 А р=0,7
 а q=0,3 а q=0,3
|
| Всего: | 1,0 |
В 1926 г. С. С. Четвериков опубликовал знаменитую работу «О некоторых моментах эволюционного процесса с точки зрения современной генетики», с которой началась новая теория эволюции – синтетическая. В этой статье он писал что «… популяция, подобно губке, впитывает рецессивные мутации, оставаясь при этом фенотипически однородной». Это скрытый резерв наследственной изменчивости, который создает возможность для эволюции популяций под воздействием естественного отбора.
В 1928 – 1929 гг. американский генетик Г. Меллер разработал точные методы учета летальных мутаций и, таким образом, сделал доступным для исследования еще один класс мутаций. Выяснилось, что природные популяции дрозофил также насыщены рецессивными летальными мутациями.
В начале 60-х гг. появился новый мощный способ изучения изменчивости популяций – гель-электрофорез.
Мерой генетической изменчивости может служить гетерозиготность(H) популяции(или вида), равная средней частоте особей, гетерозиготных по различным локусам. Для ее установления сначала определяют частоты особей, гетерозиготных по каждому изученному локусу. После этого полученные значения усредняют по всем локусам:

где k1…n– частота особей, гетерозиготныхпо первому, второму … n-ному локусам. Естественно, оценка гетерозиготности тем точнее, чем большее количество генов изучено.
Известно, например, что средняя степень гетерозиготности в популяциях растений составляет 17 %, у беспозвоночных – 13,4 %, у позвоночных – 6,6 %, у человека – около 6,7 %.
Понятно, что чем выше уровень гетерозиготности в свободно скрещивающейся популяции, тем больше количество различных сочетаний аллелей у потомков. У человека средняя гетерозиготность составляет 6,7 %. Признав справедливой оценку, что у человека имеется около 30 тыс. локусов, мы придем к выводу, что каждый индивидуум будет гетерозиготен примерно по 2000 локусам.
4. Закон Харди – Вайнберга. Закон Пирсона.
В 1908 г. английский математик Харди и немецкий врач Вайнбергсформулировали независимо друг от другазакон популяционного равновесия:
«… в идеальнойпопуляции частоты генов и генотипов находятся в равновесии и не изменяются в ряду поколений».
Идеальной (или менделеевской)популяцией считается та, для которой соблюдаются следующие 6 условий:
1) новые мутации в данной популяции не появляются;
2) популяция полностью изолирована, т. е. нет миграции особей - носителей генов в популяцию (иммиграции) и из популяции (эмиграции);
3) популяция бесконечно велика, к ней можно применять законы вероятности, т. е. когда крайне маловероятно, что одно случайное событие может изменить частоты аллелей;
4) скрещивания случайны, т. е. происходит чисто случайное образование родительских пар – панмиксия;
5) все аллели равно влияют на жизнеспособность гамет, и потомки от всех возможных скрещиваний имеют равновероятную выживаемость;
6) исходные частоты аллелей одинаковы у обоих полов.
Свой закон Харди и Вайнберг доказали математическим методом, на основании законов Менделя. Какова была логика этих доказательств?
Рассмотрим простейшую ситуацию: в популяции имеется один аутосомный локус, у него два аллеля А и а, их частоты p и q, сумма частот
p + q = 1.В популяции встречаются три генотипа: АА, Аа и аа.

 Возьмем 2 гетерозиготных организма из этой популяции и осуществим их скрещивание:
Возьмем 2 гетерозиготных организма из этой популяции и осуществим их скрещивание:
P: Aа × Аa
 |  |



 G: А а А а
G: А а А а
F1: АА : 2Аа : аа
Напишем решетку Пэннета (для случая, когда р = 0,7; q = 0,3):

Рисунок 2 – Геометрическое представление взаимосвязи между частотами аллелей и частотами генотипов в соответствии с законом Харди - Вайнберга
Из рисунка 2 следует, что частота гомозигот АА равна р2,гомозигот
аа → q2, а гетерозигот Аа → 2pq.
Сумма частот гомо– и гетерозигот должна быть равна 1, т. е.
p2+2pq+q2=(p + q)2=1, что соответствует формуле бинома Ньютона.
Всего возможно 9 вариантов скрещиваний (они представлены в таблице 2).
Таблица 2 – Типы скрещивания и потомки в свободно скрещивающейся популяции
| Тип скрещивания | Возможные генотипы потомков и их частоты | |||
| ♀ | ♂ | АА | Аа | аа |
| АА × АА | p2 | |||
| АА ×Аа | p2 | pq | ||
| АА × аа | pq | |||
 Аа × АА Аа × АА
| p2 | pq | ||
| Аа × Аа | p2 | 2pq | q2 | |
| Аа × аа | pq | q2 | ||
 аа × АА аа × АА
| pq | |||
| аа × Аа | pq | q2 | ||
| аа × аа | q2 | |||
 Итого: Итого:
| 4 p2 | 8 pq | 4 q2 | |
| Соотношение частот генотипов | p2 | 2 pq | q2 | |
Таким образом, соотношение гомо- и гетерозигот в популяции в целом не изменилось по сравнению с потомством одной пары и осталось равным 1 : 2 : 1. Это соотношение не изменится и в следующих поколениях, так как исходные данные одинаковы.
Такая популяция называется равновесной, т. к. частоты генов и генотипов остаются неизменными во всех последующих поколениях.
Популяции, имеющие одинаковые частоты генов, вовсе не обязательно идентичны по частотам генотипов. Например, при частотах генов А0,6и а 0,4 возможны следующие четыре популяции (табл. 3)
Таблица 3 – Частоты генотипов в 4-х возможных популяциях
| Популяция | АА | Аа | аа | р | q |
| I II III IV | 0,20 0,36 0,50 0,60 | 0,80 0,48 0,20 | 0,16 0,30 0,40 | 0,6 0,6 0,6 0,6 | 0,4 0,4 0,4 0,4 |
Хотя они отличаются по частотам генотипов, равновесное состояние всех популяций при изложенных выше условиях, наступающее в первом поколении после случайного скрещивания (а популяция II уже находится в этом состоянии), совершенно одинаково – 0,36АА : 0,48Аа : 0,16аа (рис. 3).

Рис. 3 – Частоты генотипов, представленные одной точкой в равностороннем треугольнике. А. Высота треугольника принята за единицу, а перпендикуляры, опущенные из точки Р (называемой популяционной точкой) на все три стороны треугольника, соответствуют соотношению x, y, и z (или p2, 2pq, q2). Проекция точки Рделит основание треугольника на отрезки XY и YZ, пропорциональные генным частотам p и q соответственно. Б. Четыре популяции (I, II, III и IV) имеют одну и ту же частоту генов (q = 0,4), однако только популяция II находится в состоянии равновесия Харди – Вайнберга. Ее популяционная точка лежит на параболе,представляющей собой локус всех равновесных популяций. Обратите внимание, что вершина параболы (обозначена светлым кружком) соответствует той равновесной популяции, в которой p = q = 0,5 и в которой частота гетерозигот максимальна (2pq = 0,5).
Уравнение позволяет количественно оценивать изменения, происходящие в популяциях, и определять их направление. Если удастся найти в популяции гомозиготных особей, можно подсчитать частоту этого аллеля, а затем и частоты остальных генотипов. Если провести эту работу в нескольких поколениях, можно увидеть, какие процессы идут в генофондах популяций, а затем искать причину.
Как уже указывалось, правило Харди – Вайнберга применимо только в том случае, если выполняются все 6 условий, характеризующих идеальную популяцию. Если нарушается хотя бы одно из них, частоты аллелей начнут изменяться.
Для локуса, имеющего более 2-х аллелей, закон Харди – Вайнберга также выполняется, а формула имеет вид:
(p + q +r)2 =p2 + q2 +r2 + 2pq + 2pr + 2qr = 1,где r– частота третьего аллеля.
Еще раньше, до Харди и Вайнберга, в 1904 г. английский математик К. Пирсон сформулировал закон стабилизирующего скрещивания:
В условиях свободного скрещивания при любом исходном соотношении численности гомозиготных и гетерозиготных родительских форм уже после первого скрещивания внутри популяции устанавливается состояние равновесия.
Как мы видим, закон Пирсона – это частный случай закона Харди – Вайнберга.
Дата добавления: 2017-09-19; просмотров: 403;
