Обоснование и расчет выборочной совокупности

Выборочный метод позволяет делать заключение о характере распределения изучаемых признаков генеральной совокупности на основании рассмотрения некоторой ее части – выборочной совокупности, предполагает различные способы ее формирования, обеспечивающие возможность распространения выводов, полученных при ее рассмотрении, на изучаемую генеральную совокупность.

Основное назначение: применяется для того, чтобы, изучив характеристики минимума объектов, произвести по ним оценку параметров генеральной совокупности. Он значительно сокращает затраты труда, времени, средств на решение той или иной проблемы, повышает качество и надежность процедуры сбора и обработки данных, позволяет изучать объекты, сплошное исследование которых невозможно из-за большого объема затрат.

Область применения: неприменим для изучения объектов, элементы которых не обладают качественной однородностью признаков, значимых с точки зрения целей исследования.

Основные нормативные требования: каждый элемент генеральной совокупности должен иметь определенную, принципиально задаваемую вероятность попасть в выборку. Предполагает наличие необходимой системы показателей генеральной совокупности, отражающих ее качественные и количественные характеристики.

Задачи: предварительный сбор информации об исследуемой совокупности с целью составления основы выборки, введения единиц отбора и анализа; выбор и обоснование схем выборки, организация извлечения единиц отбора из генеральной совокупности по выбранной схеме отбора; расчет характеристик выборочной совокупности; оценка параметров генеральной совокупности по результатам измерения признаков выборочной совокупности.

Генеральная совокупность – множество объектов, являющихся предметом изучения в пределах, очерченных программой социологического исследования и территориально-временными границами.

Выборочная совокупность представляет собой модель генеральной совокупности, результат определенным образом построенного извлечения части элементов генеральной совокупности, выступающих в качестве объектов наблюдения.

Дисперсия – разброс (отклонения) отдельных значений признаков элементов генеральной или выборочной совокупности от средней величины признака. При нулевой дисперсии все единицы отбора имели бы одинаковое, равное среднему значению распределение признаков и для выборки достаточно было бы одной единицы, чтобы обеспечить репрезентативность данных. Чем больше дисперсия, тем больший объем выборочной совокупности потребуется для дальнейшего исследования.

Репрезентативность (от французского слова Representatif – показательный) – свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования. Она означает, что с некоторой заданной наперед или вычисленной погрешностью можно отождествлять установленное на выборочной совокупности распределение изучаемых признаков с их действительным распределением в генеральной совокупности. Оценка репрезентативности выводится на основе анализа и расчета ошибок: процедурных (допущенных при регистрации признаков) и случайных (зависящих от степени изменчивости изучаемого признака).

Ошибка выборки – мера подобия выборочной совокупности генеральной. Типы ошибок: случайные, систематические, ошибки смещения.

Ошибки репрезентативности – мера отклонения статистической структуры выборки от структуры соответствующей ей генеральной совокупности. В практических исследованиях отождествляют дисперсию генеральной совокупности с дисперсией выборочной совокупности. Из математической статистики известно, что с определенной вероятностью можно утверждать, что отклонения выборочной средней от генеральной не превышает некоторой величины, которая называется предельной ошибкой репрезентативности.

Для определения объема выборки в условиях случайного бесповторного отбора используется следующая формула:

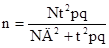, где

где Д – предельная ошибка репрезентативности (в задачах социологического класса Д = 5%); t – коэффициент доверия (в задачах социологического класса равен 2); N – объем генеральной совокупности; р - доля объектов, обладающих данным признаком; q – 1-р – доля объектов, не обладающих данным признаком.

Основа выборки – перечень элементов генеральной совокупности, если он удовлетворяет требованиям полноты, точности, адекватности, удобства работы с ним, отсутствия дублирования единиц анализа. В качестве основы могут служить алфавитные списки сотрудников учреждения, домовые книги, картотеки отделов кадров. Наиболее полно удовлетворяет требованиям выборки социальные карты организаций, регионов, представляющие собой пространственные распределения показателей для определенных организаций или регионов и включающие демографические, экономические, политические и другие социальные показатели.

Виды выборок: случайная (вероятностная), неслучайная, квотная, целенаправленная, одноступенчатая, многоступенчатая.

Единицы отбора – элементы генеральной совокупности, отбираемые на каждом этапе выборки.

Закон больших чисел – статистический закон, выражающий связь статистических показателей выборочной и генеральной совокупности. Фактические значения статистических показателей, полученные по некоторой выборке, всегда отличаются от теоретических значений, свойственных генеральной совокупности. Закон больших чисел состоит в том, что фактические данные все больше приближаются к теоретически ожидаемым значениям по мере возрастания числа наблюдений. Из закона больших чисел следует, что для каждого параметра генеральной совокупности может быть рассчитан минимальный объем выборочной совокупности, при котором (при условии обеспечения репрезентативности выборки) разница между теоретическими и фактическими значениями параметров не превышают заданной величины.