Момент инерции диска (цилиндра) относительно оси симметрии z (проходящей через точку 0 перпендикулярно плоскости рисунка).

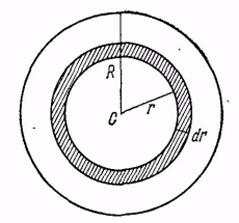
	Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r наружным радиусом r + dr. Площадь такого кольца 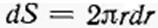.   Его момент инерции равен
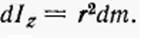
Рис. 7.3. Момент инерции однородного диска. Разбиение на кольца

По определению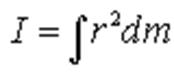

Элемент массы представим в виде

,

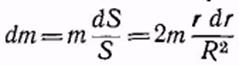тогда

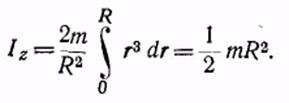
Момент инерции однородного шара массы т и радиуса R относительно оси проходящей через центр.

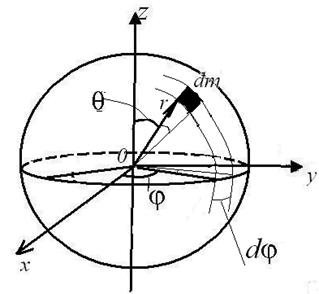
Рассмотрим элемент объема шара в сферической системе координат

http://akak-ich.ru/phyz-mech_1.php необработанный источник.

Рис. 7.4 Момент инерции однородного шара относительно оси, проходящей через его центр

Удобнее рассматривать в сферической системе координат, тогда момент инерции элемента dm равен:

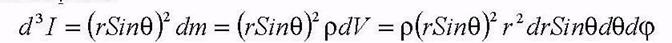
где 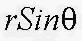расстояние кусочка массы dm до оси вращения,

r - плотность шара. Интегрируя по всем переменным:

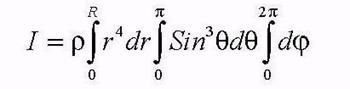
и учитывая, что масса шара равна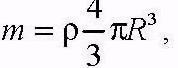

получаем момент инерции шара относительно оси симметрии:

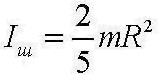
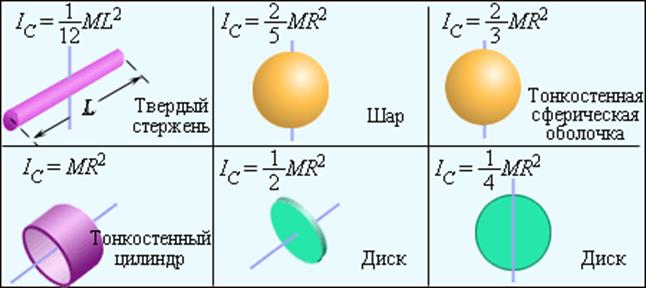
Момент инерции тонкостенного кругового цилиндра, сплошного цилиндра, стержня – самостоятельно. (источник – Детлаф, Яворский 2002 г. Глава 6. С. 55 – 56 )