Момент импульса частицы.
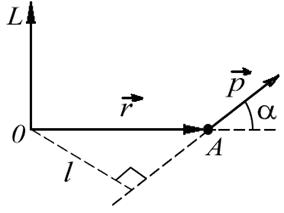
Моментом импульса частицы А относительно точки O (рис. 5.1) называют вектор 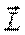 , равный векторному произведению векторов
, равный векторному произведению векторов 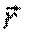 и
и 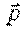 :
:
| 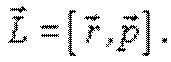 (5.2)
модуль вектора (5.2)
модуль вектора
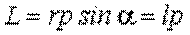 (5.3) (5.3)
|
| Рис. 5.1. Определение вектора момента импульса |
2. Уравнение моментов. Моментсилы
Продифференцируем уравнение (5.2) по времени:
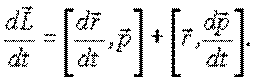
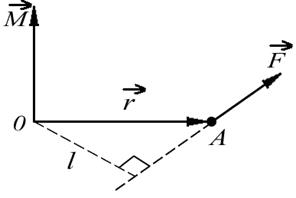
Моментом силы F относительно точки O (рис. 5.2) называют вектор 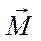 , равный векторному произведению векторов
, равный векторному произведению векторов 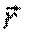 и
и 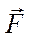 :
:
| Для неподвижной т. О:
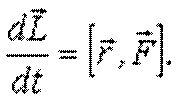
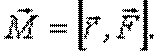
|
| Рис. 5.2 Определение вектора момента cилы |
Модуль вектора М равен
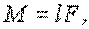
| (5.5) |
где 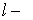 плечо вектора
плечо вектора 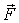 относительно точки O (рис. 5.2).
относительно точки O (рис. 5.2).
Итак:
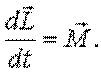 или или 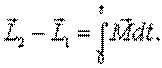
| (5.5) |
Величина в правой части – импульс момента силы. В итоге получено следующее утверждение: приращение момента импульса частицы (твердого тела) за любой промежуток времени равно импульсу момента силы за это же время.
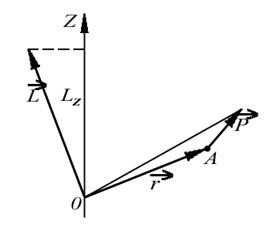
Моментом импульса относительно оси z называют проекцию на эту ось вектора 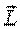 , определенного относительно произвольной точки О данной оси (рис. 5.3). Аналогично вводят и понятие момента силы относительно оси. Их обозначают соответственно
, определенного относительно произвольной точки О данной оси (рис. 5.3). Аналогично вводят и понятие момента силы относительно оси. Их обозначают соответственно 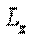 и
и 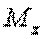 .
.
| Значения проекций 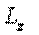 и и 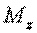 не зависят от выбора точки О на оси z. не зависят от выбора точки О на оси z.
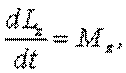 (5.6)
Если (5.6)
Если 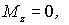 то то 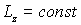 . . 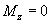 . .
|
| Рис. 5.3. Определение момента импульса и момента силы относительно оси |
Дата добавления: 2017-06-02; просмотров: 1070;
