Если . то – полный импульс замкнутой системы остается неизменным при любых движениям системы и взаимодействиях внутри нее.
Импульс силы:
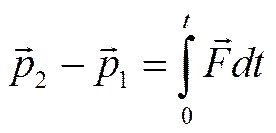
| (4.17) |
Порядок решения задачи динамики:
1. Понять предложенную задачу (увидеть физическую модель).
2. Провести анализ физической модели (построить математическую модель явления):
1) выбрать систему отсчета;
2) найти все силы, действующие на тело, и изобразить их на чертеже. Определить (или предположить) направление ускорения и изобразить его на чертеже;
3) записать уравнение второго закона Ньютона в векторной форме и перейти к скалярной записи, заменив все векторы их проекциями на оси координат;
4) исходя из физической природы сил, дополнительно выразить силы через величины, от которых они зависят;
5) если в задаче требуется определить положение или скорость точки, то к полученным уравнениям динамики добавить кинематические уравнения.
3. Полученную систему уравнений решить относительно искомой величины.
4. Проверить решение и критически оценить с точки зрения физического смысла.
Пример 1:
4.1. Движение точки массой m = 1 кг задано уравнениями:
х = 6t3 – t2 + 5 (м), у = 4t2 + t – 7 (м).
Определить силу, действующую на точку и модуль скорости точки в момент t = 1 с.
Решение. Для составления уравнений движения точки в проекциях на оси координат нужно продифференцировать два раза исходные уравнения:
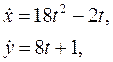
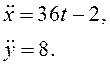
Уравнения движения тела в проекциях на оси координат:
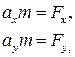
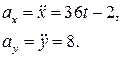
В момент времени t = 1 с:
ах = 36 – 2 = 34, ау =8.
Тогда, при m = 1 кг:
Fx = 34 H, Fу = 8 H.
Модуль силы, действующий на точку в момент t = 1 с, равен:
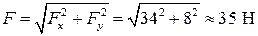 , F = 35 H.
, F = 35 H.
Направляющие косинусы силы:
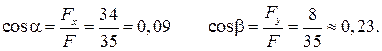
При t = 1 с проекции скорости на оси равны:
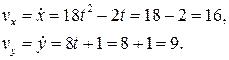
Модуль скорости равен:
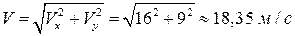 .
.
Ответ. V = 18,35 м/с.
ПРИМЕР 2.
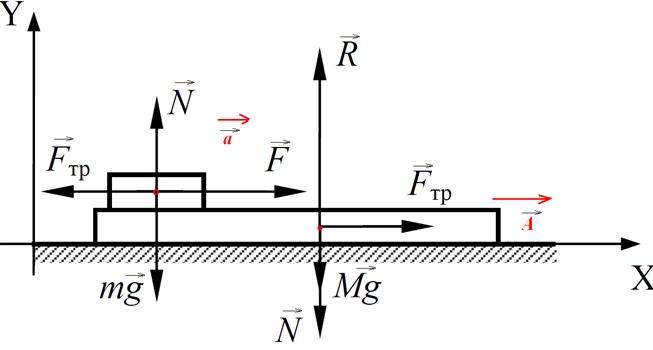
На доске массой М лежит брусок массой m. Коэффициент трения между доской и бруском равен μ. Доска может двигаться по гладкой горизонтальной поверхности. К бруску прикладывается горизонтальная сила 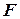 , модуль которой зависит от времени по закону
, модуль которой зависит от времени по закону 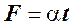 , где α=const. Определить скорости бруска
, где α=const. Определить скорости бруска 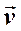 и доски
и доски 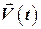 спустя время t после начала действия силы.
спустя время t после начала действия силы.
t0
Решение разбивается на два этапа. 0 ≤ t ≤ t0 t > t0
Выберем систему координат так, как показано на рис., и изобразим силы, действующие на тела системы.
Уравнения движения бруска и доски в проекциях на оси системы координат, одинаковые на первом и втором этапах движения, уравнение кинематической связи (при t ≤ t0) и закон Амонтона – Кулона (при t > t0). Введем обозначения: a и A – проекции ускорений бруска и доски на ось X.
Общую систему уравнений представим в виде:
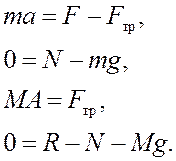 (1)
(1)
Используем также заданный в условии задачи закон изменения модуля силы F со временем: 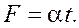
При 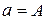 :
:
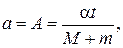
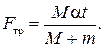 (2)
(2)
Для силы трения скольжения можно записать: 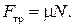 Тогда
Тогда
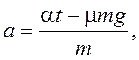
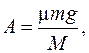
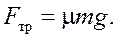 (3)
(3)
В соответствии с законом Амонтона – Кулона максимальное значение силы трения покоя равно силе трения скольжения , значит, из (2) и (3) получим:
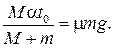 (4)
(4)
Выражение (4) позволяет найти момент времени t0, в который брусок начинает скользить по доске:
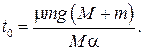 (5)
(5)
Таким образом:
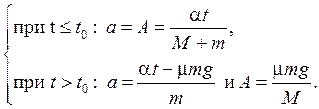 (6)
(6)
Используя полученные выражения для ускорений тел системы (6), можно теперь определить и законы изменения скоростей этих тел.
При t ≤ t0 доска и брусок движутся как одно тело, значит, их скорости меняются одинаковым образом и к моменту времени t окажутся равными:
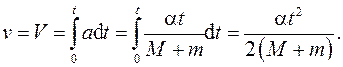 (7)
(7)
Тогда при t >t0 скорость бруска можно определить как сумму (7) и интеграла от второго уравнения (6) для a:
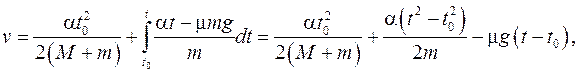 (8)
(8)
а скорость доски как сумму (7) и интеграла от второго уравнения (6) для А:
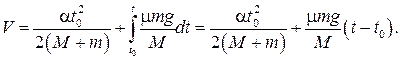 (2.59)
(2.59)
ПРИМЕР 2
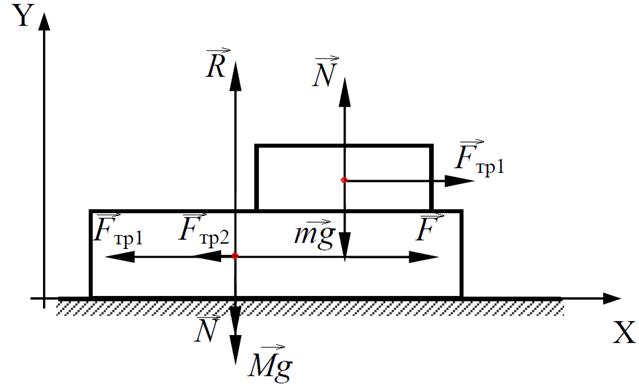
На столе лежит доска массой М=1 кг, а на доске – груз массой m=2 кг. Какую силу F нужно приложить к доске, чтобы она выскользнула из-под груза? Коэффициент трения между грузом и доской равен μ1=0,25, а между доской и столом – μ2=0,5.
Решение.
Запишем уравнения движения груза и доски в проекциях на оси выбранной системы координат:
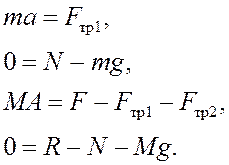 (1)
(1)
Здесь a и A – проекции ускорений груза и доски на ось ОX.
Используем закон Амонтона – Кулона, описывающий свойство силы трения скольжения:
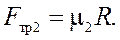 (2)
(2)
Значение силы F0, действующей на груз, при котором начнется его скольжение по доске, можно определить из условий:
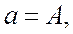 (3)
(3)
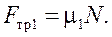 (4)
(4)
Решая полученную систему уравнений (2)–(4) относительно F0, получим:
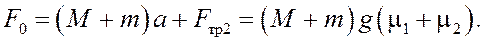 (5)
(5)
Или:
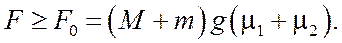 (6)
(6)
Или:
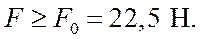 (7)
(7)
Ответ. 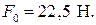
Дата добавления: 2017-06-02; просмотров: 1563;
