Вращательное движение твердого тела
Степени свободы
Можно выделить пять видов движения твердого тела:
1)поступательное,
2) вращательное,
3) плоское,
4)сферическое,
5)свободное.
Первые два движения являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупности (это будет показано на примере плоского движения).
1. Поступательное движение твердого теламожет быть полностью описано, если известны зависимость от времени радиус-вектора 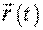 любой точки этого тела и его положение в начальный момент, (см. предыдущий раздел).
любой точки этого тела и его положение в начальный момент, (см. предыдущий раздел).
Вращательное движение твердого тела
Для описания вращательного движения используются следующие величины:
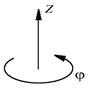
угол поворота как вектор 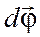 , направление вектора связано с направлением вращения правилом правого винта; ( просто: если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен вектор углового поворота тела).
, направление вектора связано с направлением вращения правилом правого винта; ( просто: если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен вектор углового поворота тела).
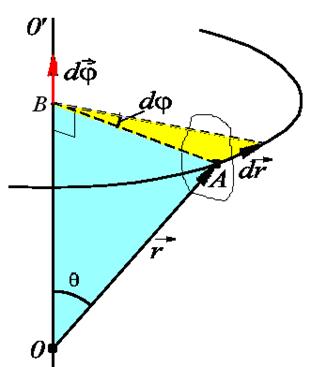
| Рис. 3.6.Вращение твердого тела вокруг неподвижной оси
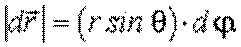
|
или в векторном виде 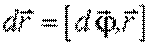
| (3.11) |
Только бесконечно малые повороты можно рассматривать как векторы.
Вектор угловой скорости 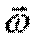 определяют так
определяют так
 , ,
| (3.12) |
где dt - интервал времени, за который тело совершает поворот 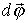 .Направление вектора связано с направлением вращения правилом правого винта; (просто: если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.)
.Направление вектора связано с направлением вращения правилом правого винта; (просто: если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.)
Вектор 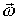 является аксиальнымвектором.
является аксиальнымвектором.
Изменение вектора 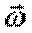 со временем характеризуют вектором углового ускорения
со временем характеризуют вектором углового ускорения 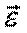 , который определяют соотношением
, который определяют соотношением
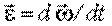 , ,
| (3.13) |
Вектор направлен вдоль линии направления угловой скорости: сонаправлен или противонаправлен с ней.
То есть, направление вектора 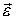 совпадает с направлением
совпадает с направлением 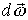 - приращения угловой скорости
- приращения угловой скорости 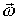 . Вектор
. Вектор 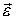 , как и
, как и 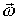 , также аксиальный.
, также аксиальный.
|
| Рис. 3.7.Введение понятия угловых векторов |
Проекции 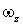 и
и 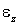 векторов
векторов 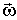 и
и 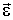 на ось
на ось 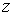 определяются формулами:
определяются формулами:
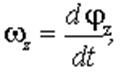
| (3.14) |
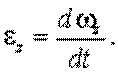
| (3.15) |
В этих формулах 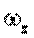 и
и 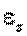 - алгебраические величины.
- алгебраические величины.
По известной зависимости 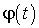 , называющейся законом вращения тела, формулы (3.14) и (3.15) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости
, называющейся законом вращения тела, формулы (3.14) и (3.15) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости 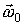 и угла j0 в начальный момент времени, можно найти
и угла j0 в начальный момент времени, можно найти 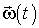 и
и 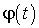 .
.
Дата добавления: 2017-06-02; просмотров: 1279;
