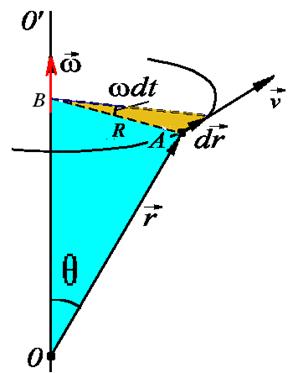
Установим связь между линейными и угловыми величинами.
| 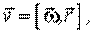 (3.16) (3.16)
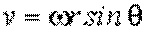 или
или

|
| Рис. 3.8. Связь линейных и угловых величин при вращении |
Продифференцируем (3.16) по времени:
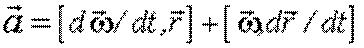 , т.е.
, т.е.
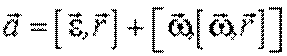 . .
| (3.17) |
Ось вращения неподвижна, 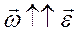 , поэтому первое слагаемое в (3.18) – тангенциальное ускорение
, поэтому первое слагаемое в (3.18) – тангенциальное ускорение 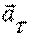 , а второе слагаемое – нормальное (центростремительное ) ускорение
, а второе слагаемое – нормальное (центростремительное ) ускорение 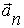 .
.
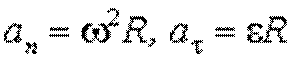 ,
,
Модуль полного ускорения можно найти как
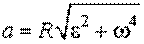 .
.
Сложение угловых скоростей.
Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей ОА и ОВ (рис. 3.12).
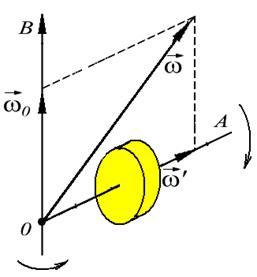
| Рис. 3.13. Сложение угловых скоростей
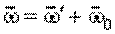 Или
Или 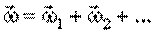 (3.20) (3.20)
|
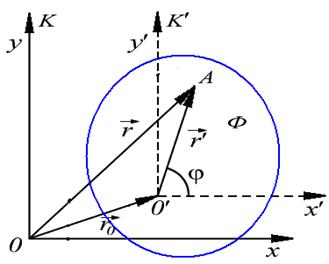
Связь кинематических величин в различных системах отсчета.
Поступательное относительное движение систем. Пусть в К-системе радиус-вектор 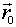 – начало отсчета
– начало отсчета 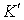 - системы, ее скорость
- системы, ее скорость 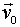 и ускорение
и ускорение 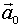 . Ясно, что
. Ясно, что 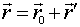 (рис. 3.13).
(рис. 3.13).
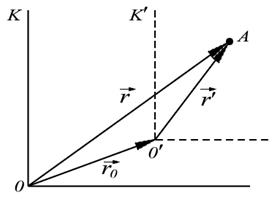
| Рис. 3.13.Поступательное относительное движение
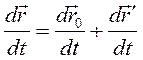
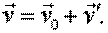 (3.21) (3.21)
|
Дифференцируя (3.21) по времени найдем формулу преобразования ускорения:
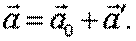
| (3.22) |
ПРИМЕРЫ
ПРИМЕР 1. Колесо вращается вокруг неподвижной оси так, что угол φ его поворота зависит от времени как 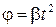 , где β=const. Найти полное ускорение а точки А на ободе колеса в момент времени t, если скорость точки А в этот момент имела значение v.
, где β=const. Найти полное ускорение а точки А на ободе колеса в момент времени t, если скорость точки А в этот момент имела значение v.
Решение. Угловая скорость вращения колеса ω в момент времени t равна:
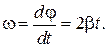
Так как линейная скорость v точки А в этот момент времени связана с угловой скоростью ω соотношением 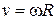 , то радиус колеса R равен:
, то радиус колеса R равен:
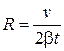 ,
,
а нормальное ускорение этой точки определяется выражением:
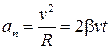 .
.
Тангенциальное ускорение точки А в момент времени t равно:
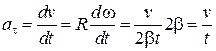
и, следовательно, полное ускорение в этот момент времени записывается в виде:
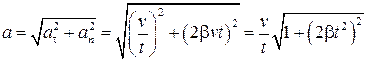 .
.
Ответ. 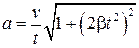 .
.
3. Плоское движение твердого тела.
Плоскопараллельным или плоским называют движение твердого тела, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.
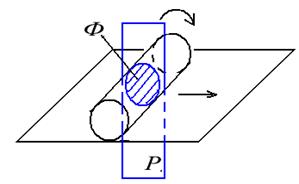
Плоское движение тел является одним из наиболее распространенных в технике. Плоское движение совершают тела качения (колеса, катки, цилиндры ) на прямолинейном участке пути; отдельные детали механизмов, предназначенных для преобразования вращательного движения одного тела в поступательное или колебательное другого; шестерни планетарных передач.
Движение тела может рассматриваться как результат сложения поступательного движения и вращения тела относительно некоторой линии, которая называется мгновенная ось вращения.
|
| Рис. 3.9. Определение плоского движения |
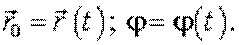 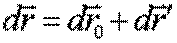 (3.18) (3.18)
|
где 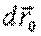 - перемещение точки
- перемещение точки 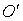 , a
, a 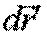 - перемещение точки А относительно системы K'. Перемещение
- перемещение точки А относительно системы K'. Перемещение 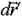 вызвано вращением тела вокруг неподвижной в K-системе оси, проходящей через точку
вызвано вращением тела вокруг неподвижной в K-системе оси, проходящей через точку 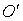
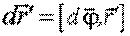 .
.
 , ,
| (3.19) |
Скорость 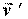 - это скорость частицы А относительно поступательно движущейся системы отсчета, жестко связанной с точкой
- это скорость частицы А относительно поступательно движущейся системы отсчета, жестко связанной с точкой 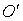 .
.
Дата добавления: 2017-06-02; просмотров: 807;
