Сравнительная оценка проектов с различной
Продолжительностью
На практике часто возникает необходимость оценки и сравнения ИП с различным сроком жизни. Для устранения влияния временного фактора используются следующие методы [8, 67–69, 74, 79, 80]:
1. Метод цепного повтора в рамках общего периода действия рассматриваемых проектов.
Логика расчета:
а) рассматриваются два проекта А и В, сроки действия которых соответственного i и j лет. Определяется наименьшее общее кратное им тот период времени, в течение которого каждый из проектов может быть реализован целое число раз:
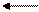 A: i=3 A: i=3
|   12 12
| n=4 |
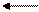 B :j=4 B :j=4
| n=3 |
б) каждый проект рассматривается как повторяющейся в рамках общего периода действия. Рассчитывается NPV каждого проекта при n-м его повторении в рамках общего периода действия:
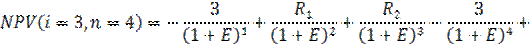
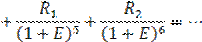
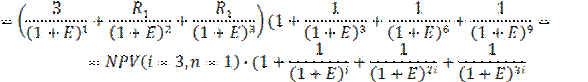
| (11.97) |
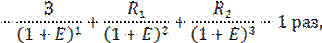
| (11.98) |
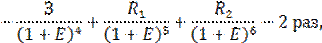
| (11.99) |
соответственно n = 4 – для реализации четыре раза;
в) сравнивается NPV повторяющихся проектов, выбирается тот из них, для которого суммарный NPV повторяющегося потока имеет наибольшее значение.
2. Метод бесконечно цепного повтора сравниваемых проектов.
Если анализируется несколько проектов, существенно различающихся по продолжительности, использование метода цепного повтора в рамках общего периода действия нецелесообразно, так как расчеты будут очень сложными. Их можно сократить, если предположить, что каждый из анализируемых проектов может быть реализован неограниченное число раз.
В этом случае число слагаемых в формуле NPV (I, n) будет стремиться к бесконечности. А NPV (I, ∞) можно найти по формуле бесконечно убывающей геометрической прогрессии, потому что NPV при дисконтировании будет уменьшаться в производстве:
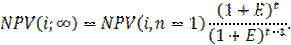
| (11.100) |
Из всех сравниваемых проектов проект, имеющий наибольшее значение NPV(i, ∞), является предпочтительным.
3. Метод эквивалентного аннуитета.
Эквивалентный аннуитет – аннуитет, который имеет ту же продолжительность, что и оцениваемый проект, и ту же величину текущей стоимости, что и NPV данного проекта.
Логика расчета:
а) рассчитывается NPV однократной реализации каждого из сравниваемых проектов;
б) для каждого проекта находится эквивалентный аннуитет, текущая стоимость которого в точности равна NPV проекта, т.е. рассчитывается величина аннуитетного платежа:
· tA=10 NPVA = PAA стремится к ЕАА;
· tВ=14 NPVВ = PAВ стремится к ЕАВ;
· ЕА – R член аннуитета
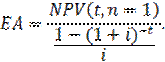
| (11.101) |
Найденный аннуитет может быть заменен бессрочным аналогом с той же самой величиной аннуитетного платежа. Далее рассчитывается текущая стоимость бессрочного аннуитета для каждого проекта, и тот из них, у которого эта величина окажется больше, является более предпочтительным.
Дата добавления: 2017-06-02; просмотров: 564;
