ОСНОВНЫЕ ПОЛОЖЕНИЯ ПРИНЦИПА ЭЛЛИОТТА

1. Все изменения в направлении главного тренда называются волнами импульса.

2. Все волны, направленные против главного тренда, называются волнами коррекции.

3. Каждая волна импульса состоит их пяти волн меньшего размера.

4. Каждая волна коррекции состоит из трех волн меньшего размера.

5. Одна из трех волн импульса является растянутой, т.е. имеет большую по сравнению с другими продолжительность. Такая волна состоит обычно из девяти меньших волн. Обычно растянутой бывает третья волна импульса.

6. Продолжительность растянутой волны импульса составляет, как правило, 1,618 от длительности обычной волны импульса (отношение чисел Фибоначчи).

7. С завершением последней из восьми волн (пяти - роста и трех - снижения) завершается полный цикл. Коррекция обычно выводит цены на уровень 4-й волны.

8. Полный цикл представляет собой две волны большего цикла.

9. Форма, продолжительность и сложность коррекций разнятся. Например, 2-я волна может корректировать цены до уровня 62% от 1-й волны, 4-я волна может произвести откат до уровня 38% от 3-й волны,

10. Если 1-я волна - растянутая волна из пятерки, 4-я волна может опустится до ее уровня, достигнув уровня корректировки 2-й волны, но не дальше.

11. Пятая волна импульса может иногда принимать форму диагонального треугольника. При этом ее 4-я волна опускается ниже пика 1-й волны. После образования треугольника происходит резкая коррекция, сводящая на нет весь подъем от основания треугольника.

Принцип Эллиотта, как уже упоминалось, непосредственно связан с соотношениями чисел Фибоначчи. Высота соседних волн по Эллиотту соотносится в отношениях 1,618 (между волнами импульса); 0,382; 0,5; 0,618 (высота волн коррекции по отношению к предшествующей волне импульса).

ИНДИКАТОРЫ

Индикаторы делятся на три группы: отслеживающие тренды, осцилляторы и характеристические.

Отслеживающие тренды включают: скользящие средние МА (Moving Averages), MACD, MACD-гистограммы, Систему направлений (Directional System), индикатор Равновесного объема (OBV), Аккумуляции/Распыления и др. Они относятся к классу сопровождающих или запаздывающих - их разворот следует за разворотом тренда.

Осцилляторы помогают выявить точки разворота тренда. К ним относятся: Стохастик-индикатор, Показатель скорости изменения, Сглаженный Показатель скорости изменения, Индексы момента (Momentum), RSI, луч Элдера, Индекс Силы, %R Вильямса, Канальный индекс товаров (CCI) и др. Осцилляторы относятся к сопровождающим или опережающим индикаторам, изменения в них часто предшествуют действительным изменениям цен на рынке.

Характеристические индикаторы показывают внутреннее соотношение сил между медведями и быками. Их можно разделить на две группы: макроэкономические и индикаторы настроения рынка. Индикаторы первой группы анализируют общую экономическую ситуацию и изменения "макроэкономической среды" могущие повлиять на рынок. Ко второй группе относятся индикаторы "ширины" рынка (индикаторы фондового рынка) и "психологические" индикаторы. Индикаторы этой группы пытаются определить по определенным внешним признакам направление внутренних, "глубинных" процессов на рынке.

Индикаторы делятся на несколько видов по способу их применения.

1. Трендовые индикаторы
2. Осцилляторы

Трендовые индикаторы – это индикаторы, которые хорошо работают в трендовом участке рынка, и хорошо определяют тренд.

Осцилляторы – это индикаторы, которые всегда пытаются предсказать будущее, но при этом совершают больше ошибок.

СКОЛЬЗЯЩИЕ СРЕДНИЕ

Простые скользящие средняя (Moving Averages- МА) (simple)-вычисляется путем сложения и усреднения набора чисел.

Взвешенные скользящие средние (weighted)- каждой из цен анализируемого промежутка времени придает вес, в соответствии с объемами сделок, совершенными в данный промежуток времени.

Экспоненциальные скользящие средние (exponential)- умножение цены на вес. Но и учитывают весь диапазон цен.

Смещенные скользящие средние DMA- Displased Moving Averages

Скользящие средние нашли широкое применение в эконометрике.

Два самых популярных типа скользящих средних – это Простая Скользящая средняя (SMA), взвешенная (WMA) и Экспоненциальная Скользящая средняя (EMA).

Простая Скользящая средняя (SMA)

Простая Скользящая средняя формируется путем вычисления средней цены рыночного инструмента за указанное число периодов. Хотя возможно формировать Скользящие средние исходя из цены открытия, максимума и минимума, большинство Скользящих средних использует цену закрытия.

Простое скользящее среднее определяется по формуле:

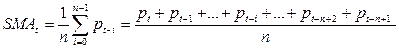, (5)

где SMA_t — значение простого скользящего среднего в точке t; n — количество значений исходной функции для расчёта скользящего среднего; p_t-i — значение исходной функции в точке t-i.

Последующее значение скользящего среднего рассчитывается на основе предыдущего:

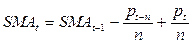(6)

где SMA_t-1 — предыдущее значение простого скользящего среднего, p_t-n — значение исходной функции в точке t=n; p_t — значение исследуемой функции точке t (в случае временного ряда последнее значение).

Например: значение 5-дневной Простой Скользящей средней рассчитано суммированием цен закрытия в течение прошлых 5 дней и делением общей суммы на 5.

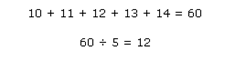
Вычисление повторяется для каждого ценового бара на графике. Затем средние значения соединяются и формируют гладкую изгибающуюся линию - скользящую среднюю линию. Продолжим наш пример: если следующая цена закрытия равна 15, то этот новый период будет добавлен, а самый первый день, для которого значение равно 10, будет исключен. Новое значение 5-дневной Простой Скользящей средней будет рассчитано следующим образом:

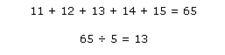
За последние 2 дня, SMA продвинулась от 12 до 13. Поскольку новые дни добавляются, прошлые дни будут выбывать и Скользящая средняя будет продолжать двигаться дальше.

Взвешенное скользящее среднее (WMA).

При построении скользящей средней некоторые значение исходной функции целесообразно сделать более значимым. Например, последние значения цен более актуальные и могут быть весомее предыдущих.

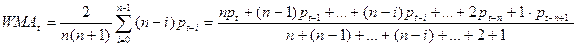(7)

Взвешенное скользящее среднее, как и экспоненциальное, придает более поздним данным больше “веса”, но оно делает это более выражено и проще. При просчете 5-ти дневного взвешенного скользящего среднего, мы придаем текущей цене пятикратный вес, вчерашней — четырехкратный, позавчерашней — трехкратный и т.д., а потом делим сумму всех произведений на сумму добавленного веса. Т.е.

(1·8+2·8+3·9+4·10+5·11)/(1+2+3+4+5) = 146/15 = 9,73.

Какую Скользящую среднюю использовать зависит от вашего стиля торговли и ваших предпочтений. Простая Скользящая средняя очевидно имеет запаздывание, но Экспоненциальная Скользящая средняя может быть склонна к более быстрым прорывам. Некоторые трейдеры предпочитают использовать Экспоненциальные Скользящие средние для более коротких периодов времени для более быстрого отображения изменений. Некоторые инвесторы предпочитают для долгосрочных периодов Простые Скользящие средние, чтобы определять долгосрочные изменения трендов. Кроме того, многое будет зависеть от конкретного рыночного инструмента.

Экспоненциальная Скользящая средняя (EMA)

Чтобы снизить запаздывание в Простых Скользящих средних, трейдеры часто используют Экспоненциальные Скользящие средние (также называемые «Скользящие средние взвешенные по экспоненте»). EMA уменьшает запаздывание, придавая больший вес недавним ценам относительно более ранних цен.

Экспоненциально взвешенное скользящее среднее рассчитывается следующим образом:

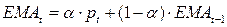(8)

где EMA_t — значение экспоненциального скользящего среднего в точке t (последнее значение, в случае временного ряда), EMA_t-1 — значение экспоненциального скользящего среднего в точке t-1 (предыдущее значение в случае временного ряда), p_t — значение исходной функции в момент времени 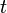(последнее значение в случае временного ряда), α (сглаживающая константа) — коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.

Первое значение экспоненциального скользящего среднего обычно принимается равным первому значению исходной функции:

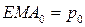(9)

Коэффициент α равен:

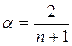(10)

где n - указанное число периодов.

Придаваемый недавним ценам больший вес зависит от периода Скользящей средней. Чем короче период EMA, тем больший вес будет придаваться самой последней цене. Например: 10-периодная Экспоненциальная Скользящая средняя придаст самой последней цене вес 18.18 %, в то время как 20-периодная EMA только 9.52 %.

Вычисление EMA более затруднительно, чем вычисление SMA. Важно запомнить, что Экспоненциальные Скользящие средние придают больше веса последним ценам. Также, они будут реагировать быстрее на недавние изменения цен, чем Простые Скользящие средние. Ниже приведена формула вычисления.