Уравнения движения колеса по недеформируемой поверхности при прямолинейном движении
В зависимости от приложенного к колесу момента различают: колесо ведомое (М=0), ведущее (М=Мк-крутящий момент) и тормозное (М=Мт- тормозной момент).
Рассмотрим уравнения мощностей и сил, приложенных к каждому из этих колес.
Ведомое колесо
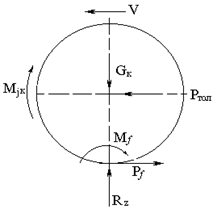 На ведомое колесо действуют нагрузка Gк и толкающая сила Ртол, приложенные в центре колеса. Со стороны опорной поверхности будет действовать нормальная реакция Rz, момент сопротивления качению Мf и сила сопротивления качению Рf , направленная противоположно вектору скорости V.
На ведомое колесо действуют нагрузка Gк и толкающая сила Ртол, приложенные в центре колеса. Со стороны опорной поверхности будет действовать нормальная реакция Rz, момент сопротивления качению Мf и сила сопротивления качению Рf , направленная противоположно вектору скорости V.
Если колесо будет двигаться с ускорением, тогда дополнительно возникнет инерционный момент
Мj к = 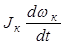 ,
,
где Jк – момент инерции колеса относительно оси вращения;
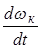 - угловое ускорение колеса.
- угловое ускорение колеса.
Рис 3.3 Ведомое колесо
Составим уравнения мощностей, считая, что подводимая к колесу мощность расходуется на преодоление сопротивления качению и разгон колеса. Тогда
N тол = Nf + Njк, (3.2)
где N тол – мощность, создаваемая толкающей силой Ртол , и равная
N тол = Ртол V;
Nf – мощность сопротивления качению, равная Nf = fGкV = Pf V;
Njк – мощность, вызванная инерционным моментом
Njк = Мjк × wк = Jк 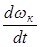 wк;
wк;
где wк – угловая скорость вращения колеса.
Подставив полученные выражения в уравнение (3.2), имеем
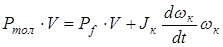 , (3.3)
, (3.3)
Если правую и левую стороны уравнения (3.3) разделить на V, учитывая, что V = wк×rк , тогда получим уравнение сил, действующих на ведомое колесо
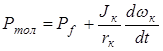 .
.
При равномерном движении колеса это уравнение запишется так
Ртол = Рf .
Ведущее колесо
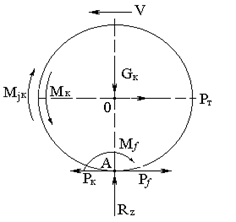 Расчетная схема сил, действующих на ведущее колесо, приведена на рисунке 3.4. На ведущее колесо действуют крутящий момент Мк, который подводится к нему от двигателя через трансмиссию, нагрузка на колесо Gк и тяговая сила Рт, приложенная в центре колеса. Крутящий момент Мк, подведенный к колесу, вызывает тангенциальную реакцию опорной поверхности, направленную по вектору V, которую называют окружной силой Рк, равной Рк =
Расчетная схема сил, действующих на ведущее колесо, приведена на рисунке 3.4. На ведущее колесо действуют крутящий момент Мк, который подводится к нему от двигателя через трансмиссию, нагрузка на колесо Gк и тяговая сила Рт, приложенная в центре колеса. Крутящий момент Мк, подведенный к колесу, вызывает тангенциальную реакцию опорной поверхности, направленную по вектору V, которую называют окружной силой Рк, равной Рк = 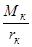 ,. где rк – радиус колеса.
,. где rк – радиус колеса.
Рис.3.4 Ведущее колесо
Со стороны опорной поверхности действуют равнодействующая нормальных реакций Rz , сила сопротивления качению Рf и момент сопротивления качению Мf. При ускоренном движении возникает дополнительно инерционный момент Мj к.
Составим уравнение мощностей, учитывая, что подводимая к колесу через крутящий момент мощность расходуется на преодоление сопротивления качению колеса, создание тяговой силы и разгон колеса
Nк = Nf + Nт+ Nj к , (3.4)
где Nк – мощность, подводимая к колесу, равная Nк=Мк×wк;
Nт – тяговая мощность, равная Nт = Рт× V;
Мощности Nf = Pf×V и Nj к= Jк 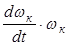 , что следует из вышеприведенного.
, что следует из вышеприведенного.
После подстановки этих значений в уравнение (3.4) и деления уравнения на скорость V, получим уравнение сил, действующих на ведущее колесо
Рк = Рf + Pт + 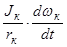 . (3.5)
. (3.5)
Если движение колеса равномерное, тогда 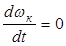 , и уравнение (3.5) примет вид Pк = Рf + Pт . (3.6)
, и уравнение (3.5) примет вид Pк = Рf + Pт . (3.6)
Из уравнения (3.6) имеем
Рт = Рк - Рf . (3.7)
Из анализа уравнения (3.7) следует, что тяговая сила зависит от свойств опорной поверхности и всегда меньше окружной силы, которая создается крутящим моментом двигателя.
Из анализа рис.3.4 видно, что окружная сила Рк и сила сопротивления качению Рf имеют противоположные направления. Их результирующая в точке А контакта колеса с дорогой Рк – Рf будет ограничена силой сцепления колеса с дорогой, равной j ×Rz ( j - коэффициент сцепления шины с опорной поверхностью). Следовательно, максимальное значение тяговой силы ограничено сцепными возможностями колеса с опорной поверхностью и определяется по формуле PT max = j ×Rz..
Тогда максимальная окружная сила, создаваемая крутящим моментом двигателя, которая ограничена сцепными возможностями шины, запишется
Рк max = Pт max + Pf = (j +f )×Rz .
 Тормозное колесо
Тормозное колесо
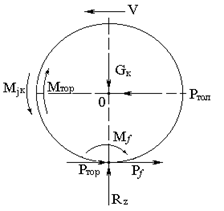
Расчетная схема сил, действующих на тормозное колесо, приведена на рис.3.5. На тормозное колесо действует тормозной момент Мтор, который вызывает тангенциальные реакции опорной поверхности. Равнодействующую этих реакций принято называть тормозной силой, равной 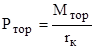
 .
.
Рис. 3.5 Тормозное колесо
Инерционный момент Мjк в этом случае будет действовать по ходу движения колеса вперед, а толкающая сила Ртол со стороны автомобиля будет направлена по вектору скорости.
С учетом направления сил уравнение мощностей, действующих на тормозное колесо, запишется Nтор + Nf = Nтол + Njк, (3.8)
где Nтор – мощность, создаваемая тормозным моментом, которая определяется по формуле Nтор= Мтор×wк = 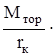 rк×wк = Ртор×V;
rк×wк = Ртор×V;
Nтол – мощность, создаваемая толкающей силой, приложенной к центру колеса
Nтол = Ртол×V;
Njк – мощность, создаваемая инерционным моментом колеса
Nj к = 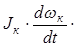 wк. После подставки этих значений в уравнение (3.8) и делением на V его правой и левой частей, получим уравнение сил, действующих на тормозное колесо Ртор + Рf = Pтол +
wк. После подставки этих значений в уравнение (3.8) и делением на V его правой и левой частей, получим уравнение сил, действующих на тормозное колесо Ртор + Рf = Pтол + 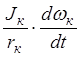 .
.
Литература
1.Гришкевия А.И. Автомобили: Теория.-Минск: Вышэйш. Шк., 1986.-240с., с.-10…26.
2. Литвинов А.С., Фаробин Я.Е. Автомобиль: Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-21-38.
4. Характеристика источника энергии
Источником энергии на автомобиле является двигатель внутреннего сгорания (ДВС): карбюраторный, инжекторный или дизельный. Принципиальное различие в работе этих двигателей заключается в том, что в карбюраторном и инжекторном двигателях воспламенение горючей смеси происходит от энергии электрической искры, а в дизеле – от температуры сжатого воздуха.
В общем случае ДВС характеризуются энергоемкостью, динамичностью и экономичностью. Энергоемкость определяется зависимостью мощности двигателя Ne от угловой скорости вращения коленчатого вала wе. Динамичность описывается зависимостью крутящего момента двигателя Ме, от угловой скорости коленчатого вала wе. Экономичность определяется зависимостью удельного расхода топлива qе от угловой скорости коленчатого вала двигателя wе.
Основной характеристикой двигателя является его внешняя скоростная характеристика – графики зависимости мощности Ne, крутящего момента Ме, удельного расхода топлива qе от угловой скорости коленчатого вала wе при максимальной подаче топлива. Эта характеристика двигателя и описывает его энергоемкость, динамичность и топливную экономичность.
Внешняя скоростная характеристика вновь созданного двигателя определяется экспериментально на заводах по производству двигателей. Эту характеристику двигателей постоянно контролируют в процессе прозводства, определяя ее экспериментально на стендах выборочно из партии произведенных двигателей.
Внешняя скоростная характеристика двигателя представлена на рис.4.1
Выделим следующие характерные точки на этой характеристике:
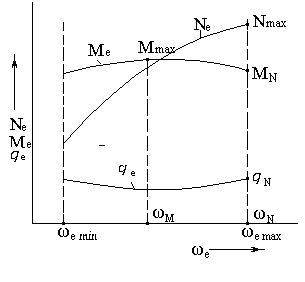 Nmax – максимальная мощность двигателя (кВт);
Nmax – максимальная мощность двигателя (кВт);
wN – угловая скорость в рад/с, соответствующая максимальной мощности двигателя ( рад./с);
Мmax – максимальный крутящий момент двигателя (Нм);
wМ – угловая скорость, соответствующая максимальному крутящему моменту (рад./с);
МN – момент, соответствующий
максимальной мощности двигателя (Нм);
qN – удельный расход топлива в г/кВт×ч, соответствующий максимальной мощности.
Рис. 4.1 Внешняя скоростная характеристика двигателя
Введем два экспериментальных коэффициента, которые определяются из внешней скоростной характеристики двигателя,
кМ = 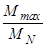 - коэффициент приспосабливаемости по моменту;
- коэффициент приспосабливаемости по моменту;
кw = 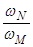 - коэффициент приспосабливаемости по частоте.
- коэффициент приспосабливаемости по частоте.
Для двигателей, применяемых на автомобилях, значения этих коэффициентов находятся в пределах км= 1,05…1,5 и кw = 1,5…2,5.
Для практических расчетов зависимости Ne= f (we) и Mе= f (we) математически описываются параболами третьего и второго порядков
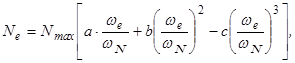 (4.1)
(4.1)
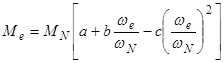 . (4.2)
. (4.2)
Неизвестными величинами в формулах (4.1) и (4.2) являются коэффициенты а, b, c.
Определим эти коэффициенты, рассмотрев режимы работы двигателя при wе=wN ,we=wM, а также исследовав функцию Ме= f (we) на экстремум.
Если зададим угловую скорость двигателя we=wN, тогда мощность, развиваемая двигателем, достигает максимального значения Ne=Nmax .
После подстановки этих условий в уравнение (4.1), имеем
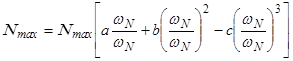 . (4.3)
. (4.3)
После сокращений получим 1 = а + b – c.
Если зададим угловую скорость двигателя we=wM, тогда крутящий момент двигателя достигнет максимального значения Ме = Мmax.
После подстановки этих условий в уравнение (4.2) имеем
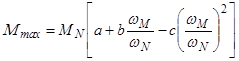 ,
,
или 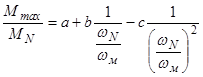 .
.
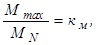 После преобразований, учитывая, что
После преобразований, учитывая, что 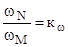
имеем 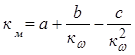 . (4.4)
. (4.4)
Для получения третьего уравнения, необходимого для определения коэффициентов а, b, c, исследуем уравнение (4.2) на экстремум.
Для чего приравняем 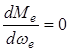 .
.
Взяв производную с уравнения (4.2), получим
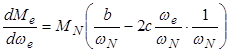 .
.
Если 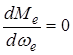 , тогда wе =wм, поскольку при этой угловой скорости вращения коленчатого вала крутящий момент двигателя достигает максимума. После подстановки и элементарных преобразований имеем
, тогда wе =wм, поскольку при этой угловой скорости вращения коленчатого вала крутящий момент двигателя достигает максимума. После подстановки и элементарных преобразований имеем
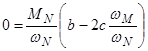 .
.
Условие выше приведенной зависимости будет выполняться, если 
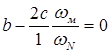 , или
, или 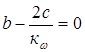 . (4.5)
. (4.5)
В результате приведенных исследований получена система из трех уравнений с тремя неизвестными а,b,c.
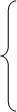 а + b – c = 1
а + b – c = 1
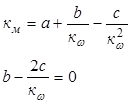 (4.6)
(4.6)
Решая эту систему, получим
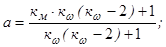
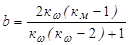 ,
, 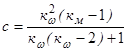 . (4.7)
. (4.7)
Поскольку входящие в уравнения (4.7) коэффициенты кw и км являются экспериментальными, поэтому и коэффициенты а,b,c также являются экспериментальными. На заводах по производству двигателей экспериментально определяется внешняя скоростная характеристика, а затем по этой характеристике с учетом зависимостей (4.7) рассчитываются коэффициенты а,b,c. Каждый тип двигателей имеет характерные только для него значения коэффициентов а,b,c. Эти коэффициенты представлены в справочной литературе.
Для определения удельного расхода топлива в зависимости от угловой скорости коленчатого вала wе рекомендуется воспользоваться эмпирической зависимостью
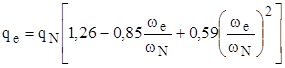 ,
,
где qN – удельный расход топлива при максимальной мощности в г/кВт×ч, который для дизельных двигателей принимается 210¸240 г/кВт×ч, а для карбюраторных двигателей - 310¸340 г/кВт×ч.
В табл. 4.1 приведены значения параметров двигателей.
Таблица 4.1 Параметры карбюраторных и дизельных двигателей
| Марка | Vл ,л | Тип | Nemax, кВт | 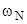 ,
рад/с ,
рад/с
| Меmax, Н.м | Км | 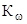
| Коэффициенты | ||
| а | b | с | ||||||||
| ВАЗ-2103 ВАЗ-2106 ВАЗ-2108 М-412 ЗМЗ-24Д ЗМЗ-66 ЗИЛ-130 ЗИЛ-375 КамАЗ-740 ЯМЗ-236 ЯМЗ-238 ЯМЗ-238Н ЯМЗ-240 | 1,45 1,57 1,3 1,48 2,445 4,25 6,00 7,00 10,85 11,15 14,86 14,86 22,30 | К4Р К4Р К4Р К4Р К4Р К8V К8V K8V Д8V Д6V Д8V Д8V Д12V | 56,6 58,8 48,8 55,2 69,9 84,6 110,3 132,4 154,6 132,4 176,5 220,6 264,8 | 586,4 565,5 586 607,4 471,2 345,4 335,1 335,1 272,2 219,9 219,9 219,9 219,9 | 105,1 121,6 95,2 111,2 186,3 284,4 402,0 465,0 637,6 666,7 882,6 1078,7 1274,8 | 1,088 1,16 1,19 1,22 1,26 1,16 1,22 1,18 1,12 1,107 1,099 1,075 1,061 | 1,6 1,8 1,19 1,8 1,87 1,47 1,68 1,68 1,6 1,4 1,4 1,4 1,4 | 0,84 0,91 0,64 0,97 0,85 0,44 0,75 0,80 0,68 0,44 0,48 0,61 0,68 | 0,78 0,9 1,75 0,98 1,46 2,12 1,59 1,3 1,38 1,87 1,73 1,31 1,07 | 0,62 0,81 1,39 0,95 1,31 1,56 1,34 1,10 1,06 1,31 1,21 0,92 0,75 |
Заметим, что приведенные выше параметры двигателей определялись на стендовом оборудовании. В реальных условиях эксплуатации на автомобиле двигатель работает с другими впускной и выпускной системами, на нем установлено дополнительное оборудование, для привода которого затрачивается дополнительная мощность. Поэтому эффективная мощность, развиваемая двигателем на автомобиле, несколько меньшая. Однако, как показал анализ литературных источников, это уменьшение не превышает 15%.
Литература
1. Гришкевич А.И. Автомобили: Теория.- Минск: Вышэйш шк.,1986.-240 с., с.-28…30.
2. Кошарний М.Ф. Основи механіки та енергетики автомобіля. -К.: Вища шк., 1992.-200 с., с. –22-30.
3. Литвинов А.С., Фаробин Я.Е. Автомобиль: Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-28-31.
Контрольные вопросы
1.Какие типы двигателей применяются на автомобилях?
2. В чем принципиальное отличие карбюраторного и инжекторного двигателей от дизельного?
3. Что такое внешняя скоростная характеристика двигателя?
4.Каким образом определяются коэффициенты приспосабливаемости двигателей по частоте и крутящему моменту?
5.Каким образом рассчитываются коэффициенты а,в,с ?
5. Тягово-скоростные свойства автомобиля
Дата добавления: 2017-06-02; просмотров: 2801;
