Оценка качества технологического процесса

Пусть элемент рассматриваемого ЭС характеризуется m функциональными параметрами 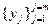. На каждый функциональный параметр y_j установлены допустимые пределы его изменения

y_{j min}=M(y_j)-e и y_{j max}=M(y_j)+e,

где M(y_j) – номинальное значение функционального параметра качества y_j;

e - абсолютная величина половины поля допуска на параметр y_j.

Практически любой функциональный параметр качества любого элемента ЭС можно выразить через физические и геометрические характеристики элемента:

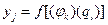
где j_k – k-я физическая характеристика элемента;

q_l – l-я геометрическая характеристика элемента.

Например, сопротивление как функциональный параметр качества резистивного элемента ЭС может быть представлено в следующем виде:

,

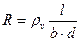где r_v-объемное удельное сопротивление резистивного элемента (физическая характеристика);

l, b, d – соответственно его длина, ширина и толщина (геометрические характеристики).

Отклонение функционального параметра качества y_j конкретного элемента ЭС от среднего значения 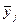или номинального значения этого параметра обусловлено соответствующими отклонениями физических и геометрических характеристик от их номинальных значений. В производственных условиях отклонения могут служит оценкой погрешностей АПЕ. Следовательно, качество каждой АПЕ многооперационного технологического процесса изготовления элементов ЭС может быть оценено систематическими Dj_k, Dq_l и случайными 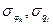погрешностями значений физических и геометрических характеристик.

Для получения коэффициента выхода годных ЭС близким единице необходимо обеспечить трехсигмовое изменение функционального параметра качества в пределах поля допуска, т.е.

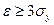
Тогда задача сводится к определению и обеспечению соответствующих погрешностей АПЕ. При этом для расчета необходимых погрешностей АПЕ можно использовать известную зависимость:

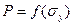, (5)

где .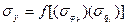

Однако в большинстве случаев реализовать условие 100% - ого выхода годных ЭС практически не удается. Поэтому на практике ставиться задача обеспечения не 100%-ого выхода годных изделий, а: P³ P_min

В этом случае с помощью формулы (5) определяют s_y, которая соответствует установленному P_min,. Далее определяем 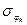и .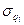

В тех случаях, когда функциональный параметр качества y_j распределен по гауссовскому закону, зависимость (5) может быть записана следующим образом:

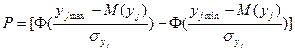, (6)

где ;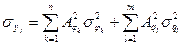

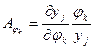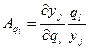; - коэффициенты весомости;

Формула (6) позволяет подготовить решение об очередности эффективной настройки АПЕ технологического процесса. При одинаковой трудоемкости настройки эффект от этого процесса будет больше в тех случаях, когда коэффициенты влияния будут больше.

Анализ ТП только по критериям точности во многих случаях является недостаточным ввиду того, что он не учитывает фактор времени (расстройка). Поэтому вводят другие показатели: понятие устойчивости и стабильности технологического процесса.