Линейного программирования.
Пусть торговое предприятие реализует n групп товаров, используя при этом ограниченные материально-денежные ресурсы размером bi 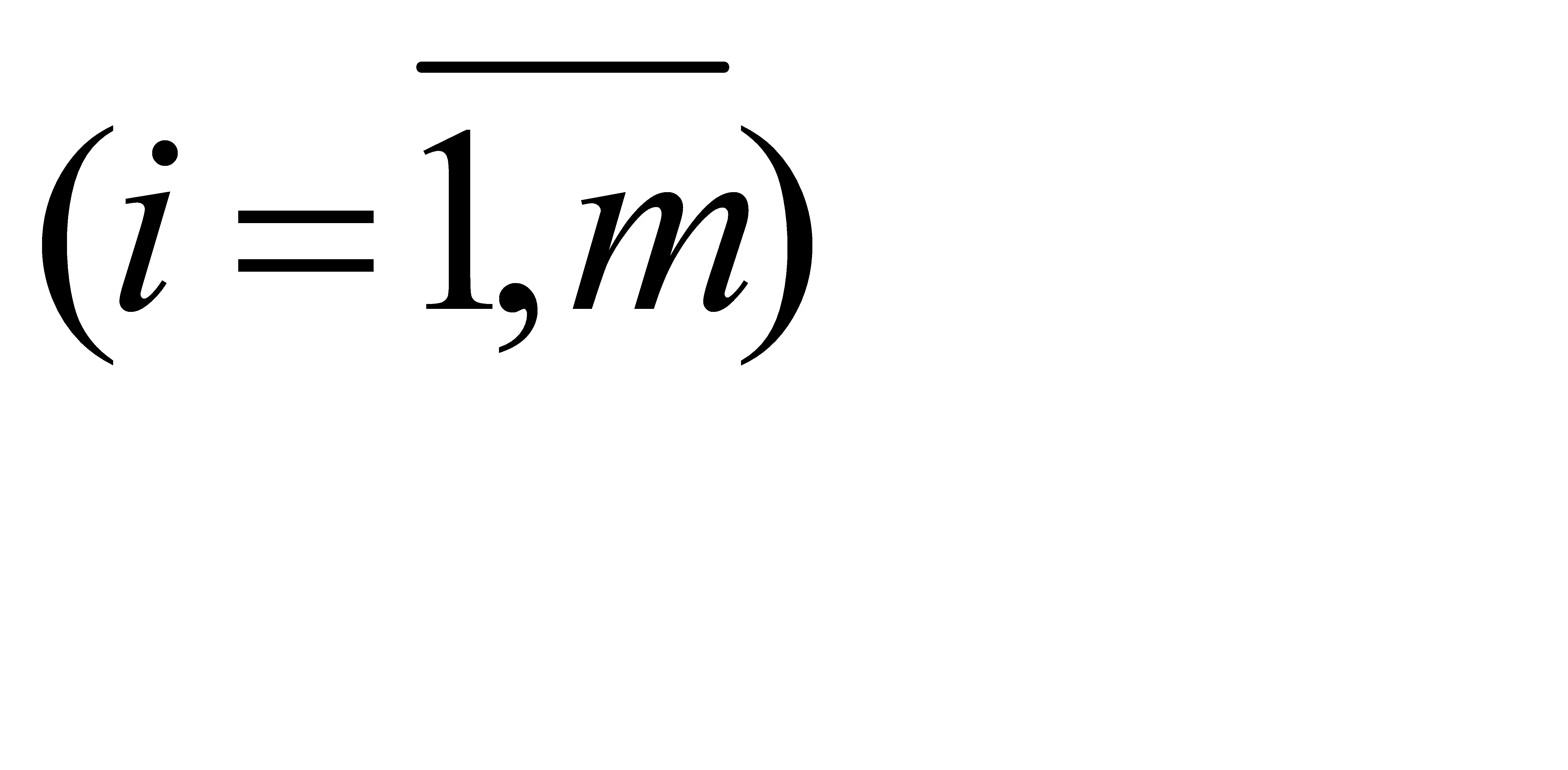 . Известны расходы ресурсов i –го вида на организацию продажи единицы товарооборота товаров j-ой группы, заданные в виде технологической матрицы А = (aij) ,
. Известны расходы ресурсов i –го вида на организацию продажи единицы товарооборота товаров j-ой группы, заданные в виде технологической матрицы А = (aij) , 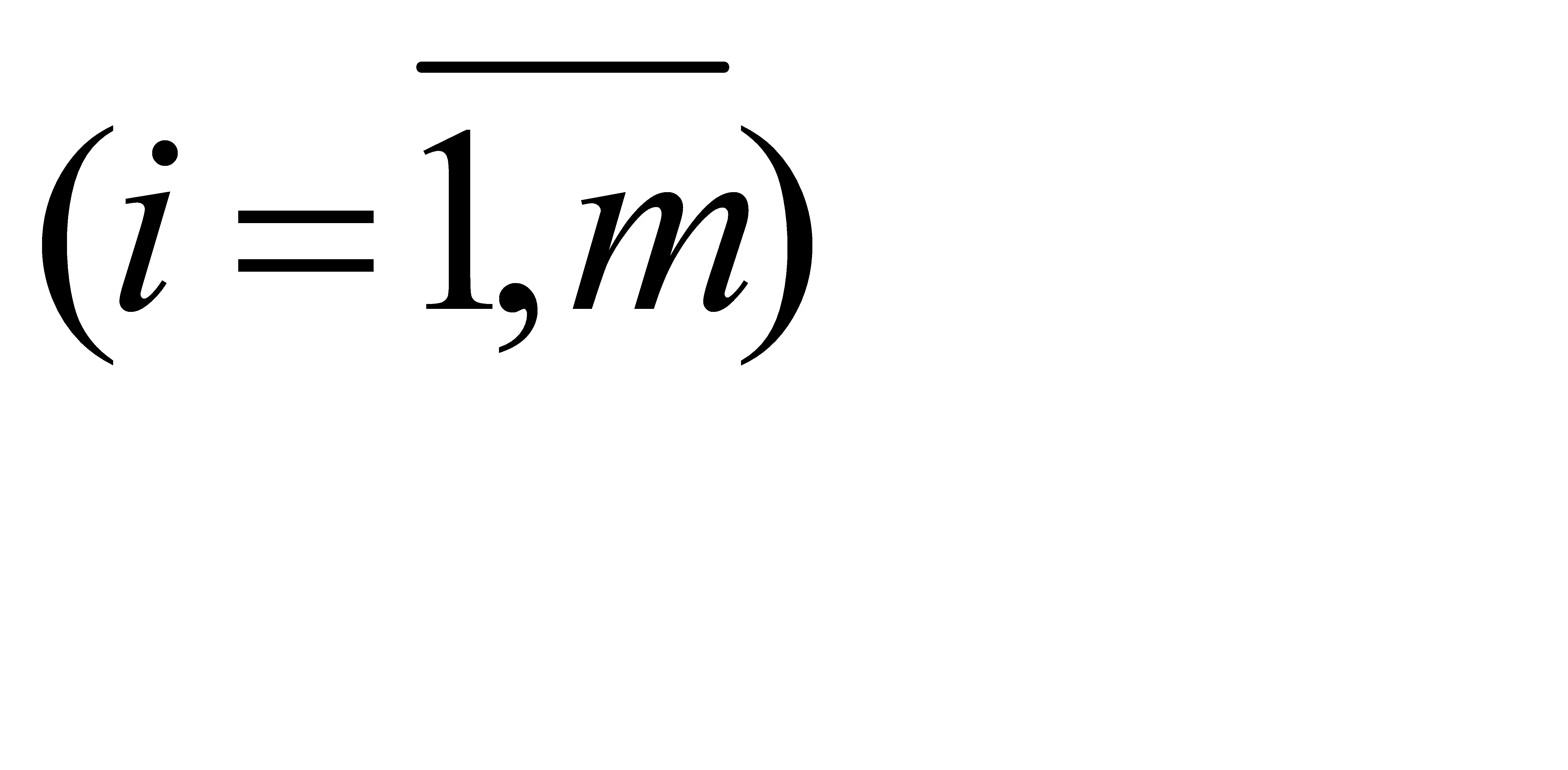 ,
, 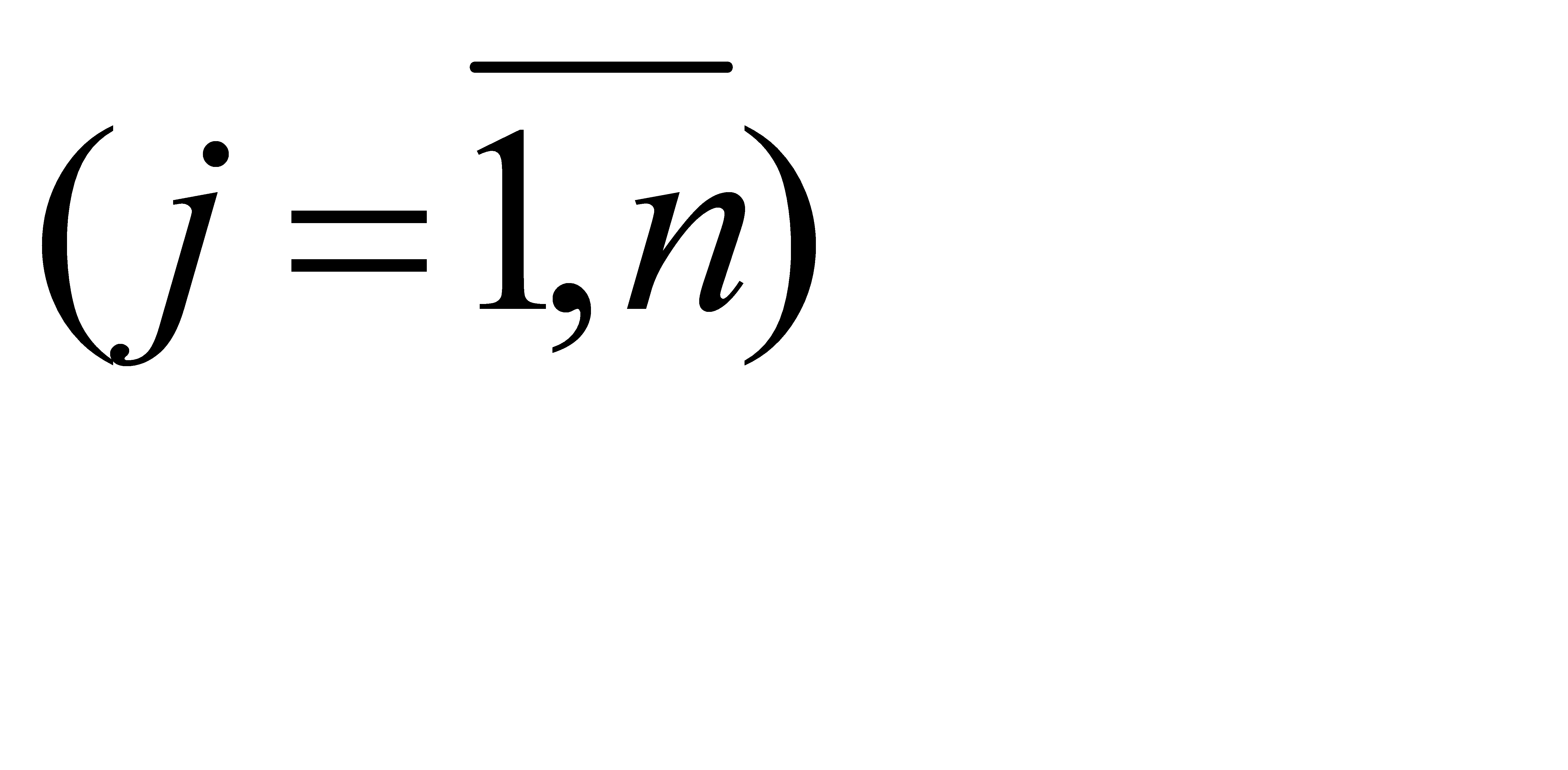 , и прибыль, получаемая предприятием от реализации единицы товарооборота товаров j-ой группы - Сj.
, и прибыль, получаемая предприятием от реализации единицы товарооборота товаров j-ой группы - Сj.
Требуется определить объем и структуру товарооборота Хj 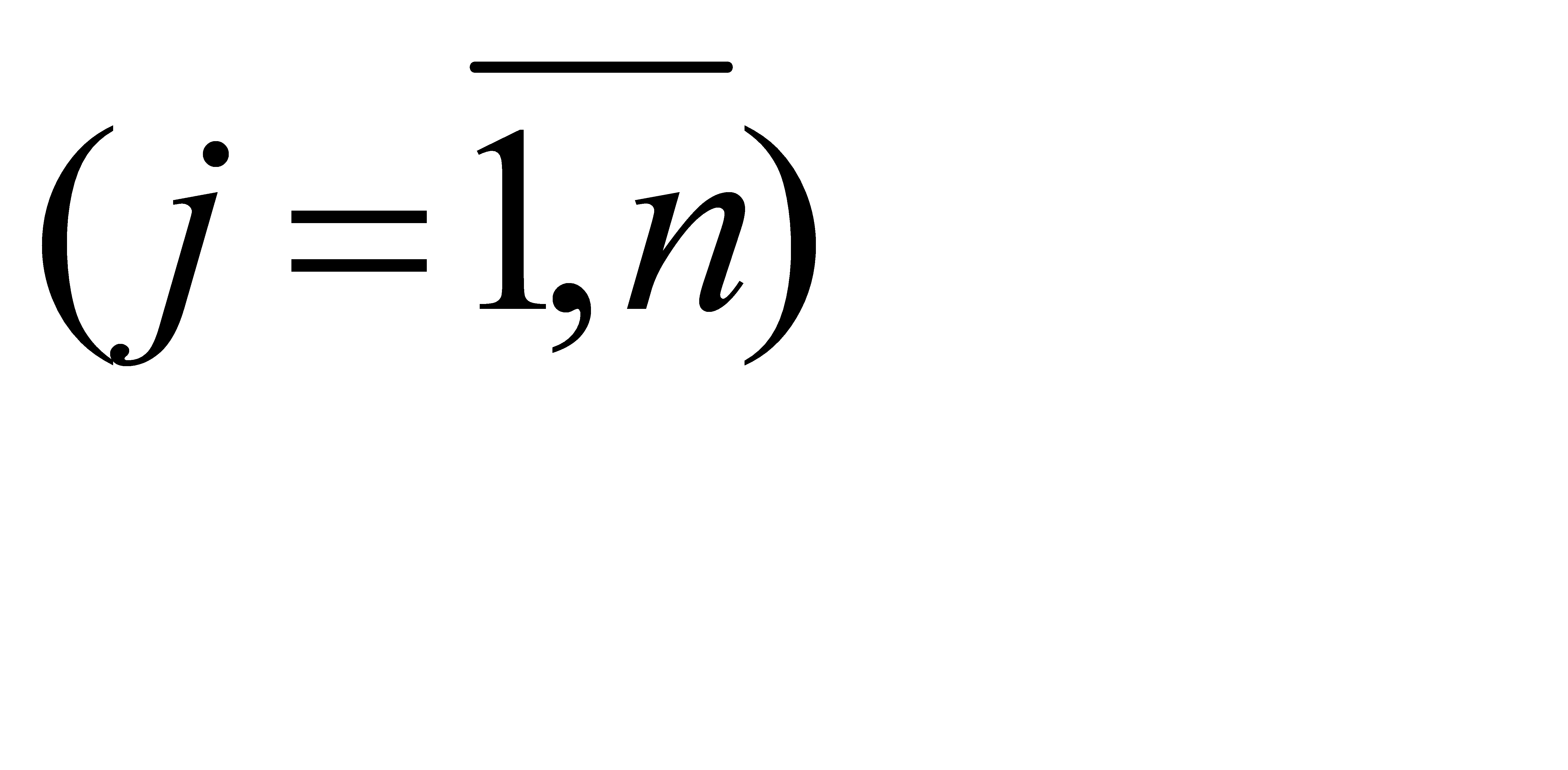 , при которых общая прибыль торгового предприятия была бы максимальной.
, при которых общая прибыль торгового предприятия была бы максимальной.
Математическую модель задачи можно записать следующим образом:
Определить 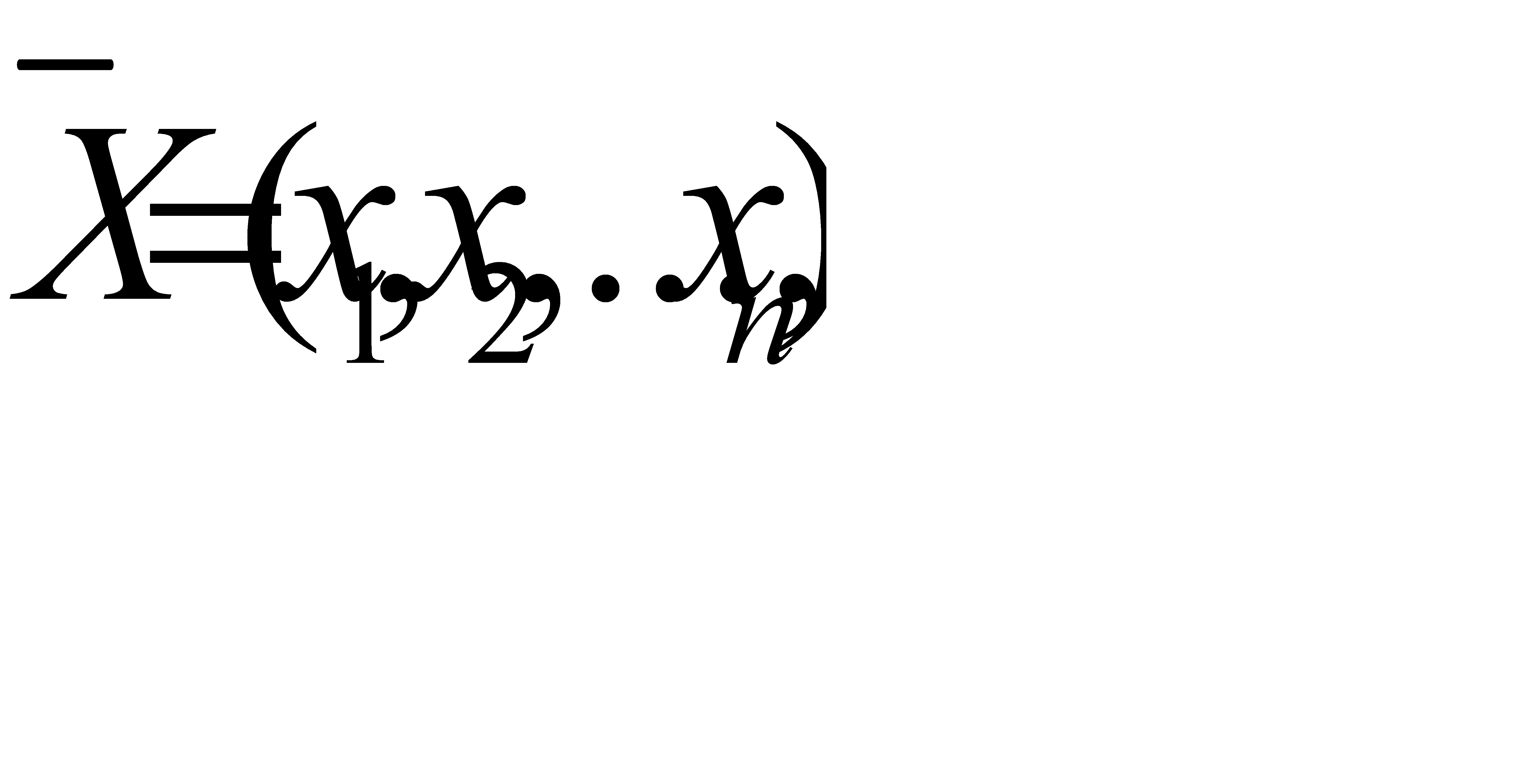 , который удовлетворяет ограничениям
, который удовлетворяет ограничениям
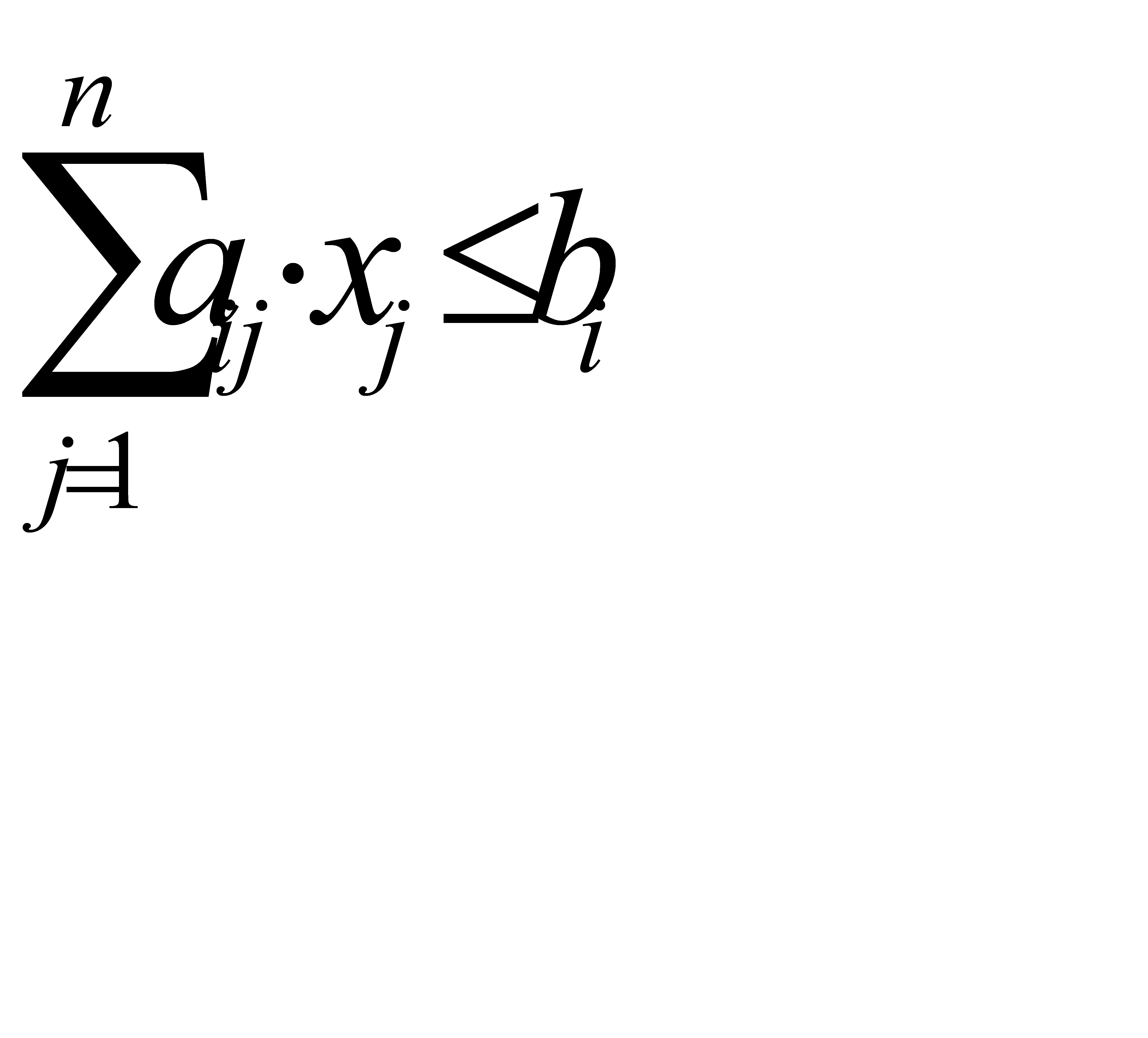 ,
, 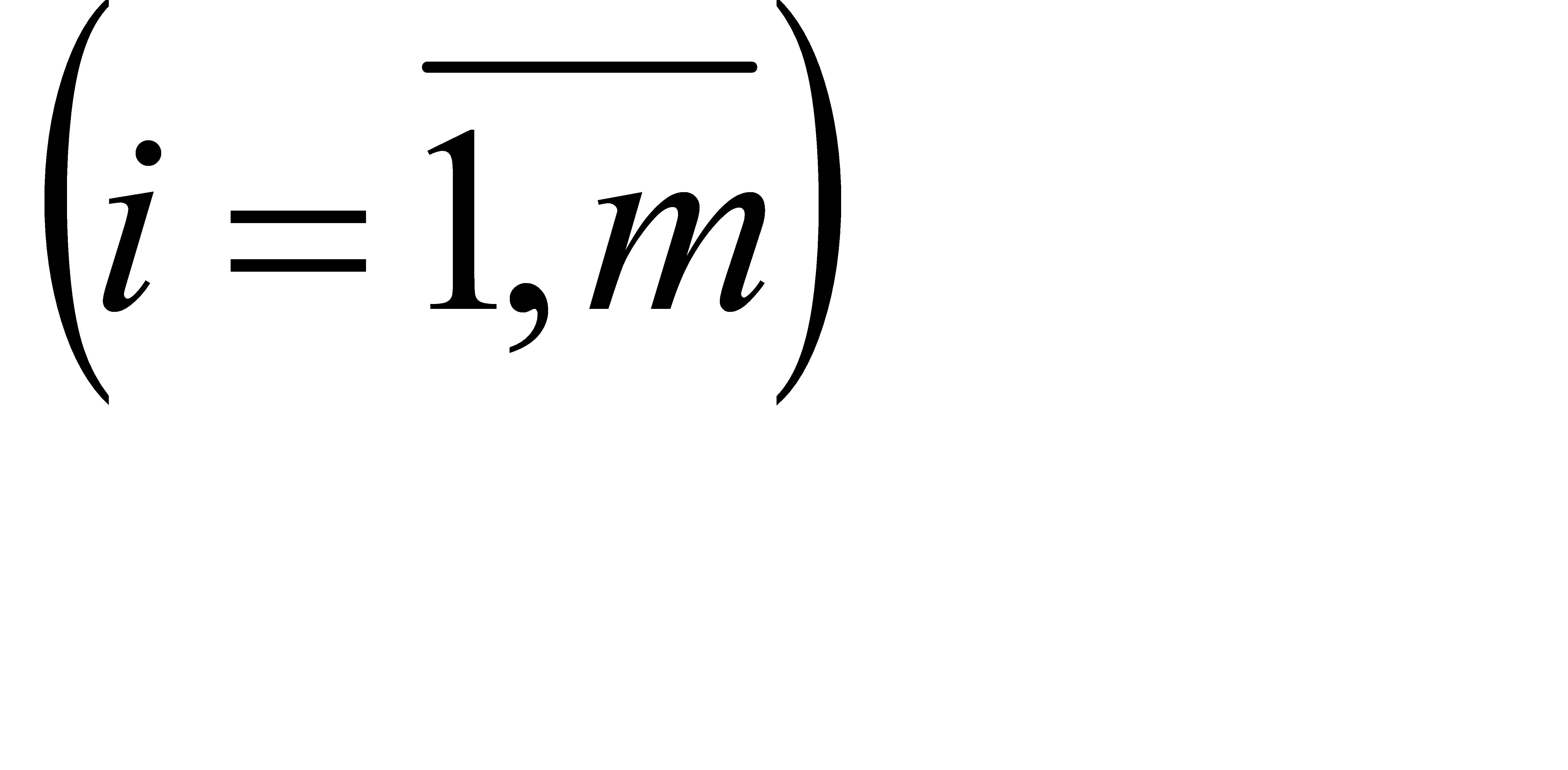 (2.1)
(2.1)
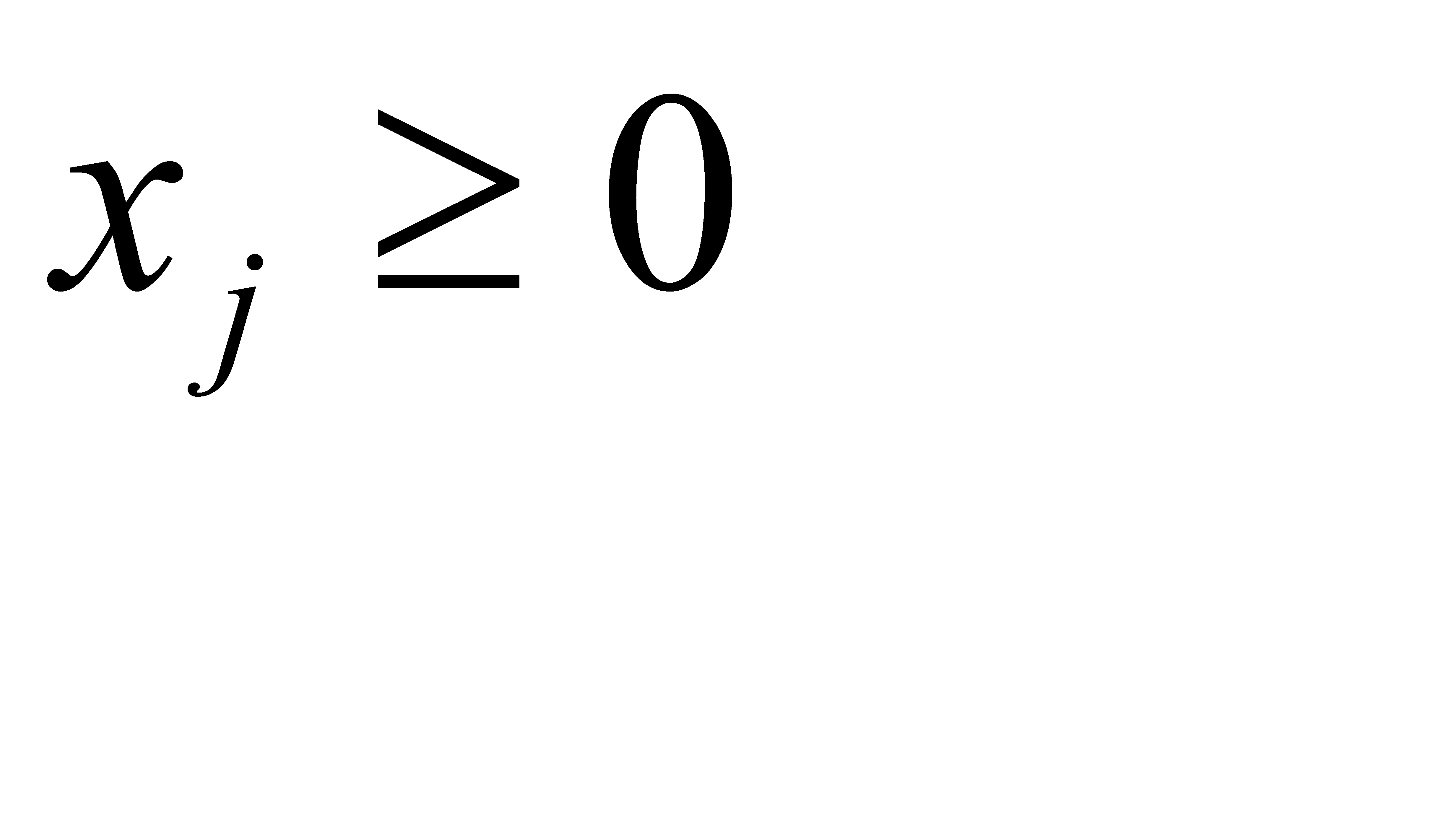 ,
, 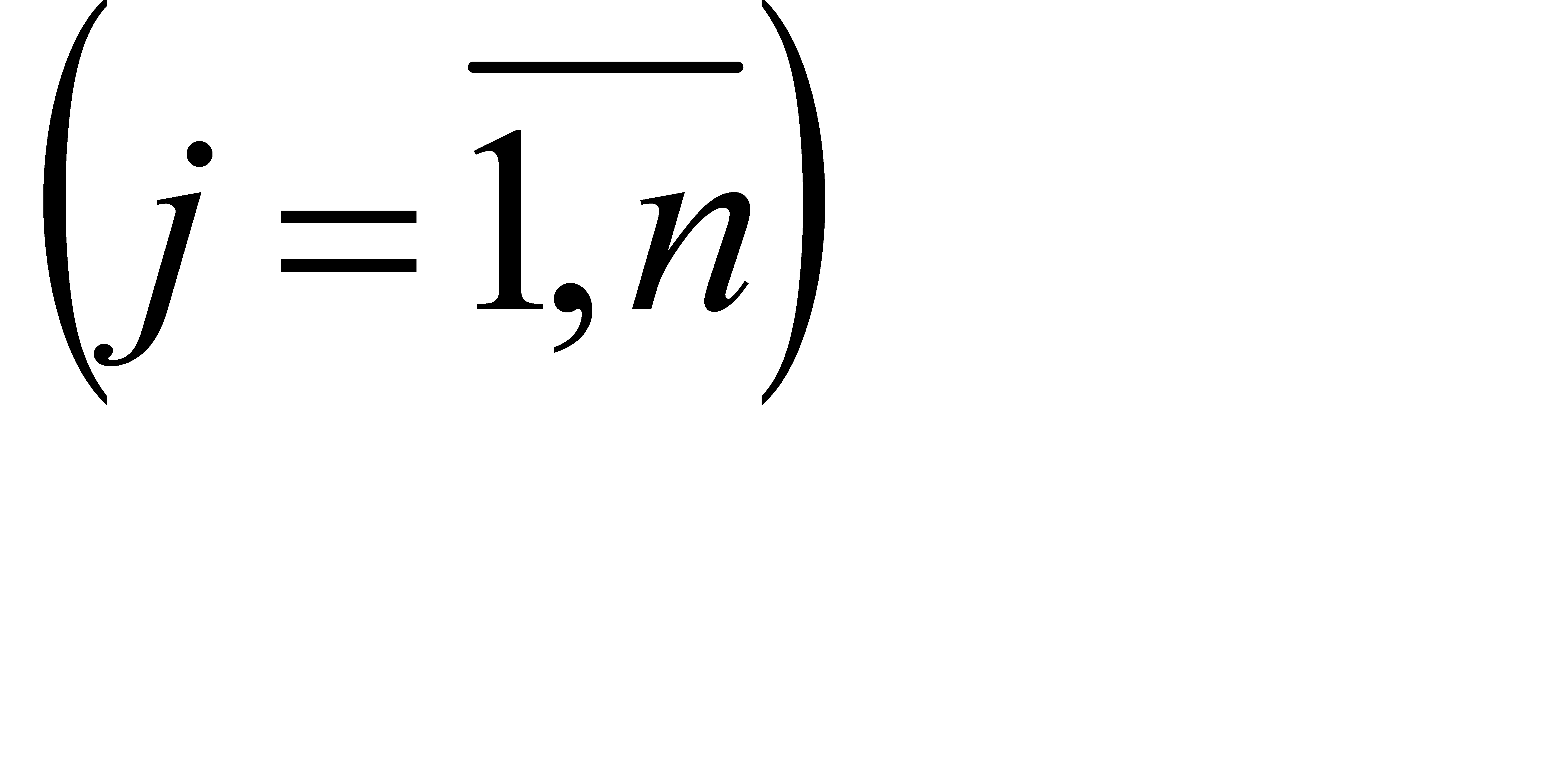 (2.2)
(2.2)
и доставляет максимальное значение целевой функции
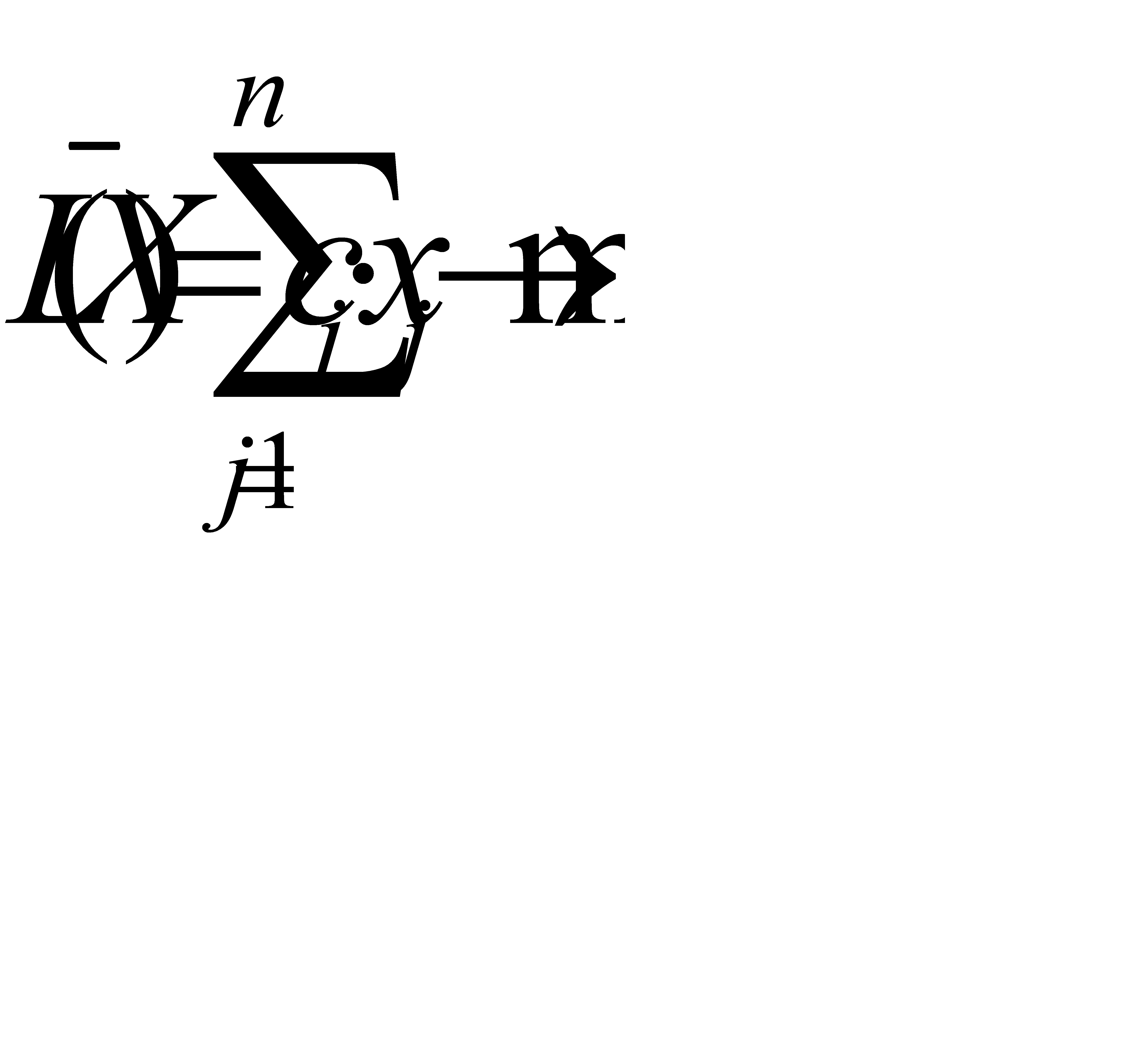 (2.3)
(2.3)
Задача линейного программирования (2.1)–(2.3) может быть решена симплексным методом, так как система ограничений задана в виде системы неравенств только смысла «≤ » и вектор столбец свободных членов содержит только положительные числа, т.е.
bi ≥ 0.
Алгоритм симплексного метода включает следующие этапы.
1. Составление первого опорного плана.
Перейдем от системы неравенств (2.1) к системе уравнений путем введения неотрицательных дополнительных переменных. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными.
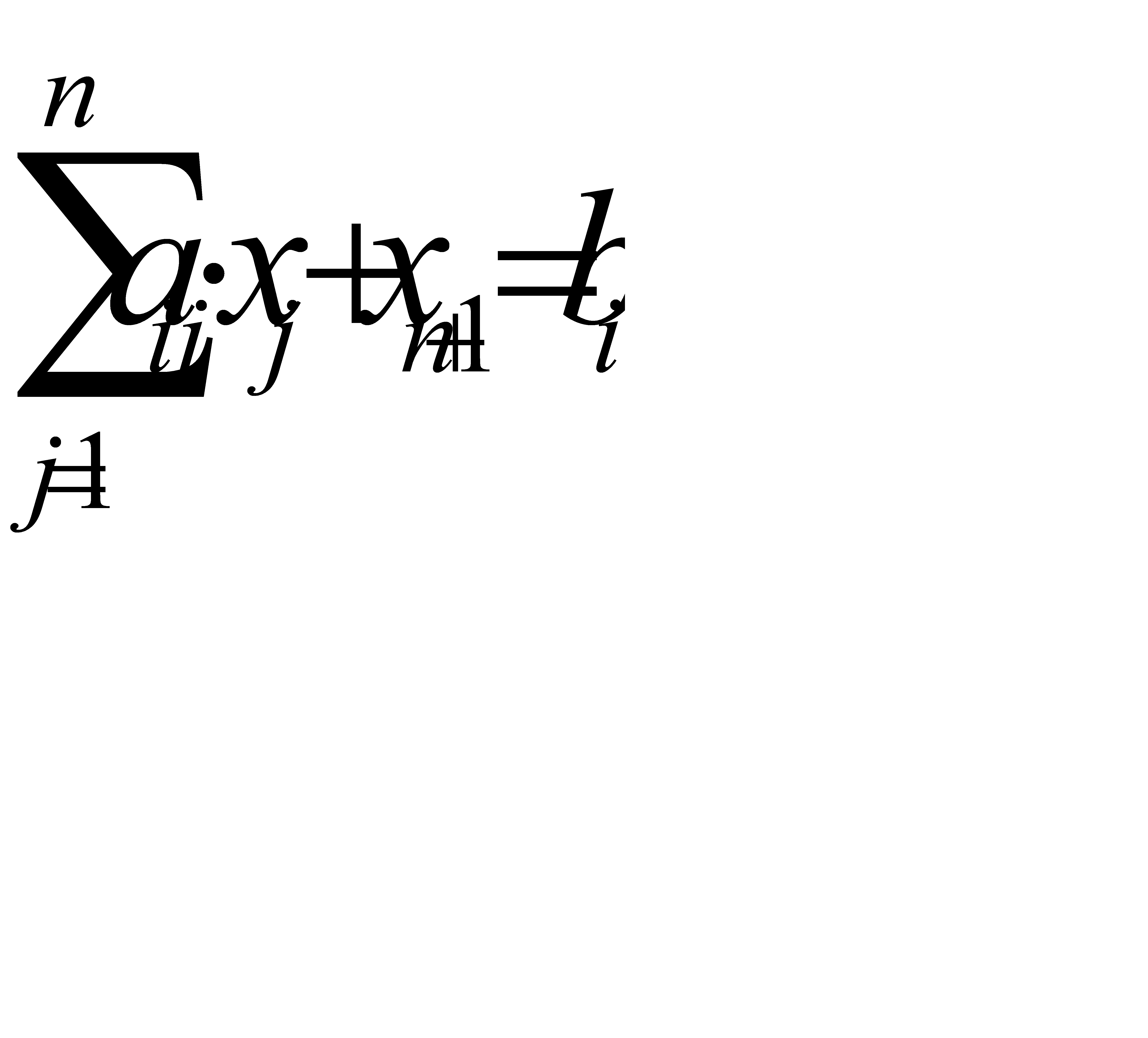 ,
, 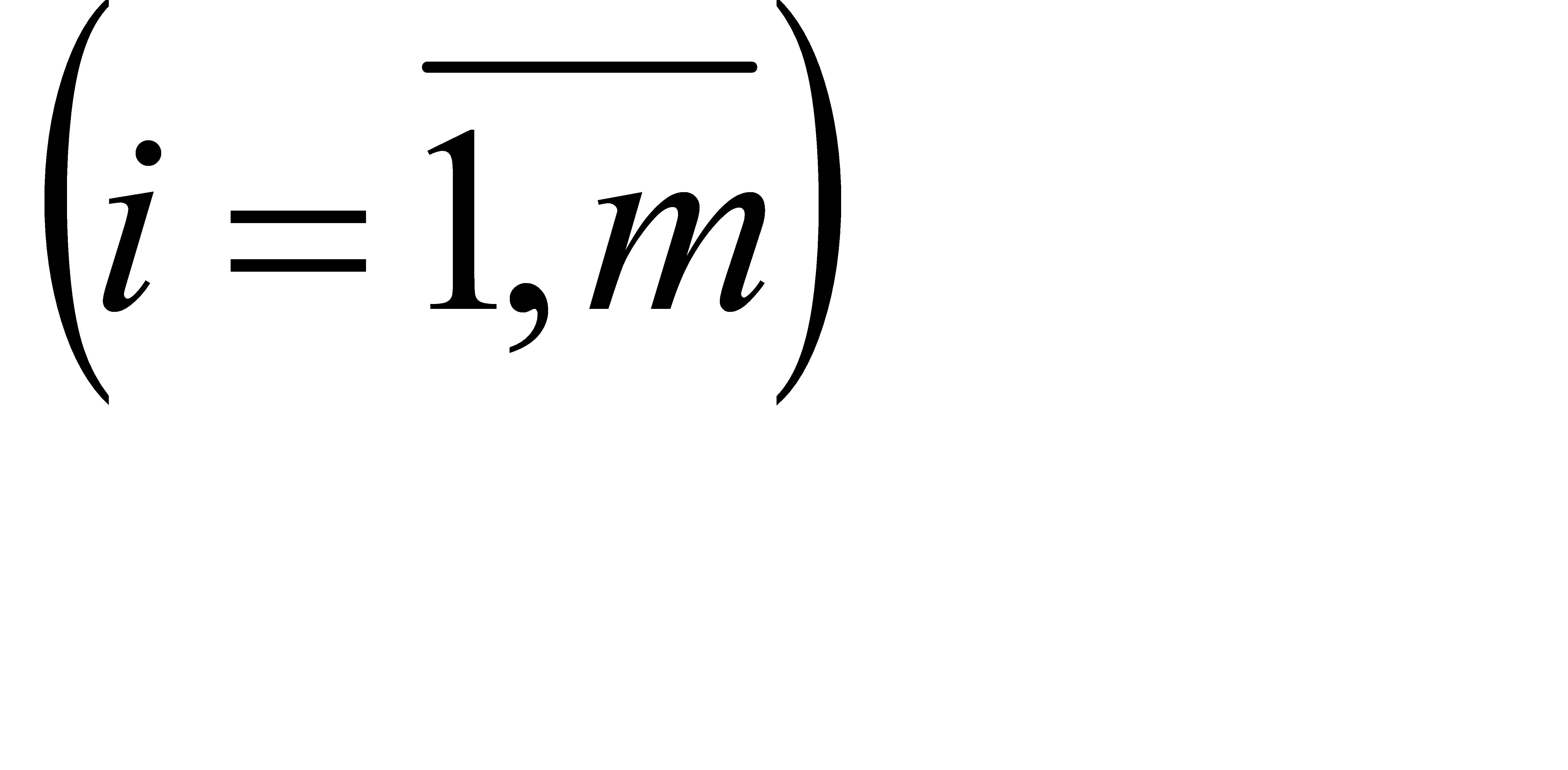 (2.4)
(2.4)
Разрешим систему уравнений (2.4) относительно базисных переменных:
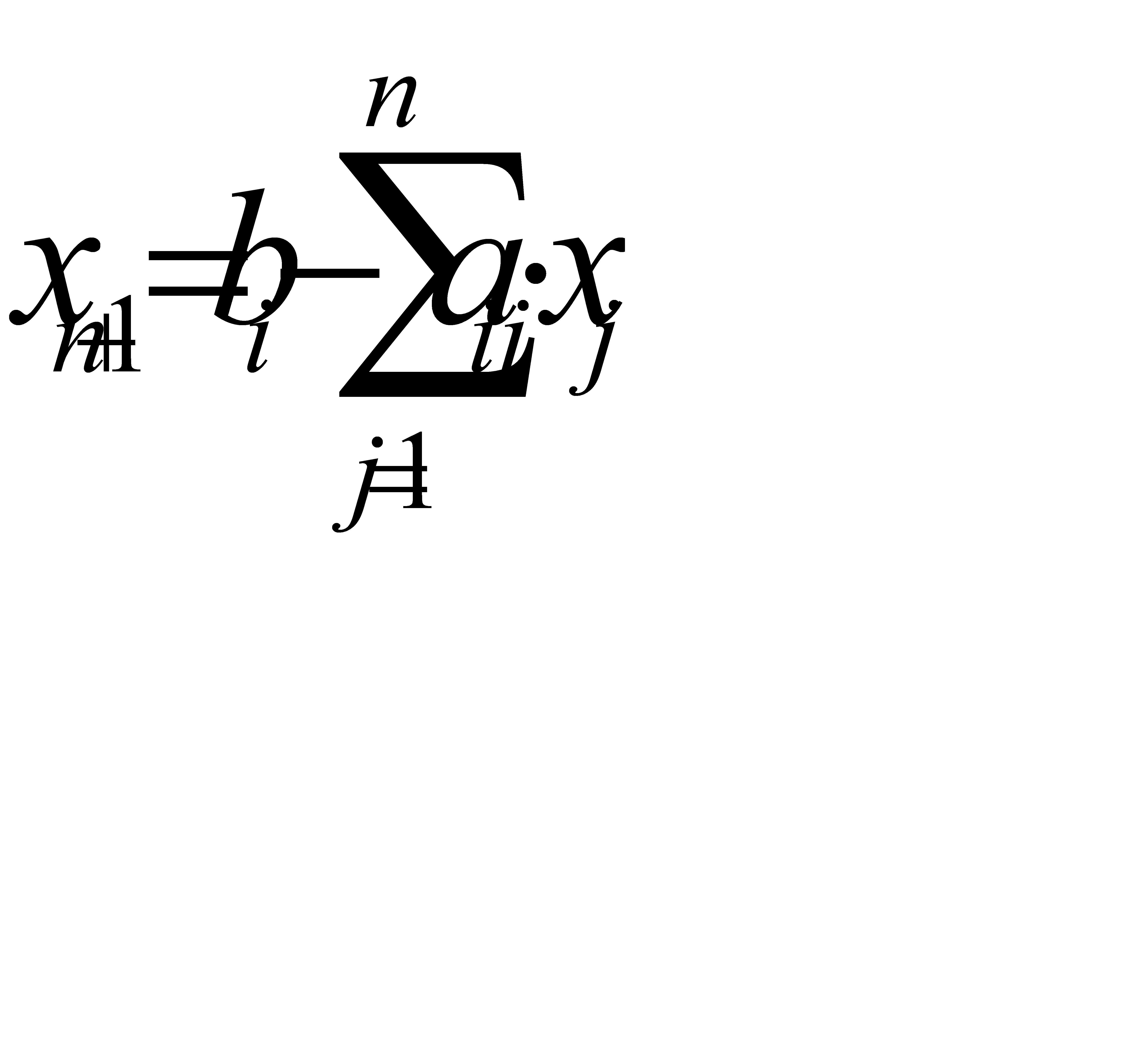 ,
, 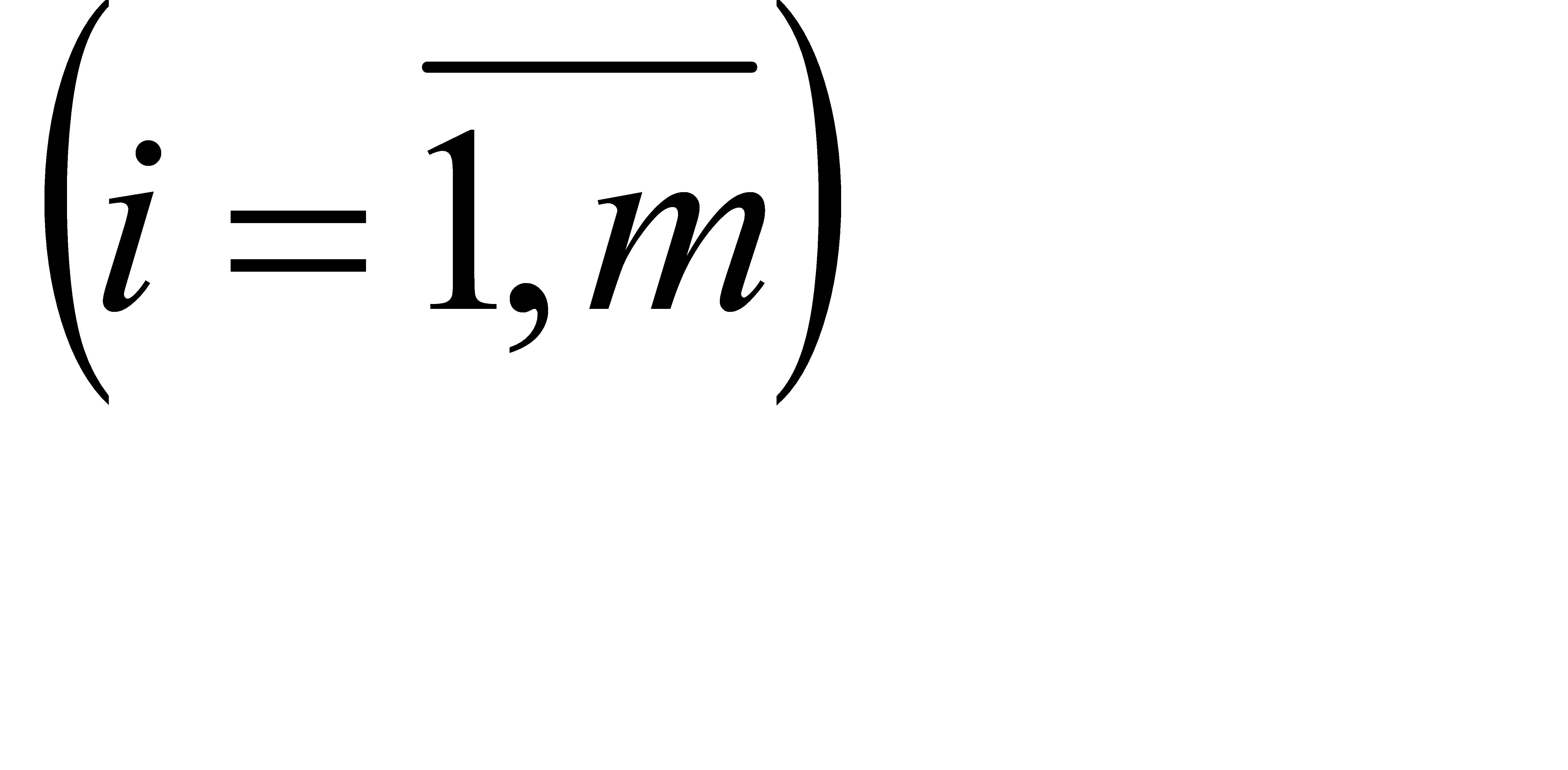 (2.5)
(2.5)
Аналогично функцию цели представим в виде:
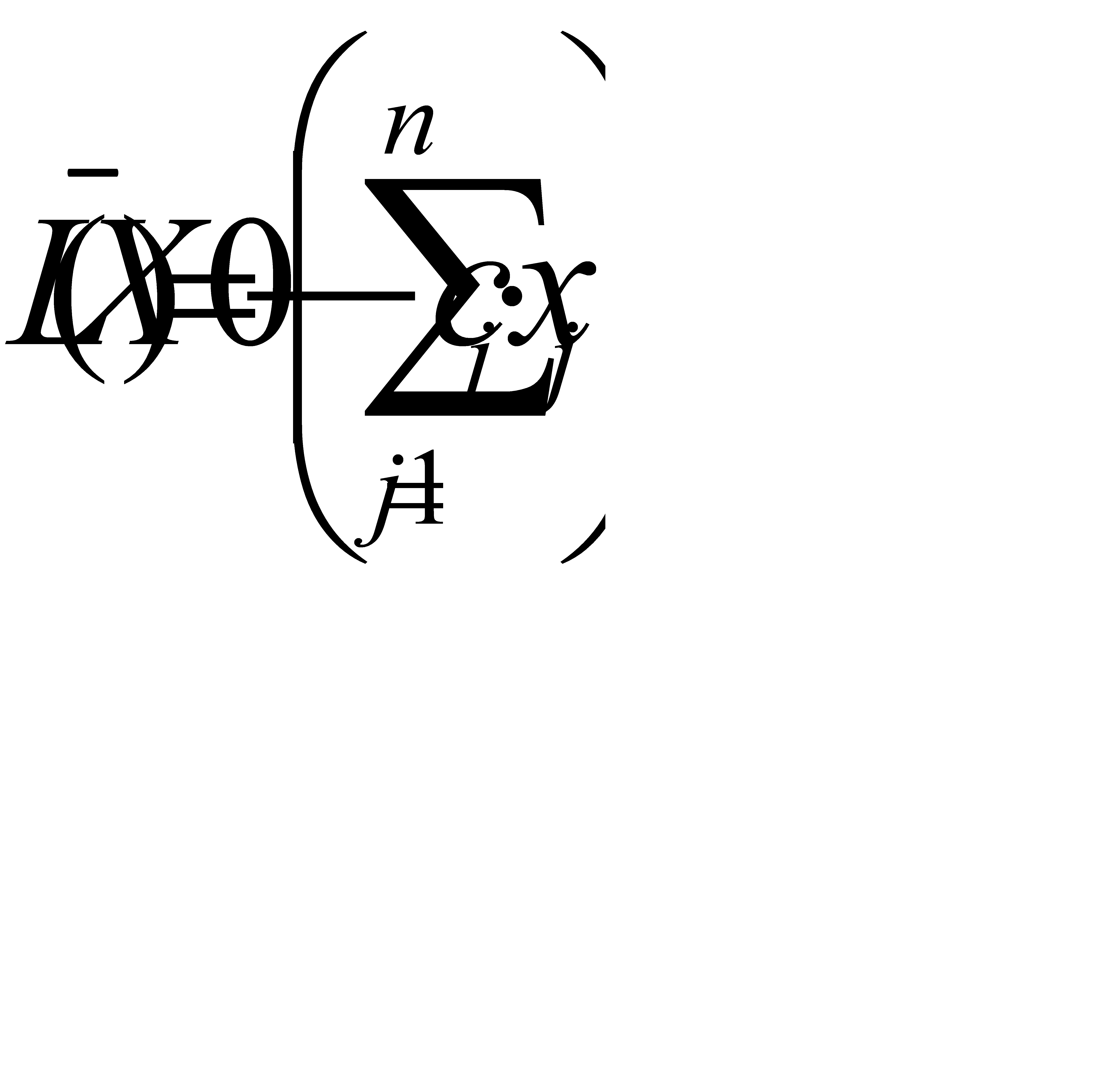 (2.6)
(2.6)
Полагая, что основные переменные 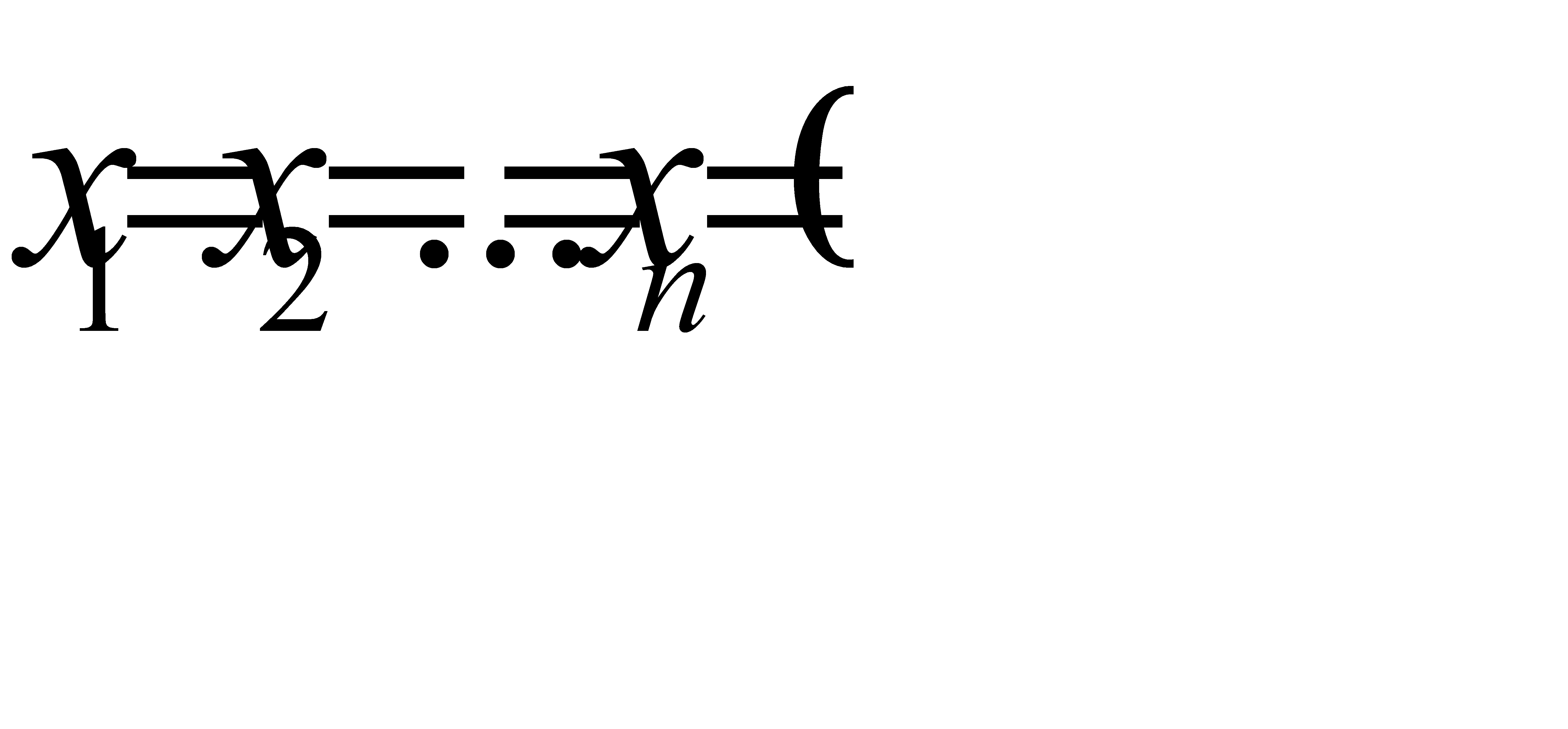 , получим первый опорный план
, получим первый опорный план 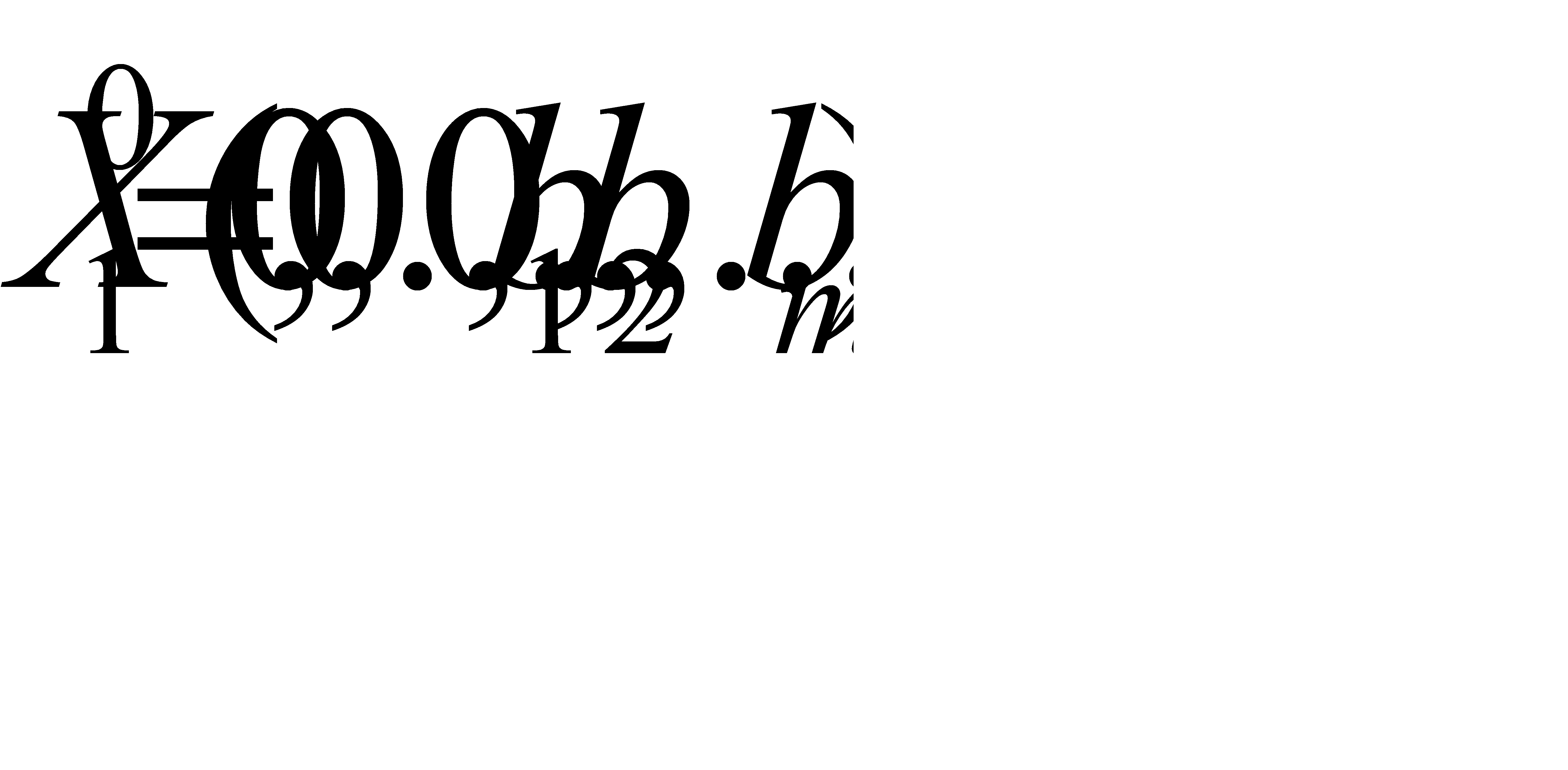 ,
, 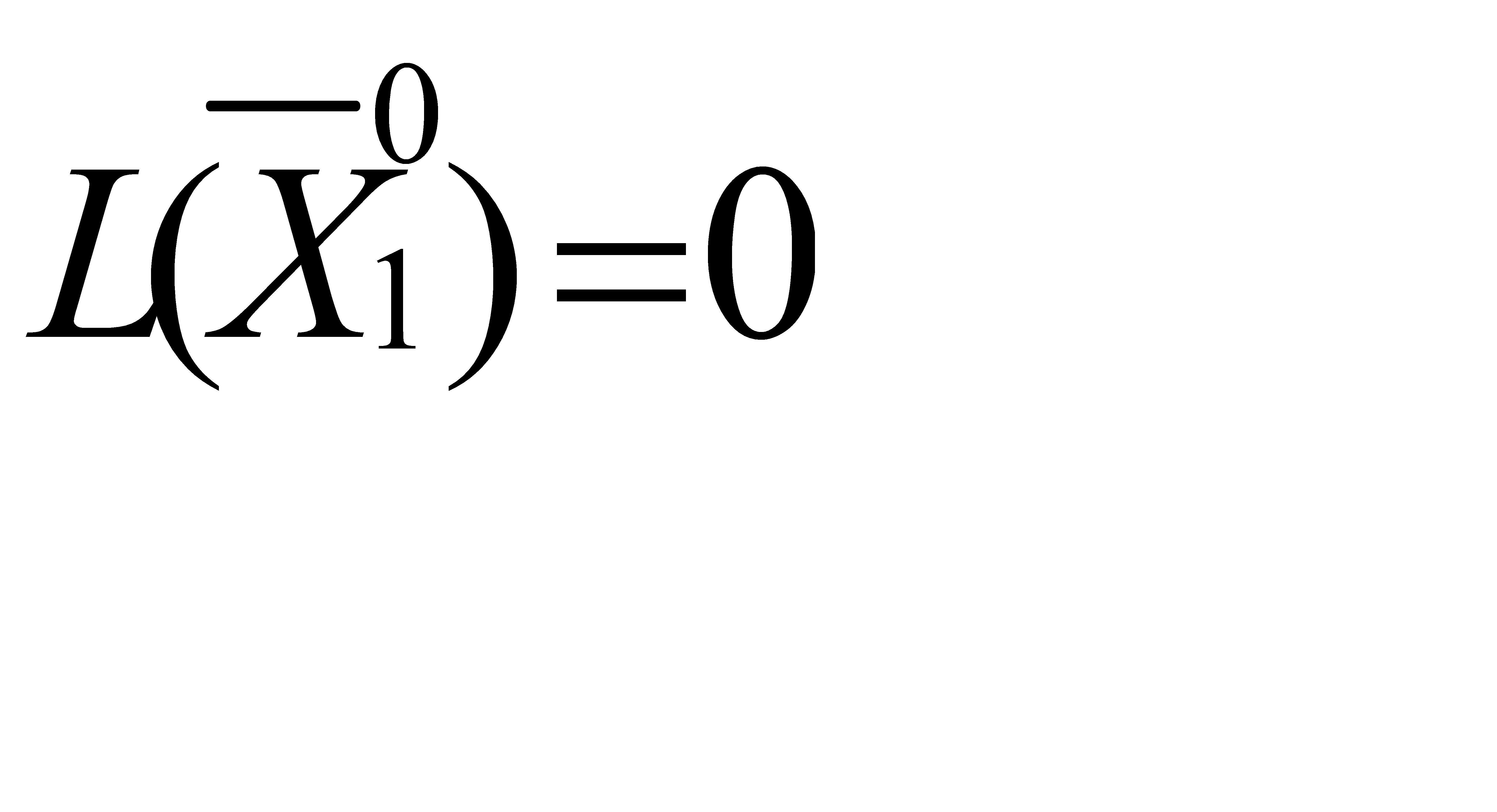 .
.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения первого опорного плана, занести в симплексную таблицу. Первые m строк симплексной таблицы содержат коэффициенты системы ограничений и свободные члены. Последняя (m +1)-ая строка таблицы называется индексной. Она заполняется коэффициентами функции цели, взятыми с противоположным знаком.
2. Проверка оптимальности опорного плана.
Если все коэффициенты индексной строки симплексной таблицы (при решении задачи на максимум целевой функции) неотрицательны (∆ ≥ 0, 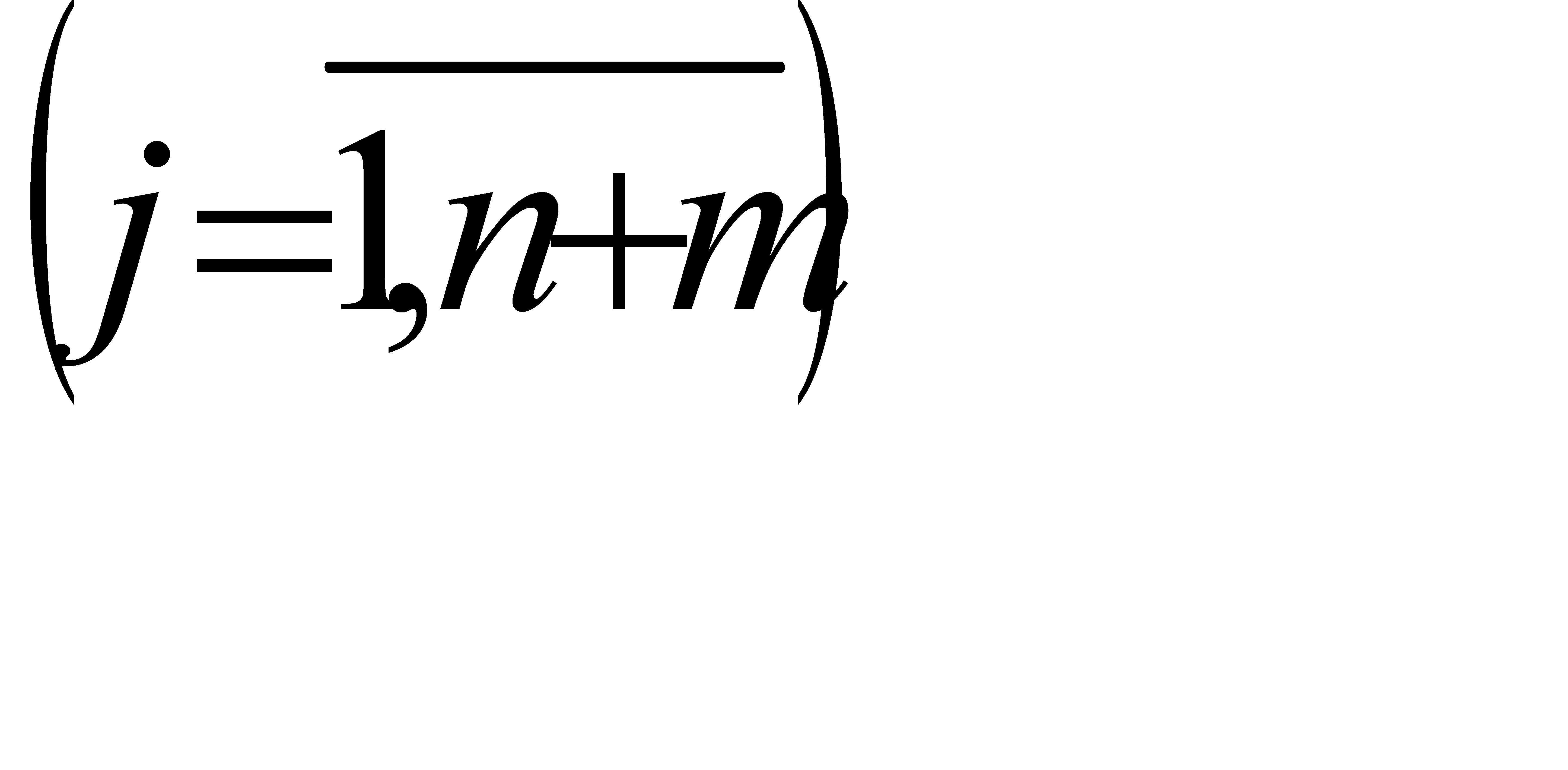 , то опорный план задачи является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, план не оптимальный и можно перейти к новому опорному плану, при котором значение целевой функции увеличится. Переход к другому плану осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора.
, то опорный план задачи является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, план не оптимальный и можно перейти к новому опорному плану, при котором значение целевой функции увеличится. Переход к другому плану осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора.
3. Определение направляющих (разрешающих) столбца и строки.
Из отрицательных коэффициентов индексной строки ∆j < 0 выбираем максимальный по абсолютной величине. Направляющий столбец, соответствующий выбранному коэффициенту, показывает, какой вектор или переменная на следующей итерации прейдет из свободных в базисные. Пусть, например, ∆k < 0 и решено ввести в базис вектор А k.
Для определения вектора (переменной), подлежащего исключению из базиса, элементы столбца свободных членов симплексной таблицы (значения базисных переменных) делим на соответствующие положительные элементы направляющего столбца 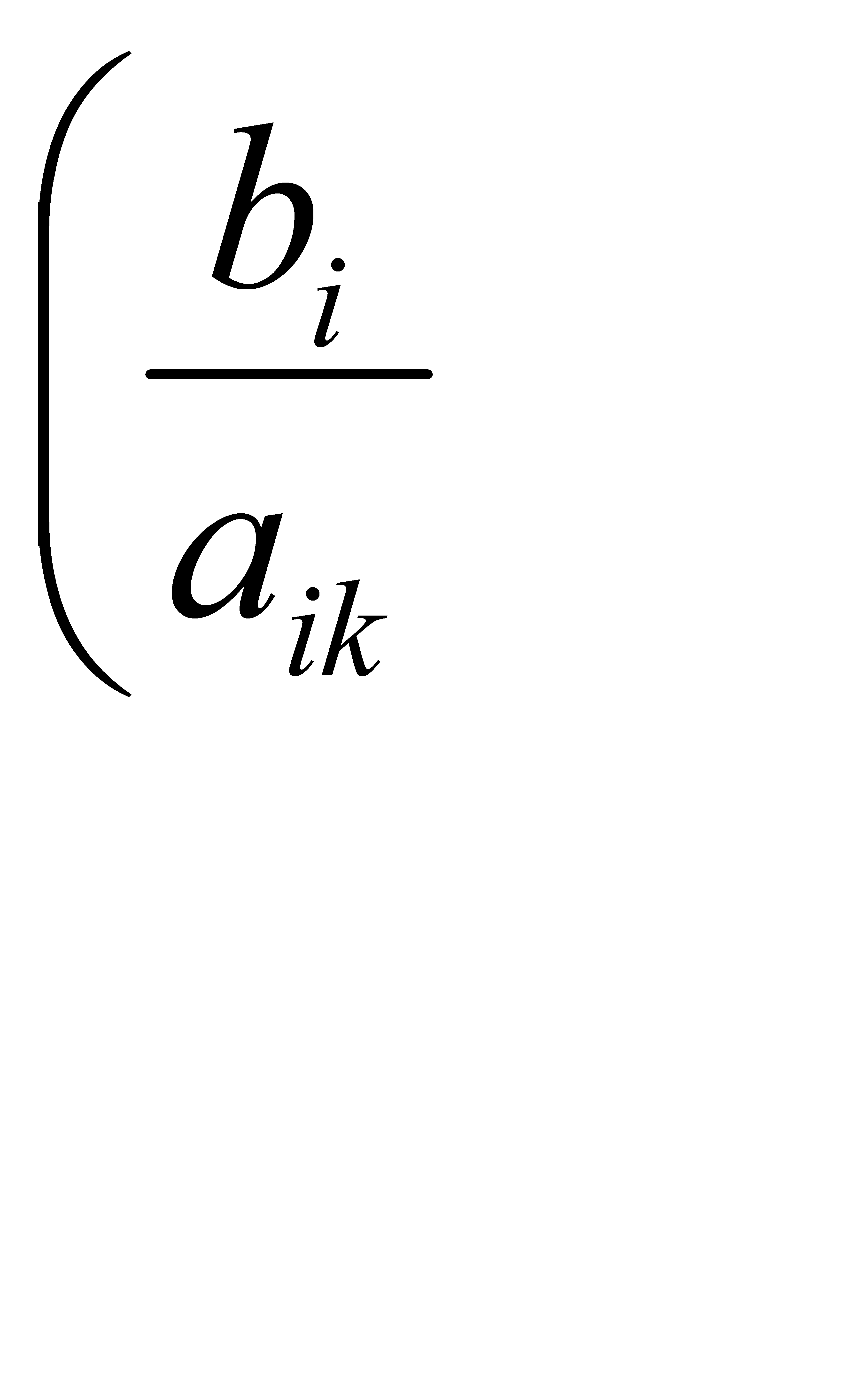 для всех
для всех 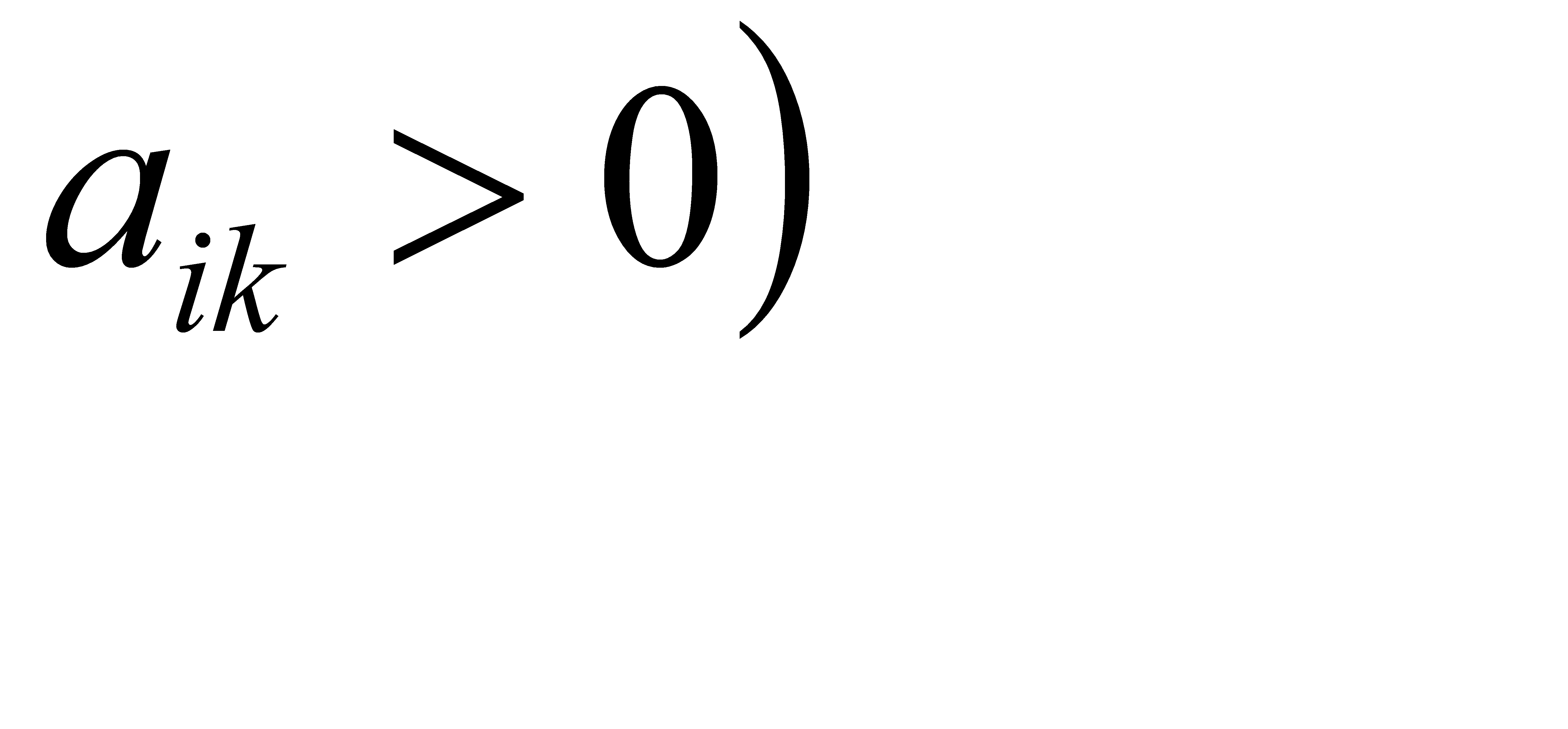 . Результаты заносим в столбец Θ симплексной таблицы. Строка симплексной таблицы, соответствующая минимальному значению Θ, является направляющей. Пусть этот минимум достигается при i = r. Тогда из базиса исключают вектор Аr , т.е. переменная xr на следующей итерации выйдет из состава базисных переменных и станет свободной. Элемент симплексной таблицы аrk , находящийся на пересечении направляющих столбца и строки, называется разрешающим.
. Результаты заносим в столбец Θ симплексной таблицы. Строка симплексной таблицы, соответствующая минимальному значению Θ, является направляющей. Пусть этот минимум достигается при i = r. Тогда из базиса исключают вектор Аr , т.е. переменная xr на следующей итерации выйдет из состава базисных переменных и станет свободной. Элемент симплексной таблицы аrk , находящийся на пересечении направляющих столбца и строки, называется разрешающим.
4.Определение нового опорного плана.
Для перехода к новому опорному плану производится пересчет симплексной таблицы методом Жордана- Гаусса. Сначала заменим переменные в базисе, т.е. вместо xr в базис войдет переменная аk , соответствующая направляющему столбцу.
Разделим все элементы направляющей строки r предыдущей симплексной таблицы на разрешающий элемент аrk и результаты деления занесем в строку r следующей симплексной таблицы, которая соответствует введенной в базис переменной xk. В результате этого на месте разрешающего элемента новой симплексной таблицы будем иметь «1», а в остальных клетках столбца «к» накапливаем нули. Это равносильно исключению переменной xk из всех строк таблицы (уравнений), кроме строки r, соответствующей переменной . xk .
Преобразование остальных строк симплексной таблицы, включая индексную, рассмотрим на примере строки і. Для получения новых элементов і-ой строки коэффициент а іk , находящийся на пересечении і-ой строки и k-го столбца и взятый с противоположным знаком, умножаем на элементы преобразованной направляющей строки r и складываем с соответствующими элементами і-ой строки. Результаты заносим в і-ую строку новой симплексной таблицы. Если коэффициент а іk = 0, то і-ая строка переносится в следующую симплексную таблицу без изменений.
Полученный новый опорный план снова проверяем на оптимальность. Таким образом, переходим ко второму этапу алгоритма и продолжаем процесс до получения оптимального плана.
Замечания.
1. При решении задачи линейного программирования на минимум целевой функции признаком оптимальности плана являются отрицательные значения всех коэффициентов индексной строки симплексной таблицы. Если опорный план не оптимален, то максимальное положительное значение коэффициента индексной стоки определяет выбор направляющего столбца.
2. Если в направляющем столбце все коэффициенты а іk ≤ 0, то функция цели L( 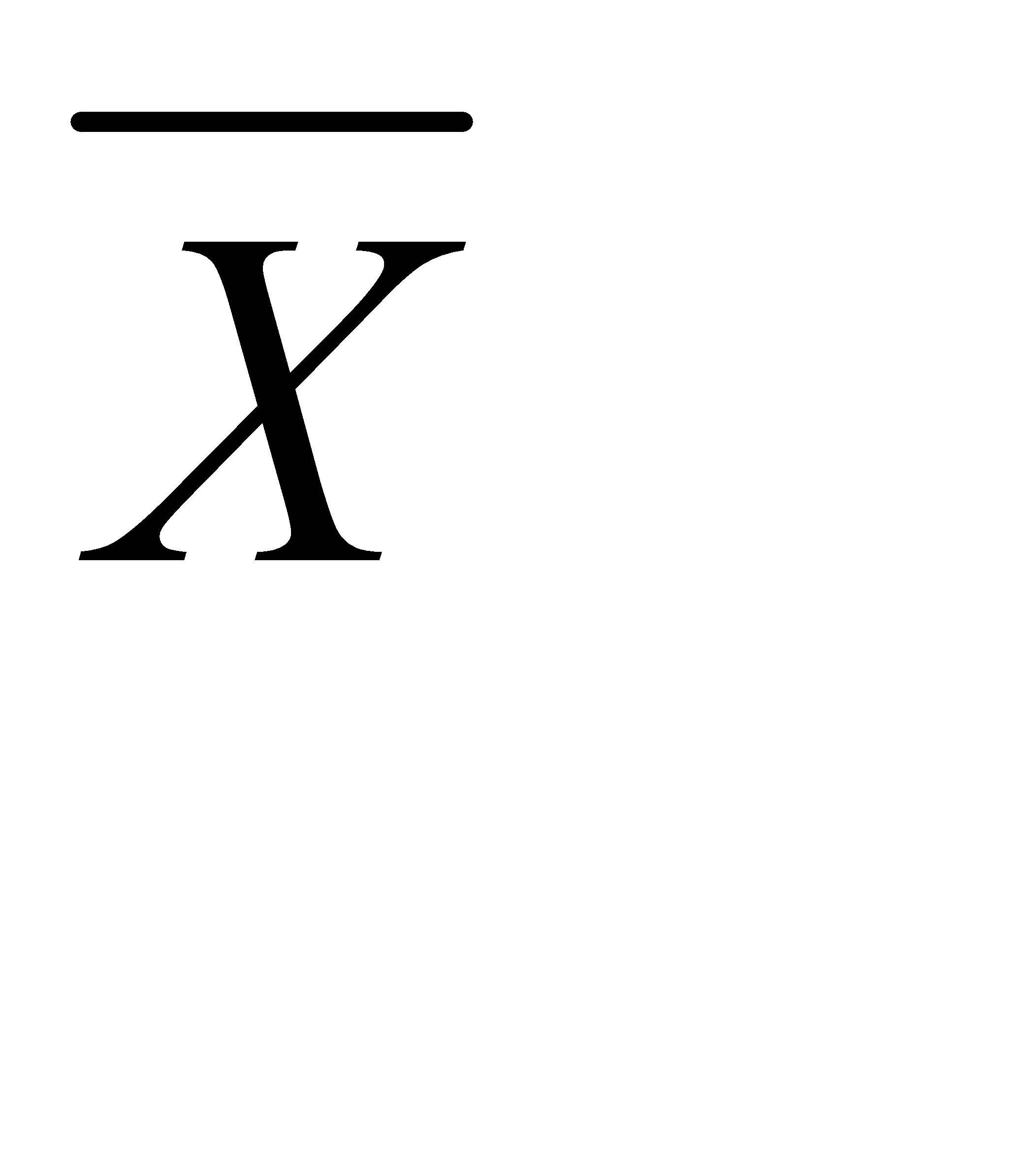 ) не ограничена на множестве допустимых планов, т.е. L(
) не ограничена на множестве допустимых планов, т.е. L( 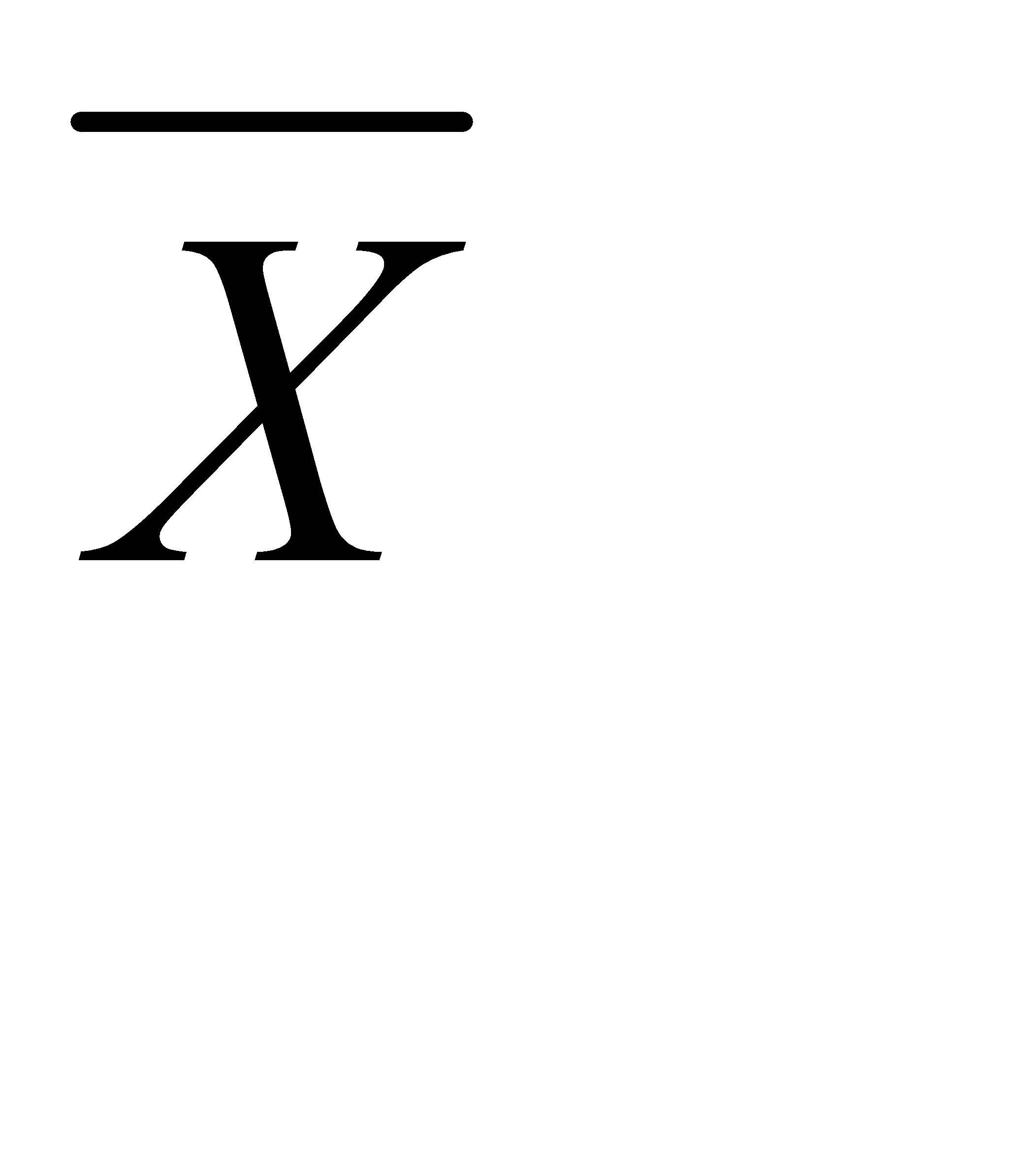 ) → ∞ и задача не имеет решения.
) → ∞ и задача не имеет решения.
3. Если в столбце θ симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным, т.е. одна или несколько базисных переменных станут равными нулю.
4. Если в оптимальный план вошла дополнительная переменная xn+1 , то это свидетельствует о недоиспользовании ресурса і-го вида в количестве значения этой переменной.
5. Если в индексной строке оптимальной симплексной таблицы находится нуль, принадлежащий столбцу свободной переменной, не вошедшей в базис, а среди коэффициентов данного столбца имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно ввести в базис, выполнив 3 и 4 этапы алгоритма, в результате будет получен второй оптимальный план с другим набором базисных переменных, но с тем же значением функции цели. Согласно основной теореме линейного программирования, любая выпуклая комбинация этих планов также является оптимальным планом задачи.
Пример.
Торговое предприятие при продаже трех групп товаров использует три вида ограниченных материально-денежных ресурсов. Нормы затрат ресурсов на реализацию единицы товарооборота (тыс.руб.), объем ресурсов и доход от реализации единицы товарооборота приведены в технологической таблице.
Определить оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль (числа условные).
| № п\п | Виды материально-денежных ресурсов (i = 1,3) | Единица измерения | Норма затрат ресурсов на реализацию 1 ед.товарооборота | Объем материально-денежных ресурсов (b і) | ||
| 1 группа (а і1) | 2 группа (а і2) | 3 группа (а і3) | ||||
| 1. 2. 3. | Рабочее время продавцов Площадь торговых залов Площадь складских помещений | Чел.-час. м2 м2 | ||||
| Прибыль от реализации ед. т/о | Тыс.руб. | max |
Запишем математическую модель задачи.
Определить 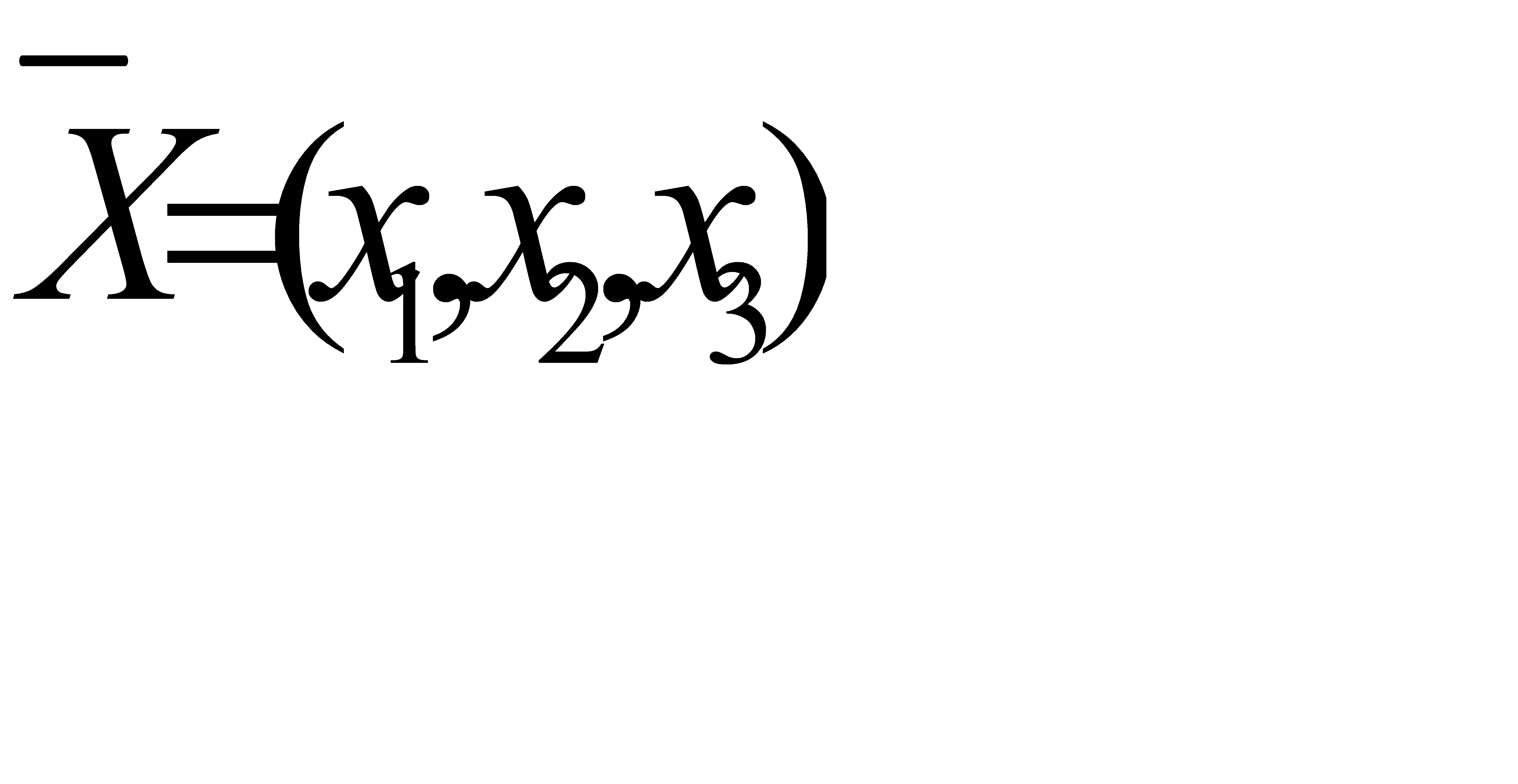 , который удовлетворяет условиям
, который удовлетворяет условиям
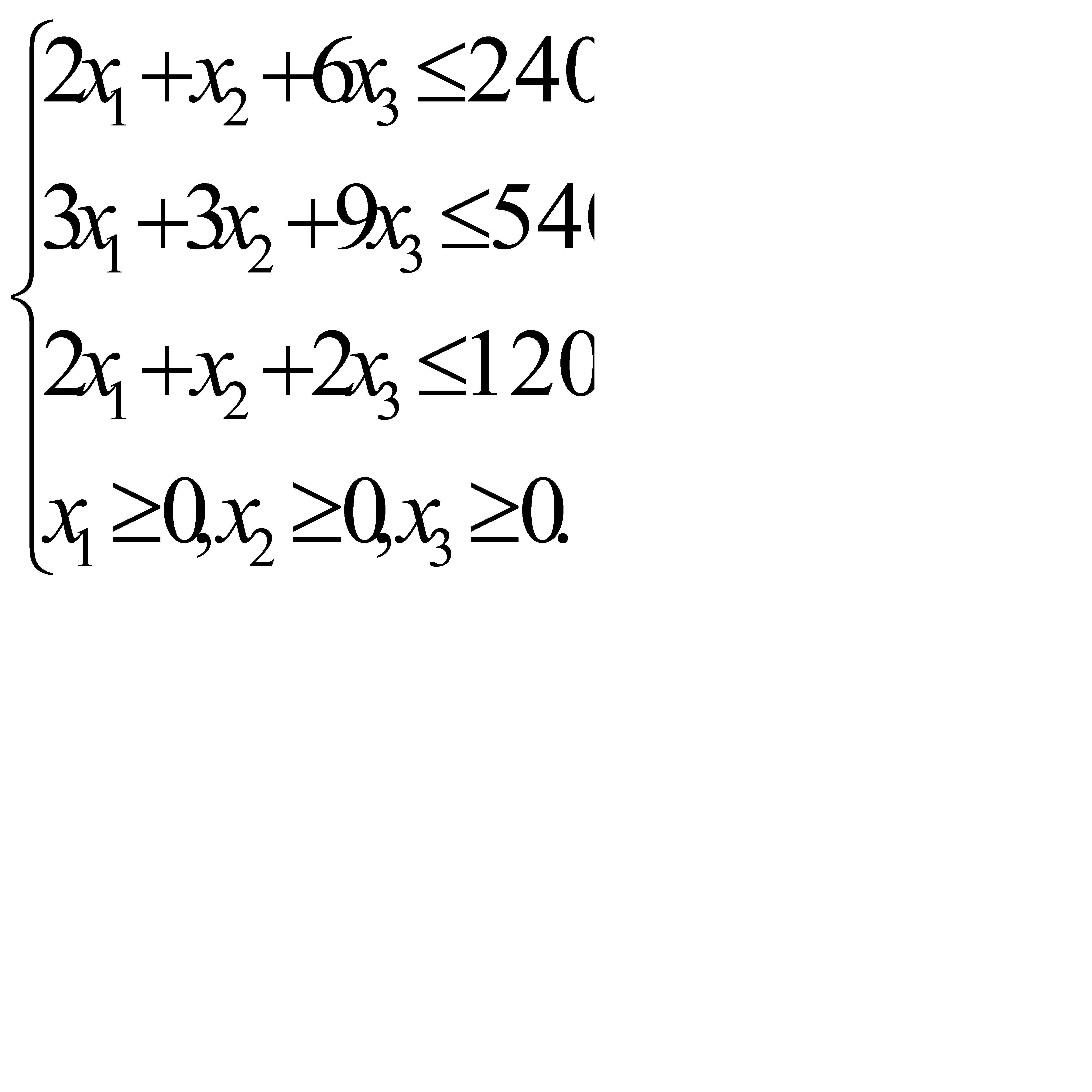

и доставляет максимальное значение целевой функции
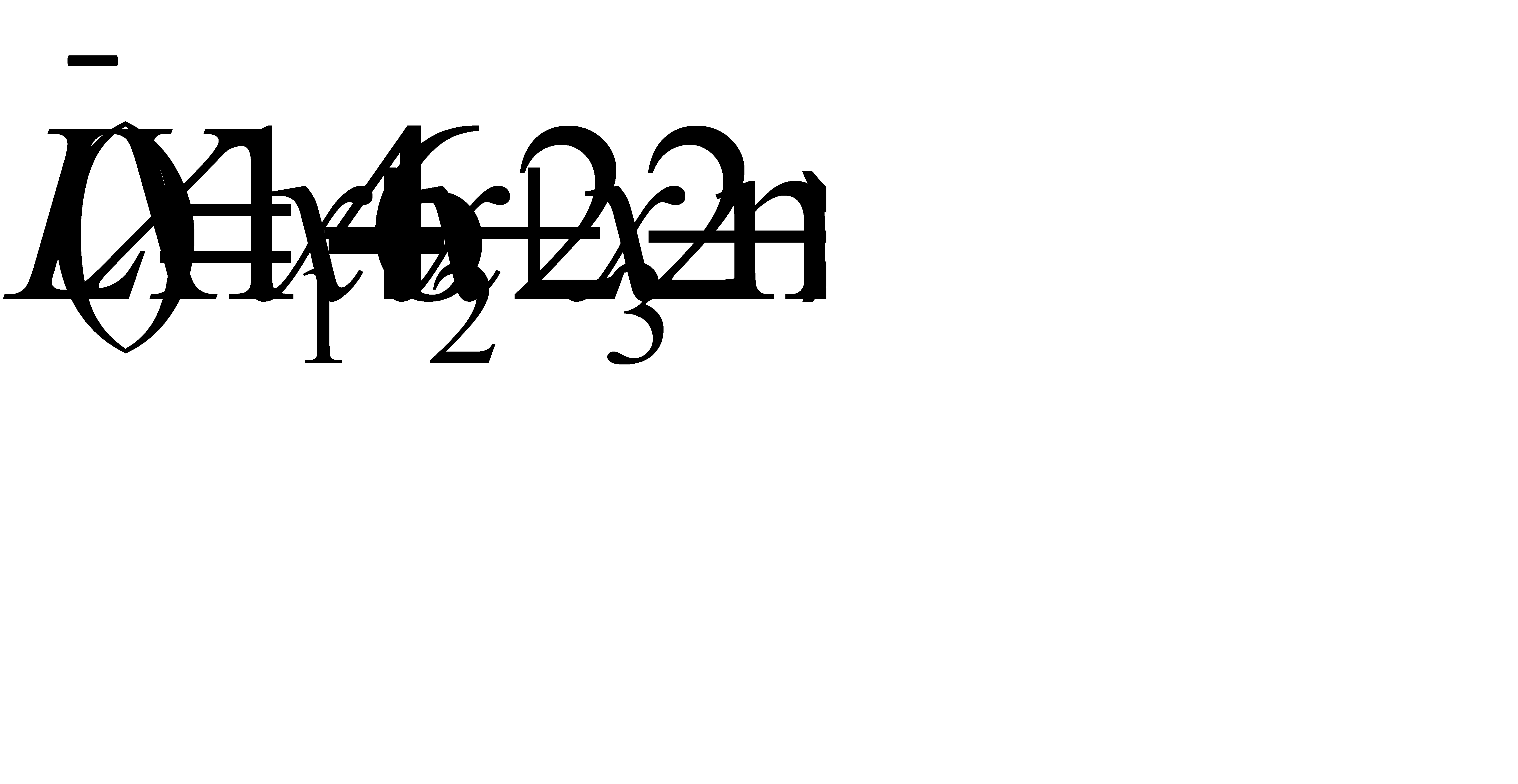 . (2.9)
. (2.9)
Задачу (2.8) – (2.9) решим симплексным методом.
Для получения первого опорного плана систему неравенств (2.7) приведем к системе уравнений
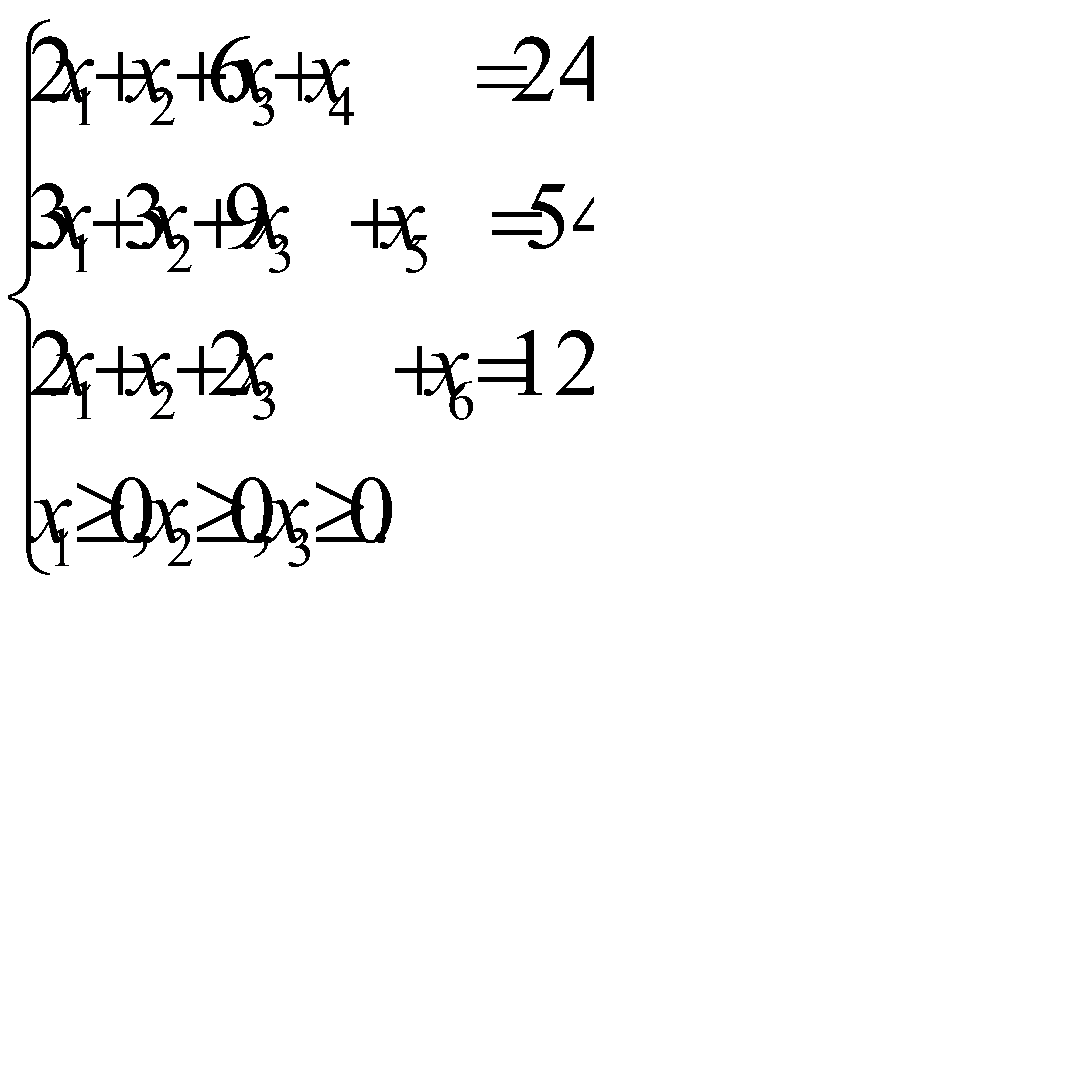 (2.10)
(2.10)
В системе уравнений 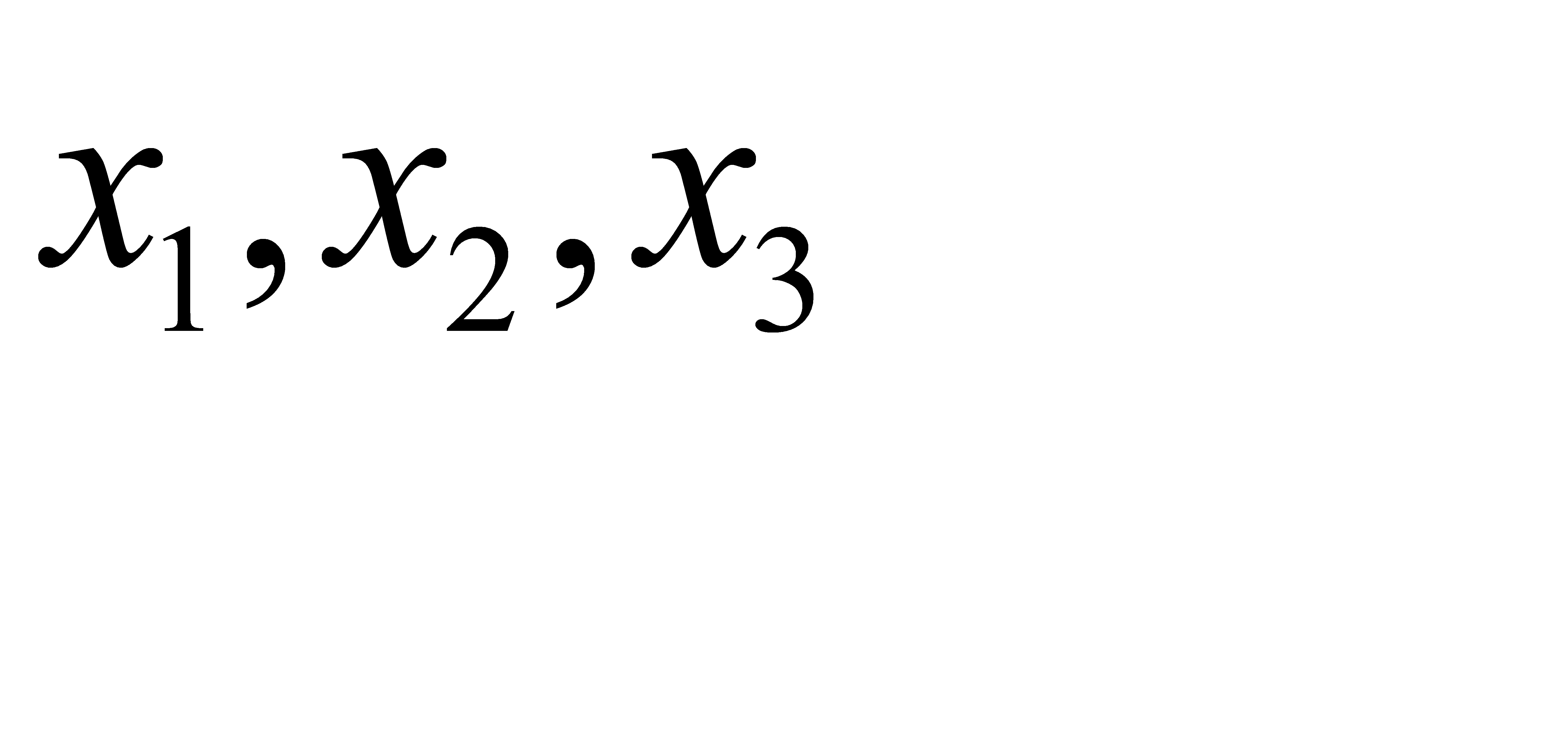 - основные переменные, характеризующие объемы реализации 1, 2 и 3 групп товаров соответственно,
- основные переменные, характеризующие объемы реализации 1, 2 и 3 групп товаров соответственно, 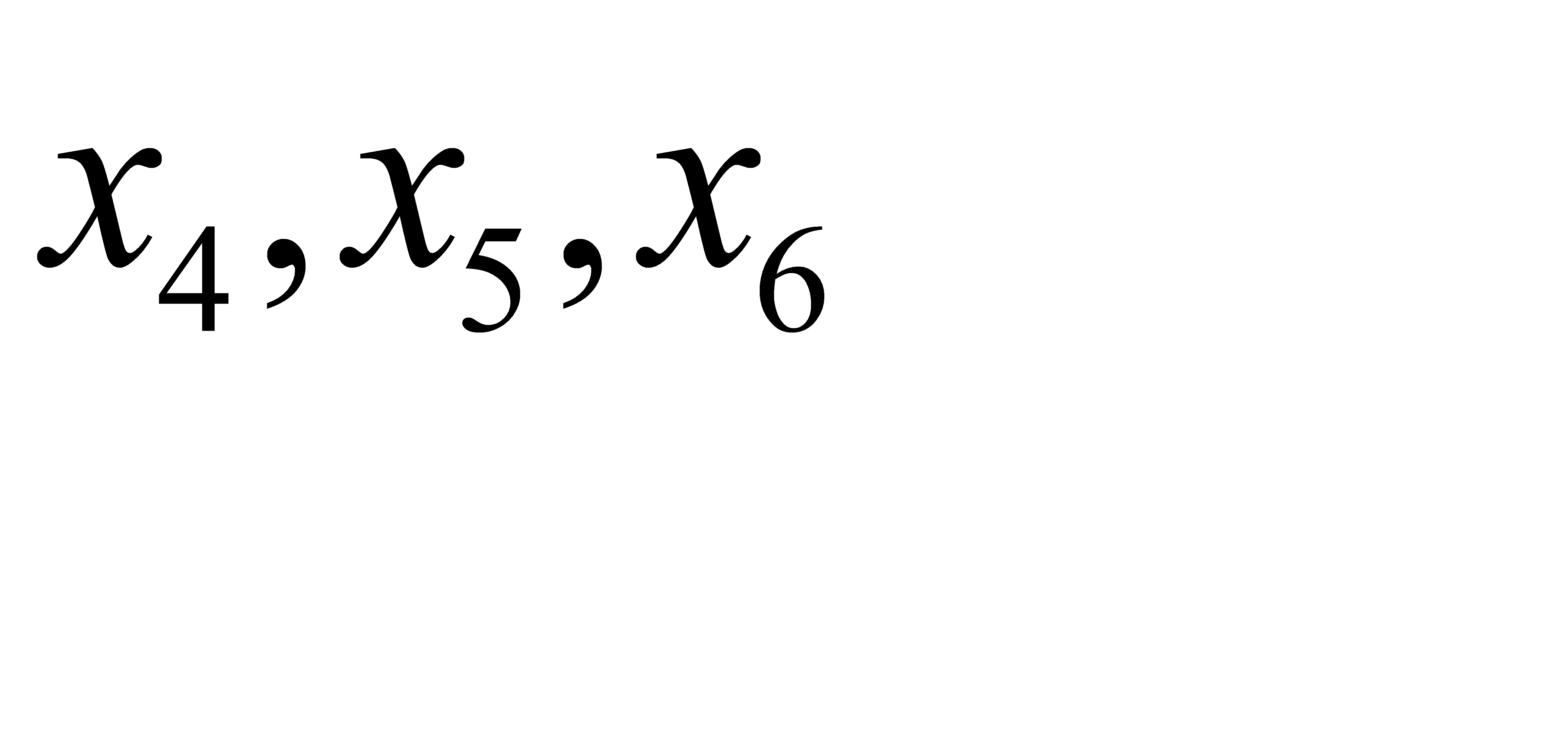 - дополнительные переменные, определяющие объемы ресурсов.
- дополнительные переменные, определяющие объемы ресурсов.
Решим систему уравнений (2.10) относительно базисных переменных
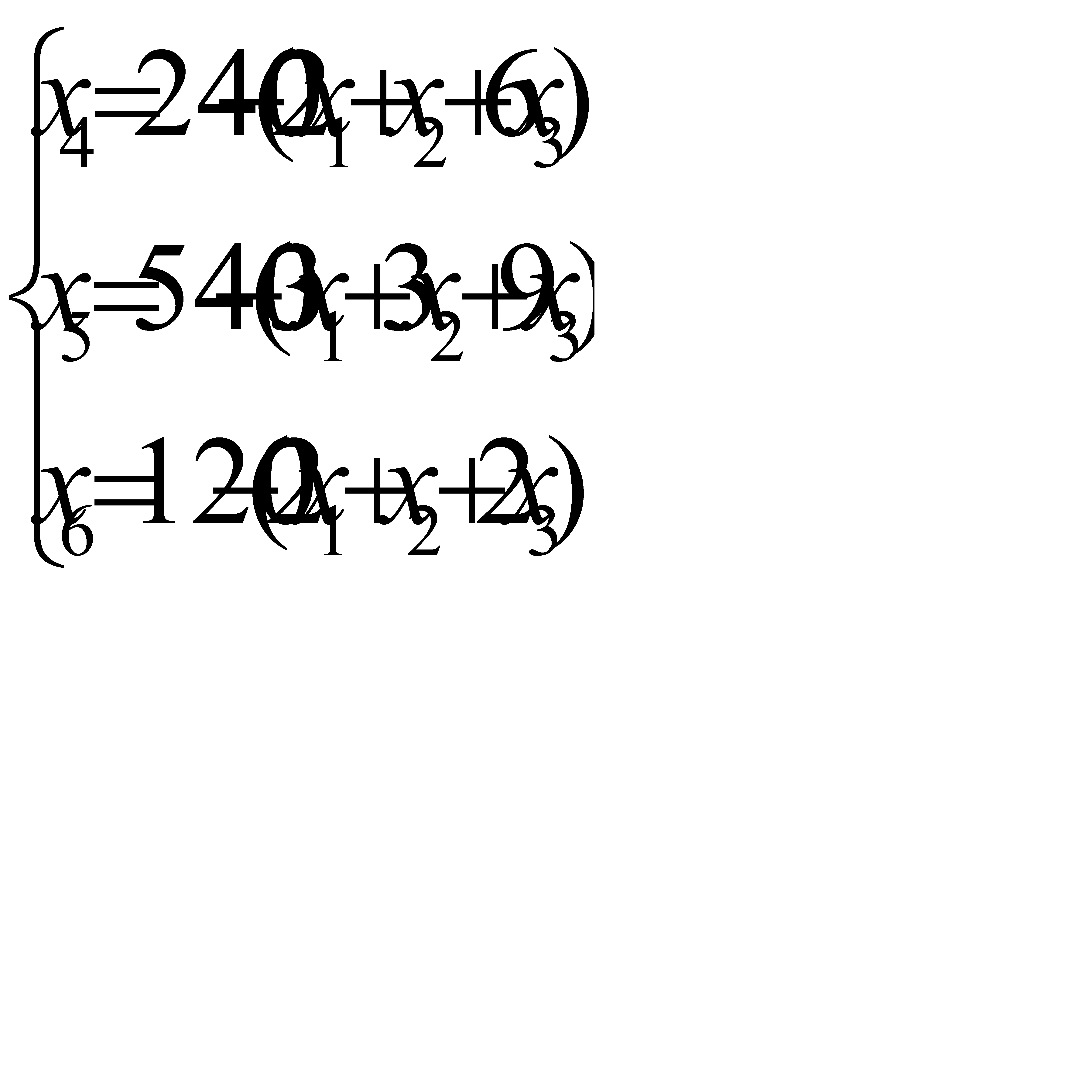
Функцию цели запишем в виде: 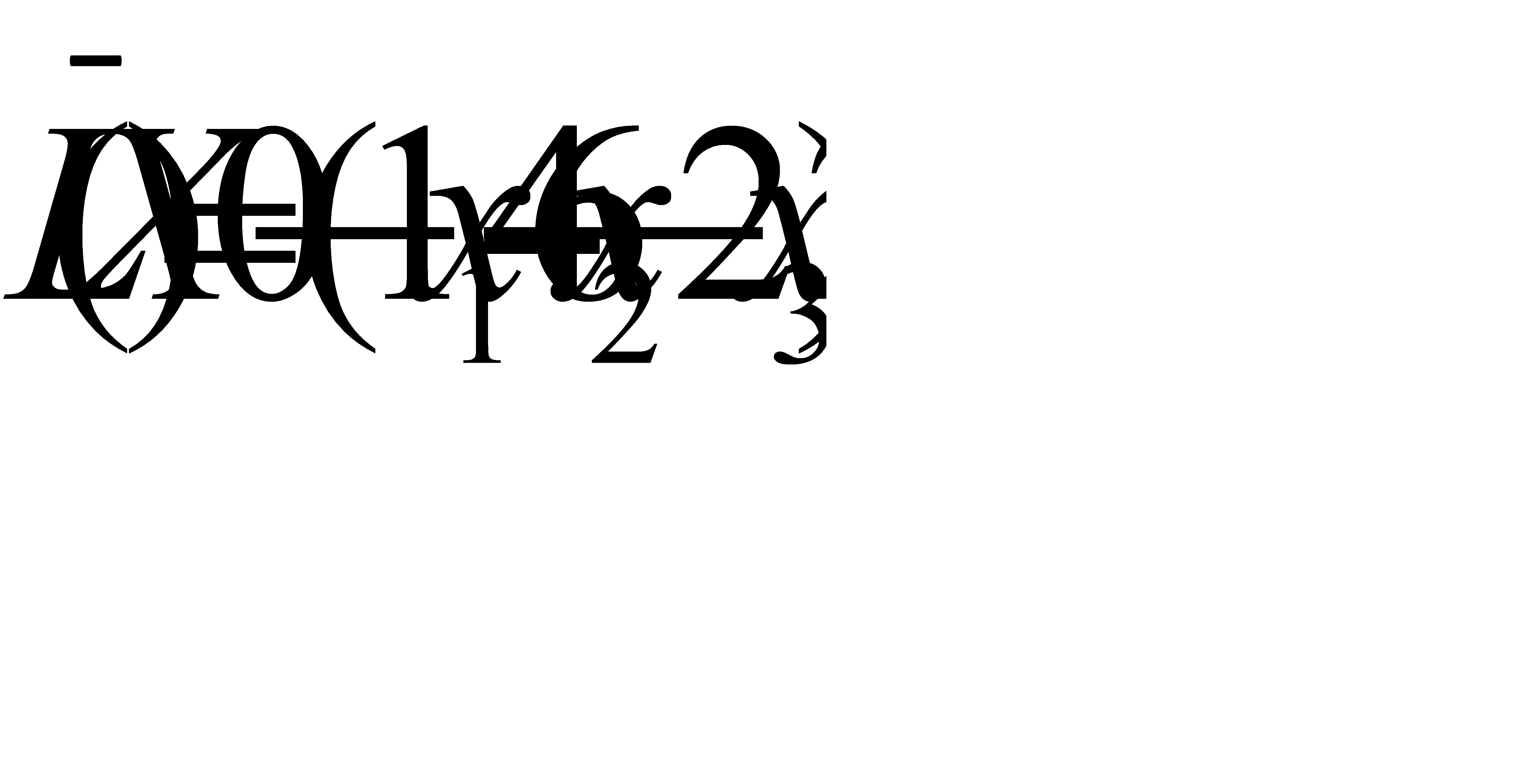 (2.12)
(2.12)
Полагая, что свободные переменные 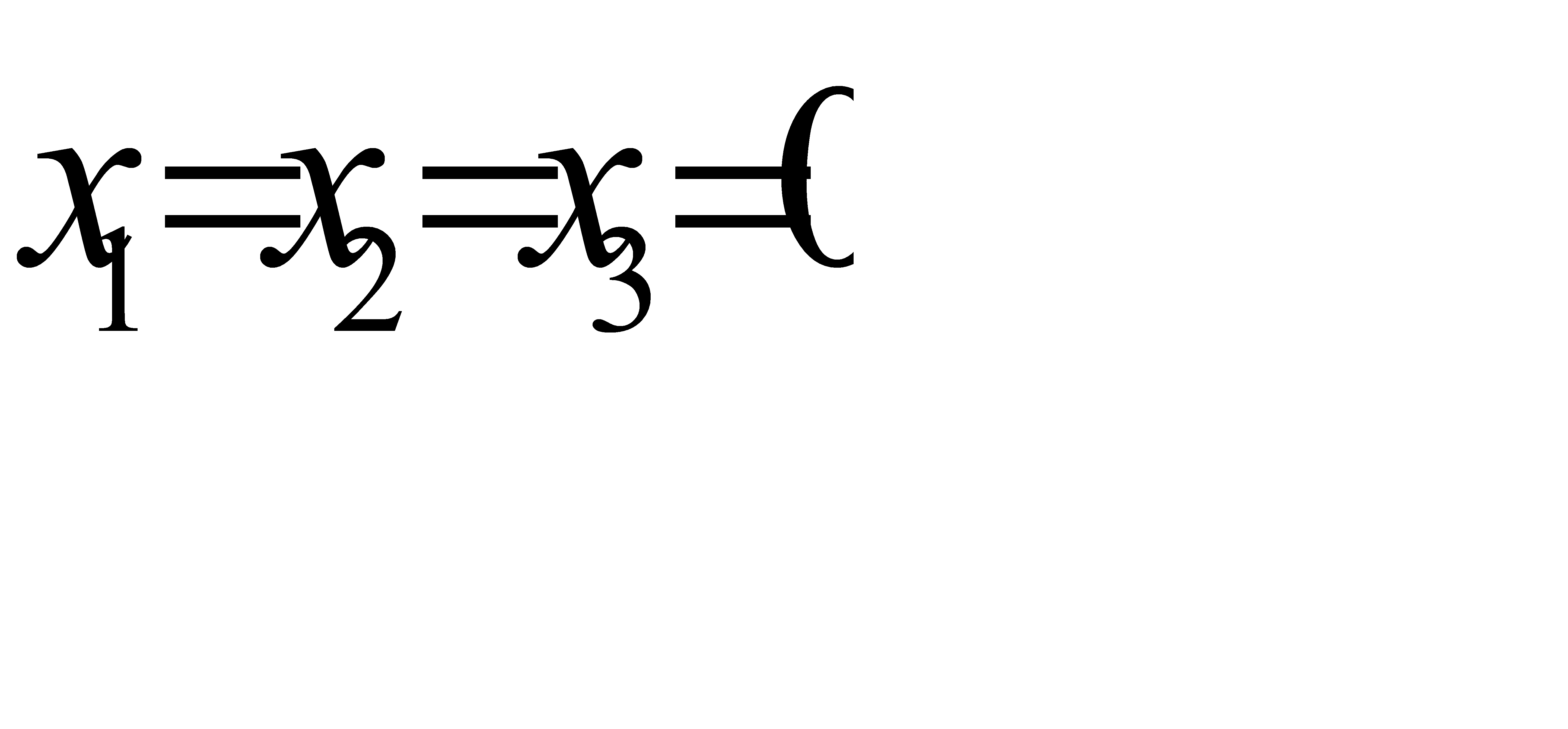 , получим первый опорный план:
, получим первый опорный план:  ,
, 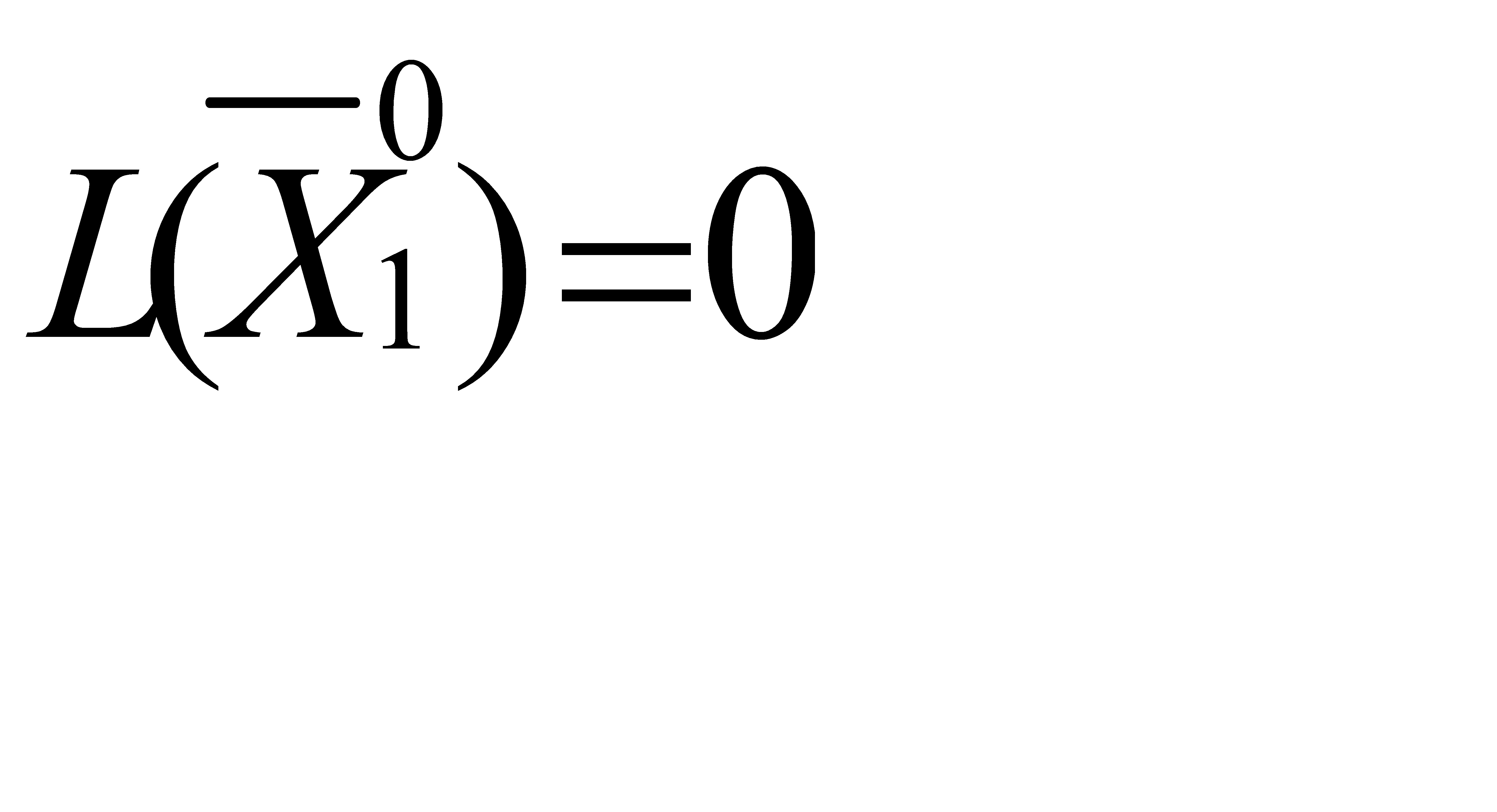 , в котором базисные переменные
, в котором базисные переменные 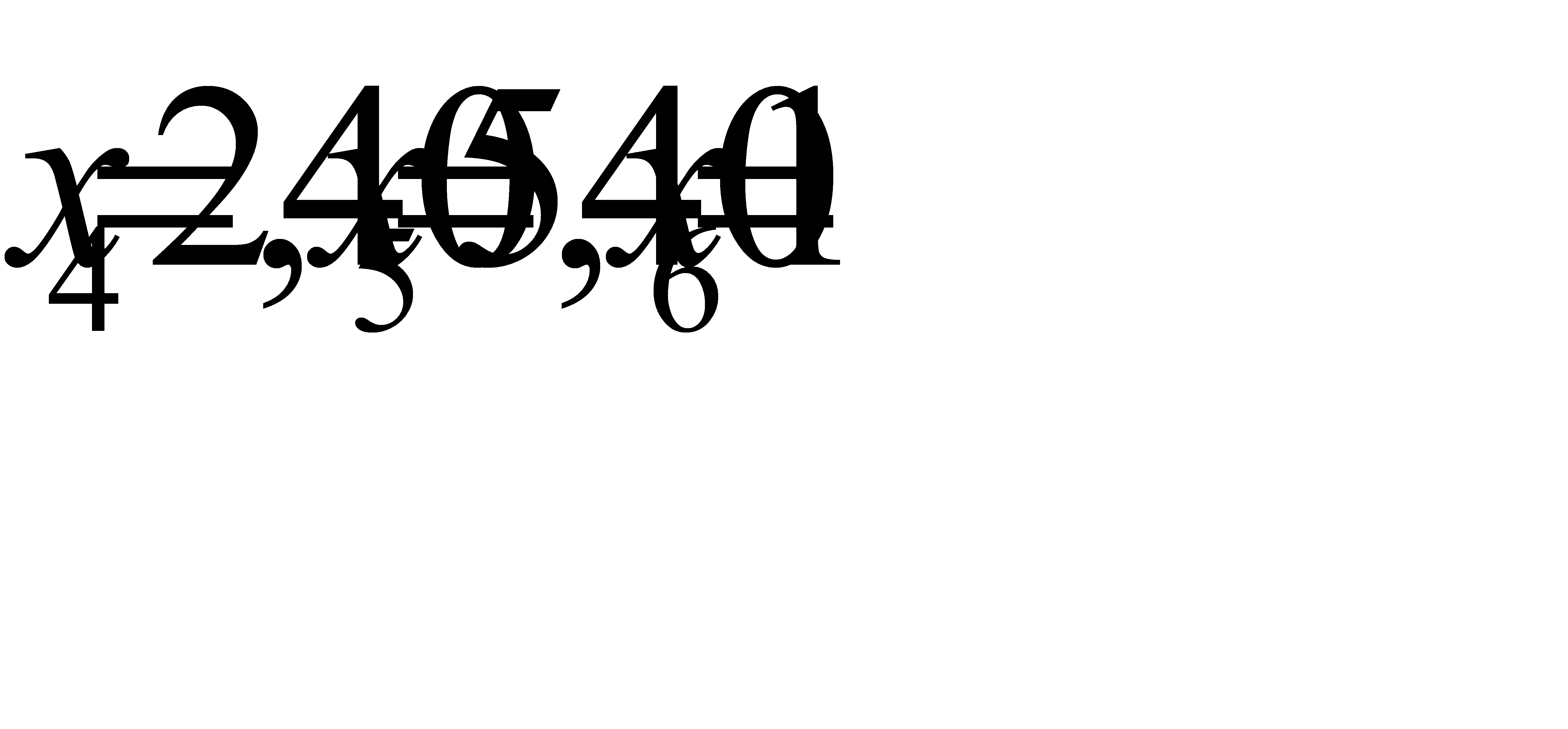 .
.
Первый опорный план заносим в симплексную таблицу (см. таблицу0. этот план является не оптимальным, так как в индексной строке находятся отрицательные коэффициенты: –14, –6, –22. Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине. Так как |–22| > {|–14|, |–6|}, то направляющий столбец соответствует переменной x3. Тогда на следующей итерации переменная x3 перейдет из свободных в базисные. Элементы столбца свободных членов симплексной таблицы разделим на соответствующие положительные коэффициенты направляющего столбца: 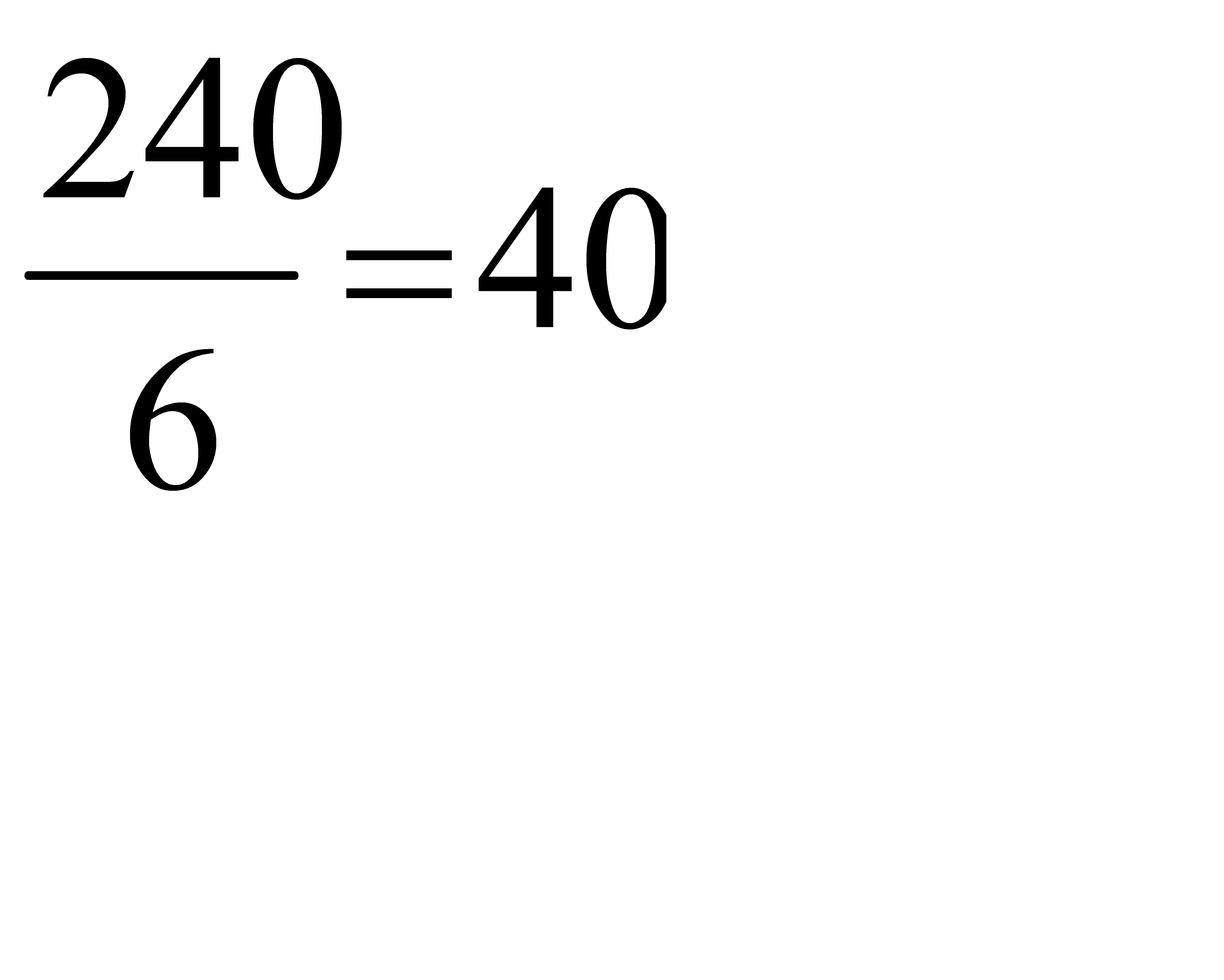 ;
; 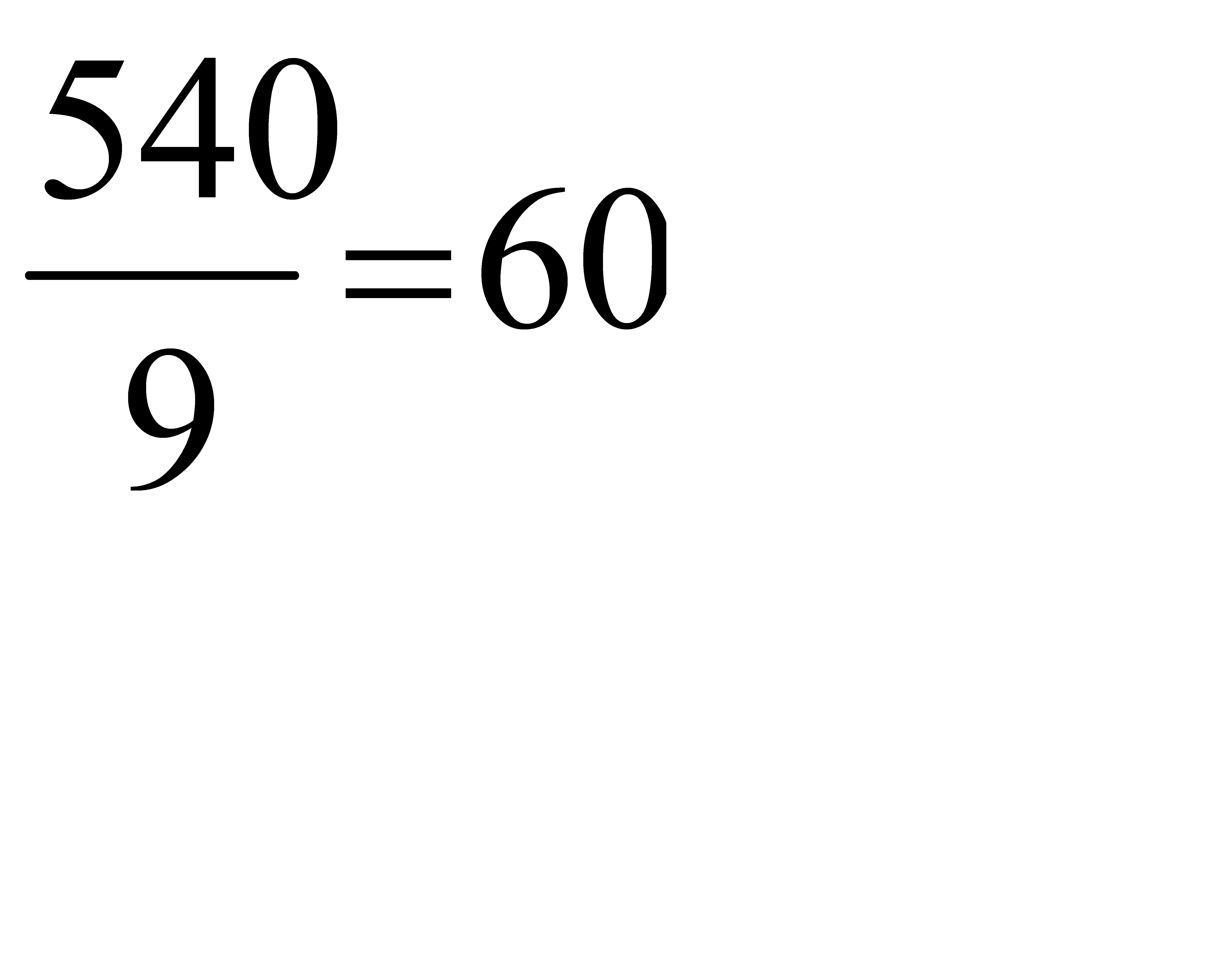 ;
; 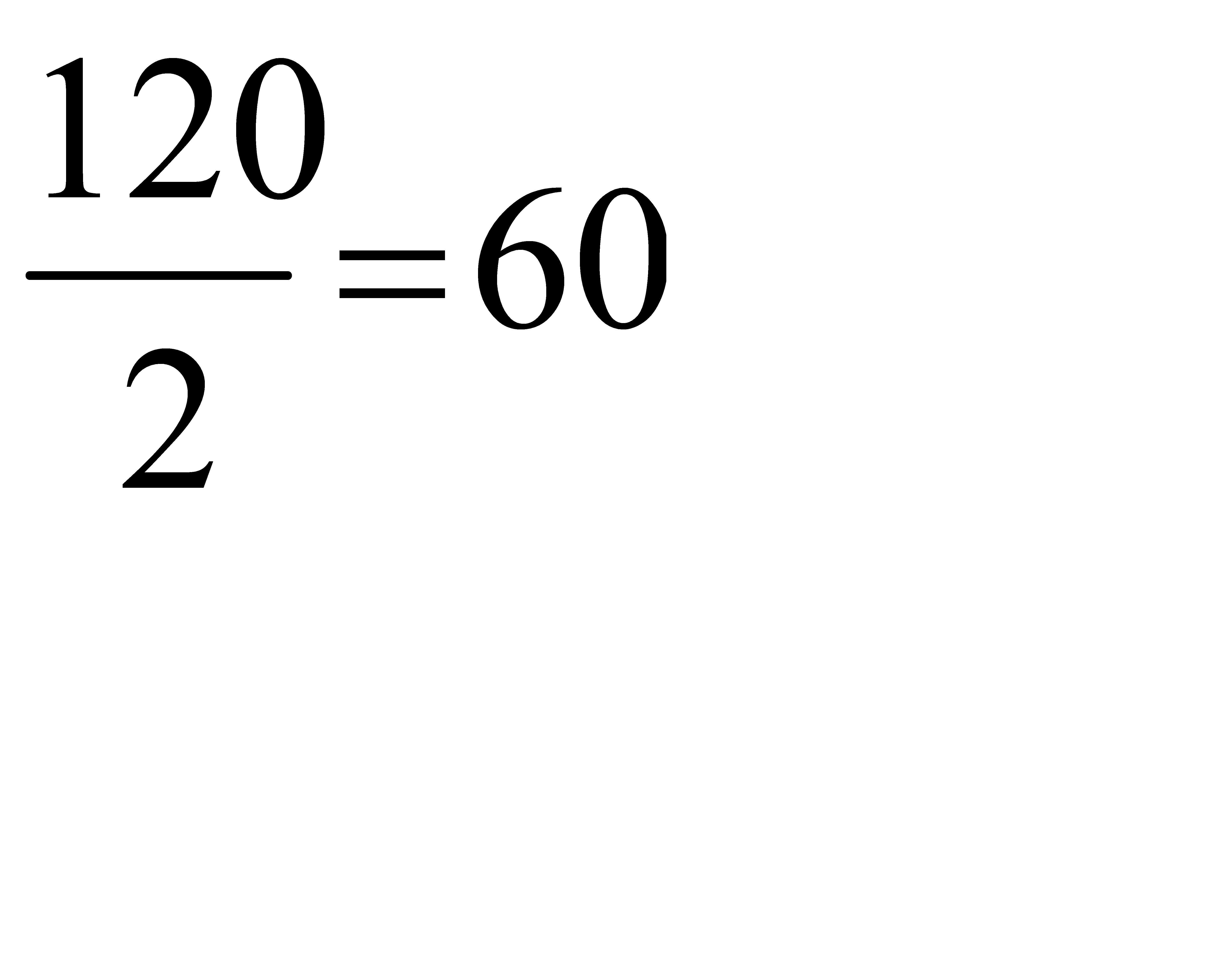 . Из трех значений столбца θ выбираем min{40,60,60}= 40. Строка симплексной таблицы, соответствующая минимальному значению θ, является направляющей. Она определяет переменную x4, которая на следующей итерации перейдет из базиса и станет свободной. На пересечении направляющих столбца и строки находится разрешающий элемент, равный 6. В таблице 1 направляющие столбец и строка помечены стрелками, а разрешающий элемент обведен кругом.
. Из трех значений столбца θ выбираем min{40,60,60}= 40. Строка симплексной таблицы, соответствующая минимальному значению θ, является направляющей. Она определяет переменную x4, которая на следующей итерации перейдет из базиса и станет свободной. На пересечении направляющих столбца и строки находится разрешающий элемент, равный 6. В таблице 1 направляющие столбец и строка помечены стрелками, а разрешающий элемент обведен кругом.
Формируем следующую симплексную таблицу 2. Вместо переменной x4 в таблицу 2 вошла переменная x3. Строка, соответствующая переменной x3 получена в результате деления всех элементов направляющей строки (строка переменной x4 таблицы 1) на разрешающий элемент 6. На месте разрешающего элемента в таблице получаем «1». В остальных клетках столбца x3 таблицы 2 накапливаем нули методом Жордана-Гаусса.
Рассмотрим преобразование второй строки симплексной таблицы, которая соответствует переменной x4 . Для получения новых значений элементов данной строки необходимо все элементы преобразованной направляющей строки таблицы 2 умножить на число, стоящее на пересечении строки x5 и столбца x3 таблицы 1, взятое с противоположным знаком, т.е. на (–9). Результаты умножения сложить с соответствующими элементами строки x5 таблицы 1 и записать в строку x5 таблицы 2.
40·(–9) + 540 = 180
 ·(–9) + 3 = 0
·(–9) + 3 = 0
 ·(–9) + 3 =
·(–9) + 3 = 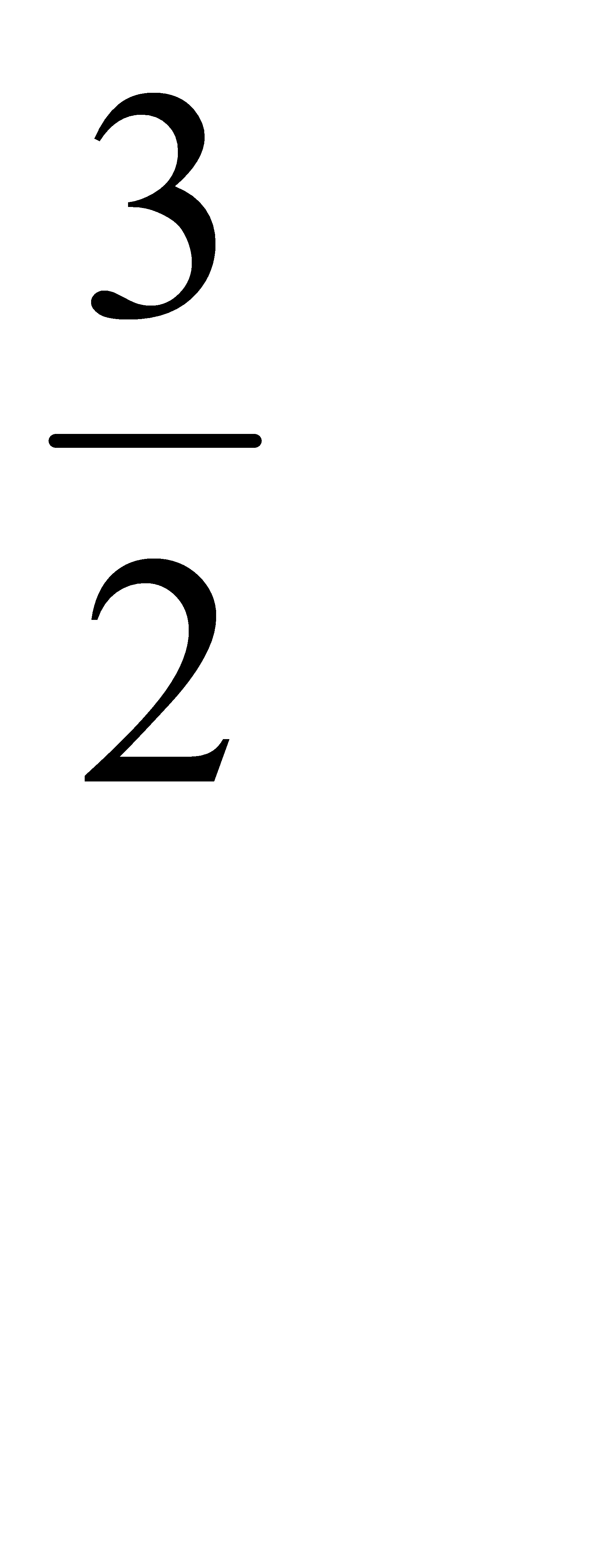
1·(–9) + 9 = 0
 ·(–9) + 0 = –
·(–9) + 0 = – 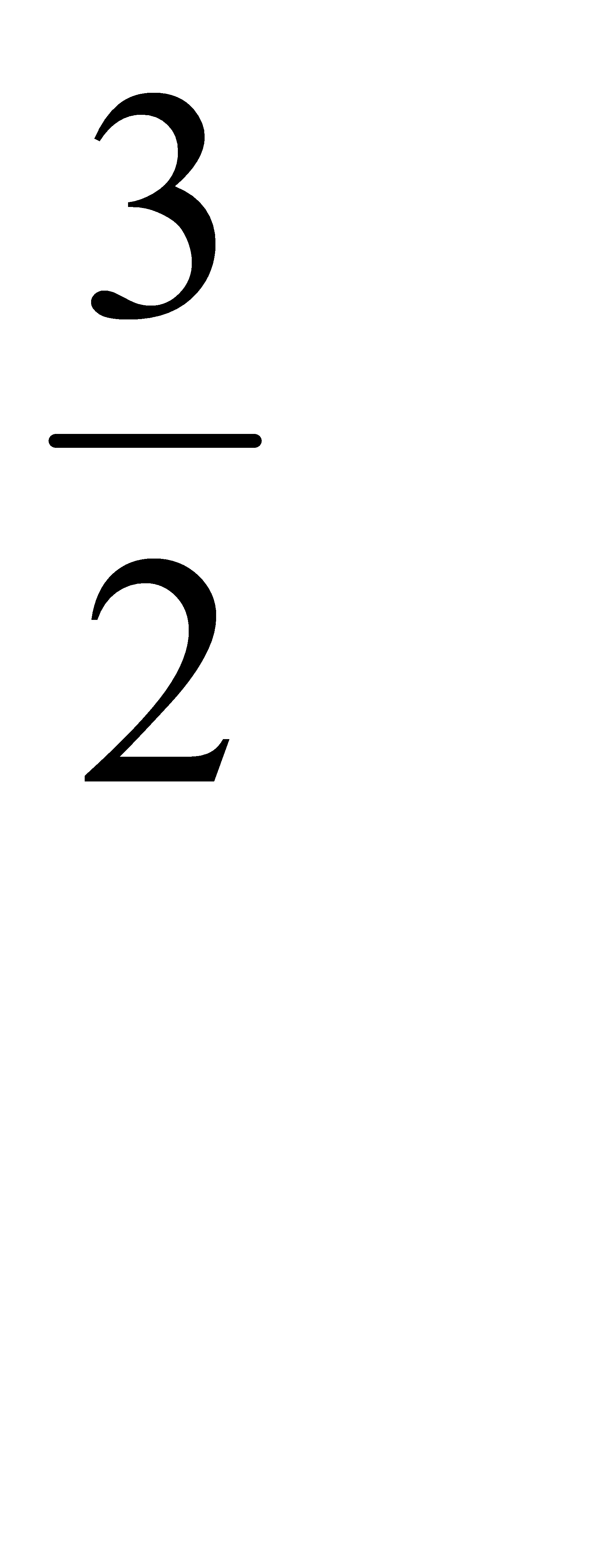
0·(–9) + 1 = 1
0·(–9) + 0 = 0.
Аналогично проводятся расчеты по всем строкам таблицы, включая индексную.
Далее возвращаемся к этапу 2 алгоритма – проверка оптимальности опорного плана. Выполняя последовательно все этапы алгоритма, заполняем таблицу 3.
На третьей итерации в таблице 3 получен оптимальный план, так как все коэффициенты в индексной строке ∆j ≥ 0, j = 1, 6.
Запишем оптимальный план:
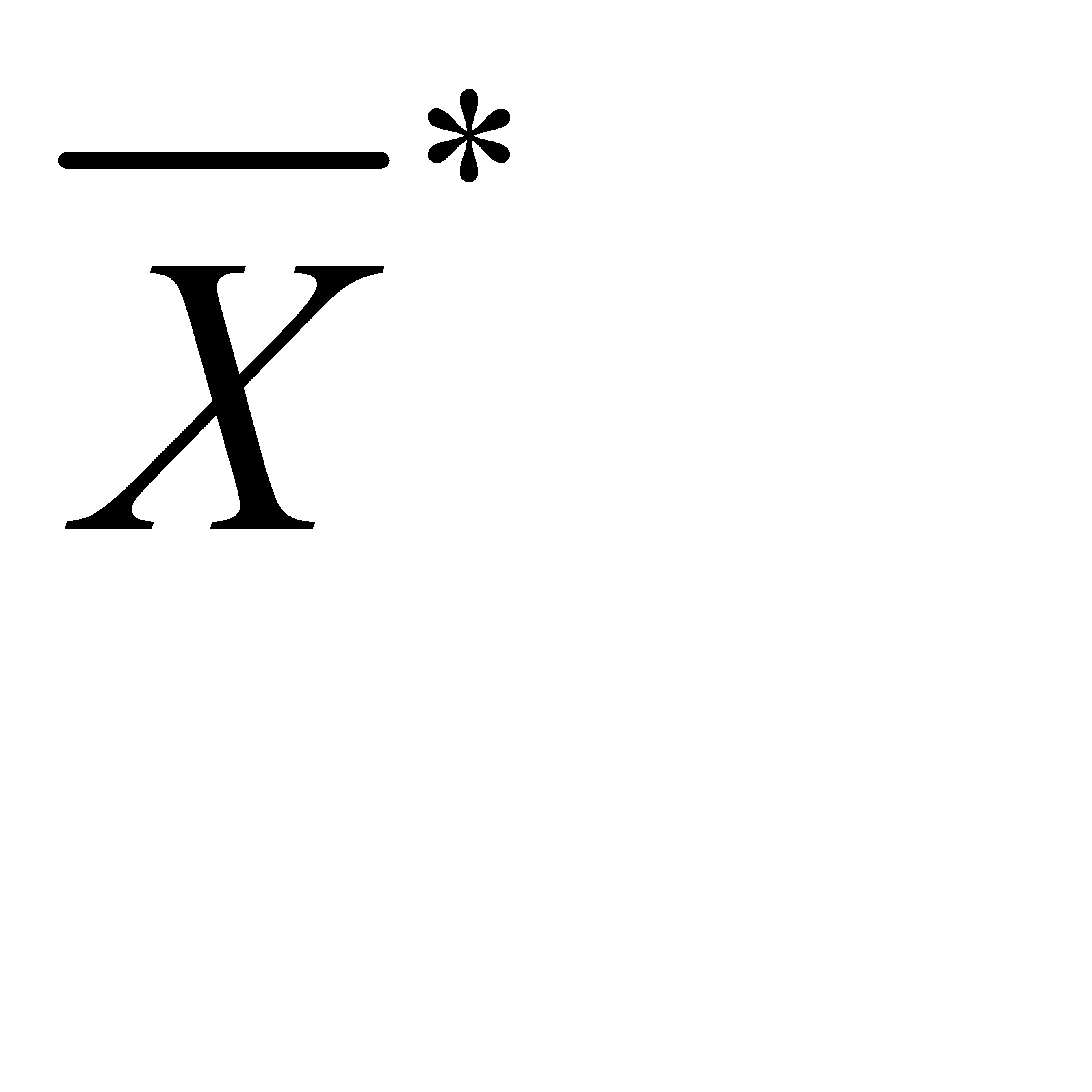 = (30, 0, 30, 0, 180, 0), L(
= (30, 0, 30, 0, 180, 0), L( 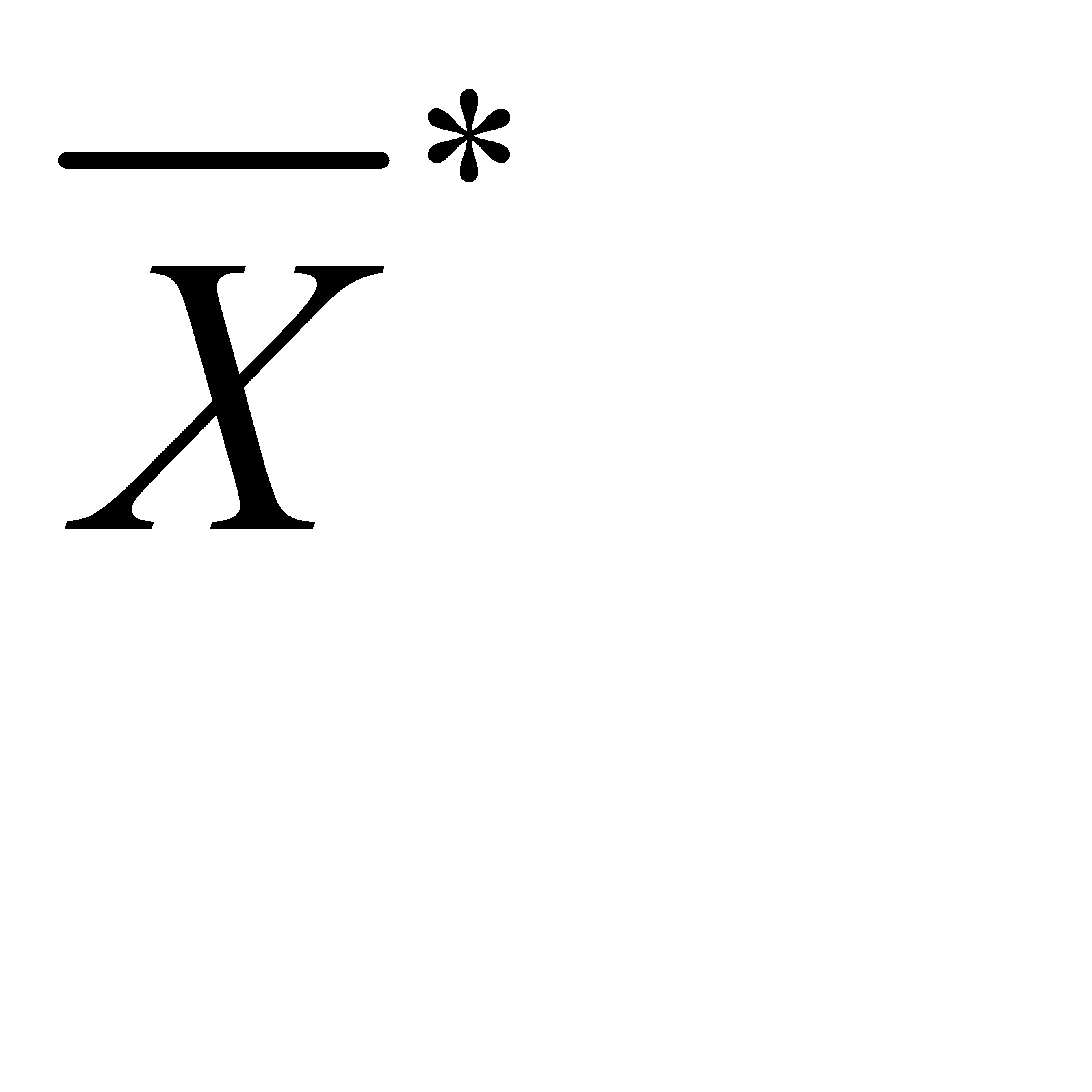 ) = 1080 (тыс.руб.).
) = 1080 (тыс.руб.).
Следовательно, для получения максимальной прибыли в размере 1080 тыс. руб. торговому предприятию необходимо продавать товаров 1-ой группы 30 ед. (х1*= 30) и товаров 3-ей группы 30 ед. (х3*= 30). В оптимальный план вошла дополнительная переменная х5*= 180. Это указывает на то, что ресурсы второго вида (площади торговых залов) недоиспользованы на 180 м2, остальные ресурсы использованы полностью, так как х4*= х6*= 0.
Полученный в результате решения оптимальный план является невырожденным, так как при расчете столбца θ не были получены одинаковые минимальные значения и все значения базисных переменных в оптимальном плане отличны от нуля.
В индексной строке таблицы 3 в строках переменных 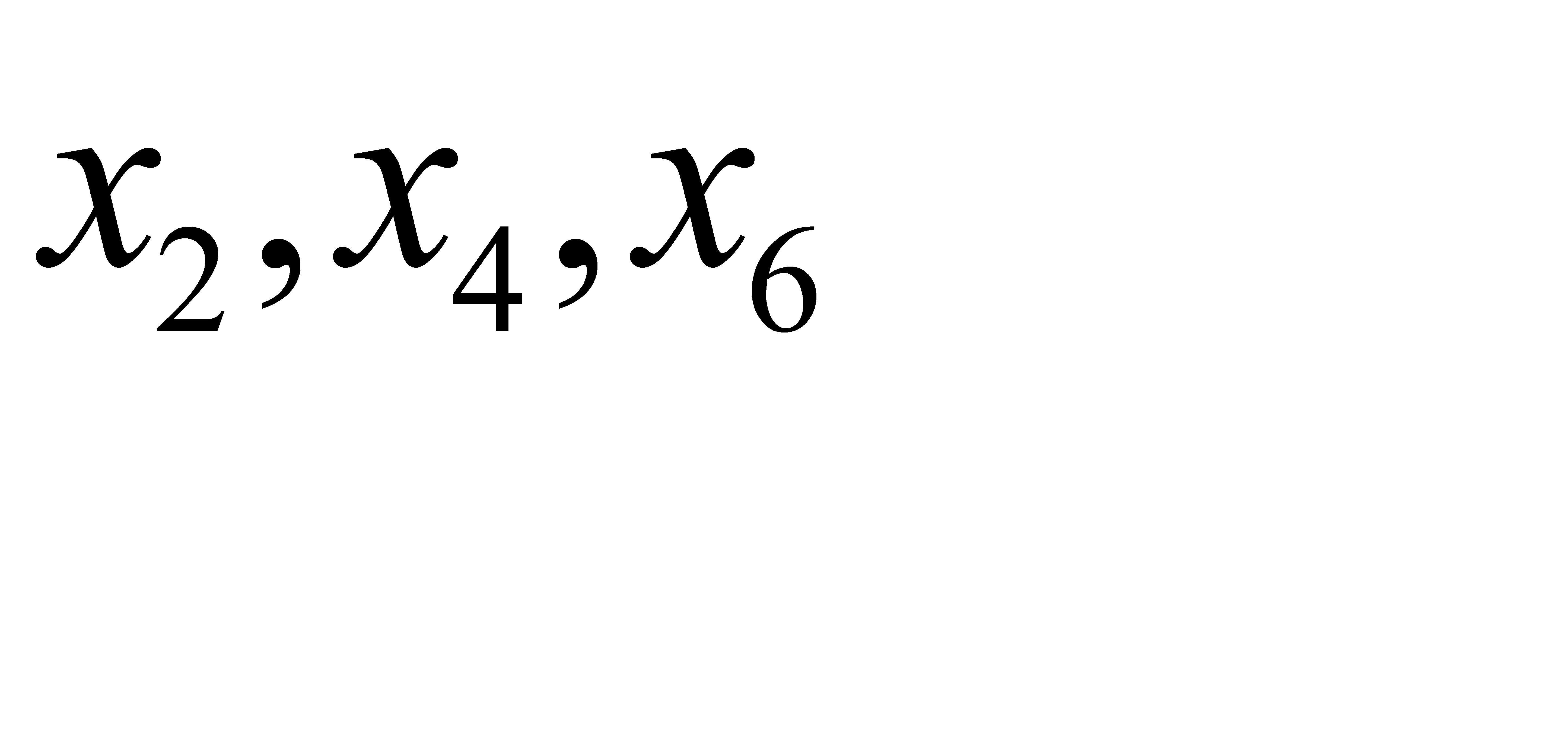 , не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи является единственным.
, не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи является единственным.
| Таблица 1 | Базисные перемен- ные | Свободные члены (значения базисных перемнных) | x1 | x2 | x3 | x4 | x5 | x6 | θ |
| ←x4 | |||||||||
| x5 | |||||||||
| x6 | |||||||||
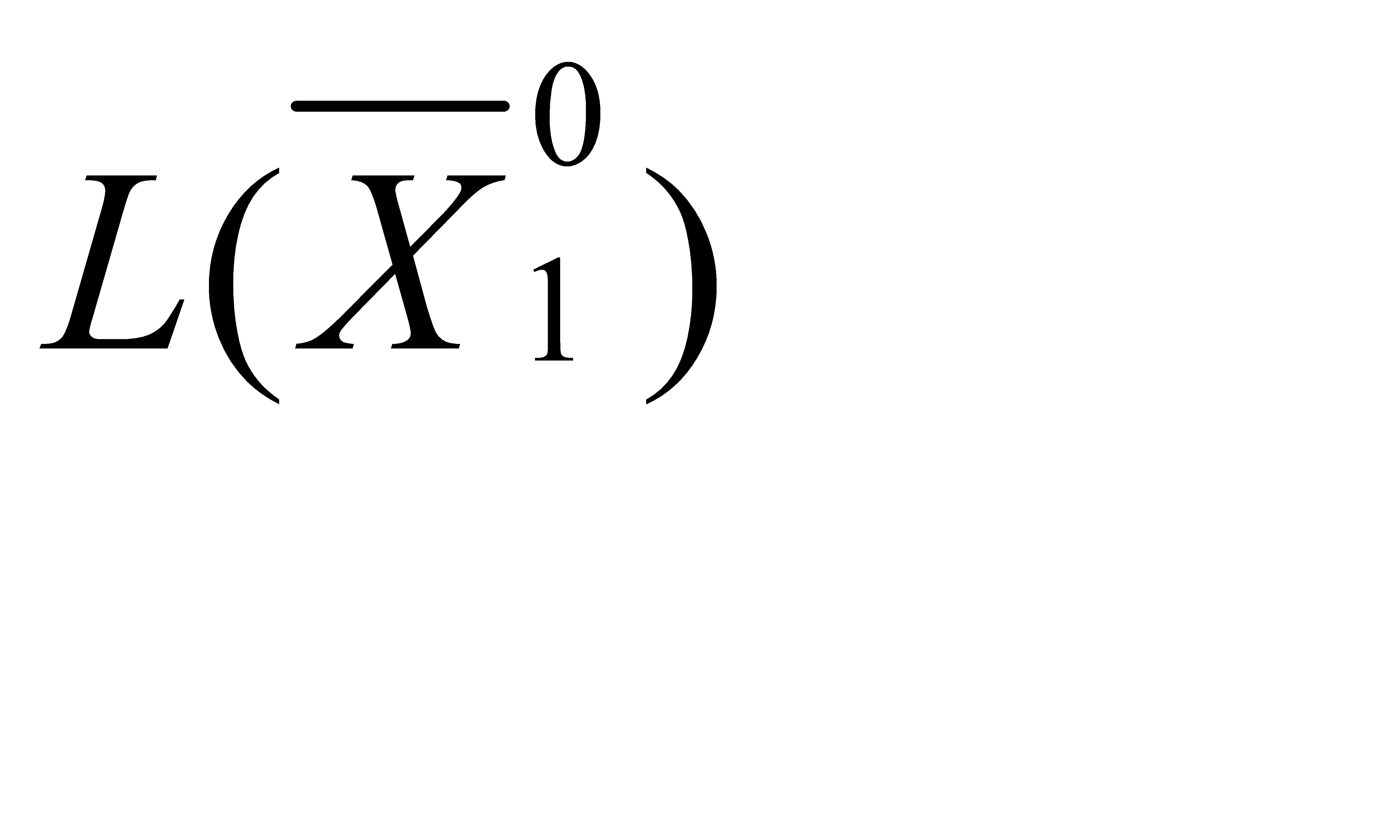
| –14 | –6 | –22↑ | ||||||
| Таблица 2 | x3 | 
| 
| 
| |||||
| x5 | 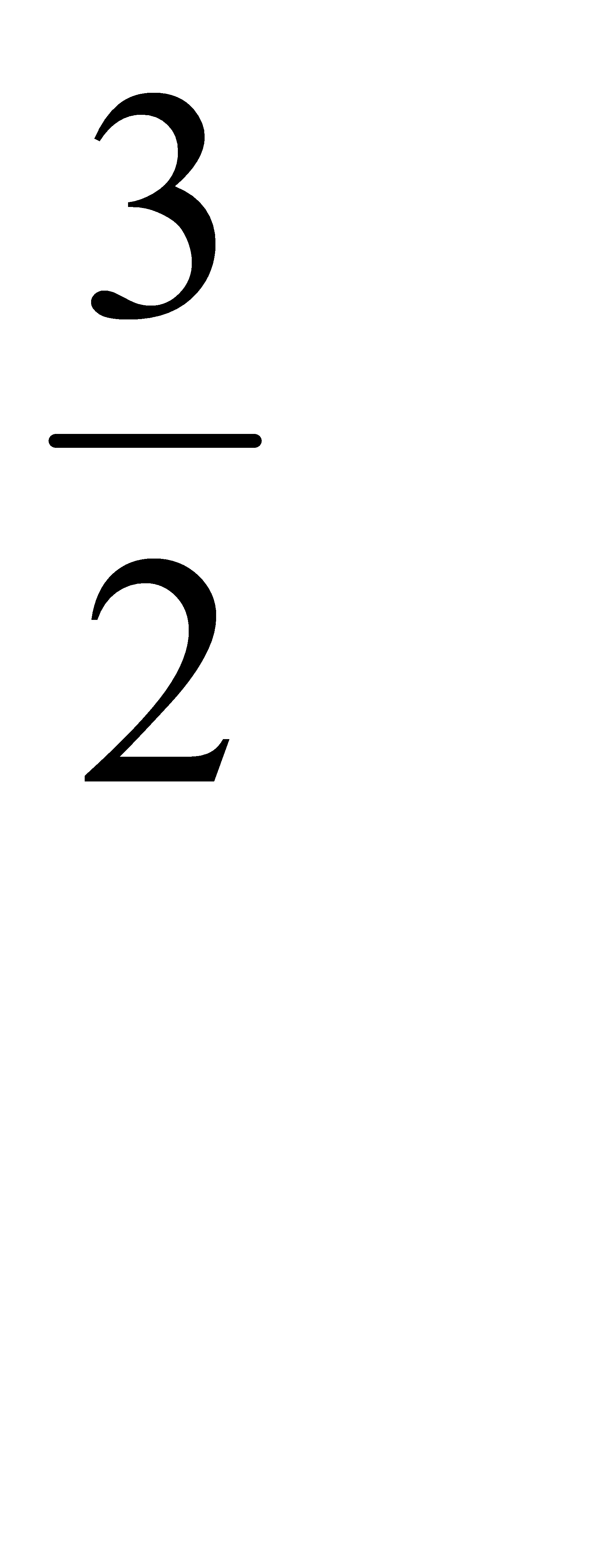
| – 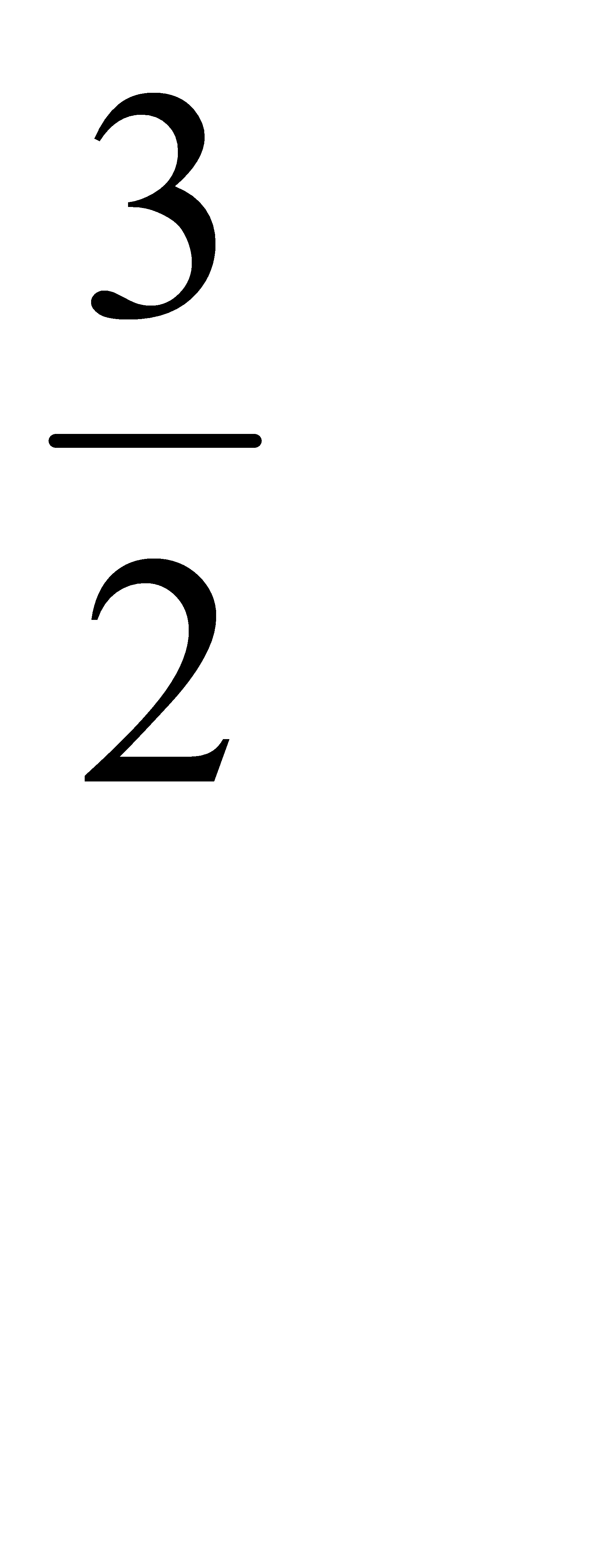
| – | ||||||
| ←x6 | 
| 
| – 
| ||||||
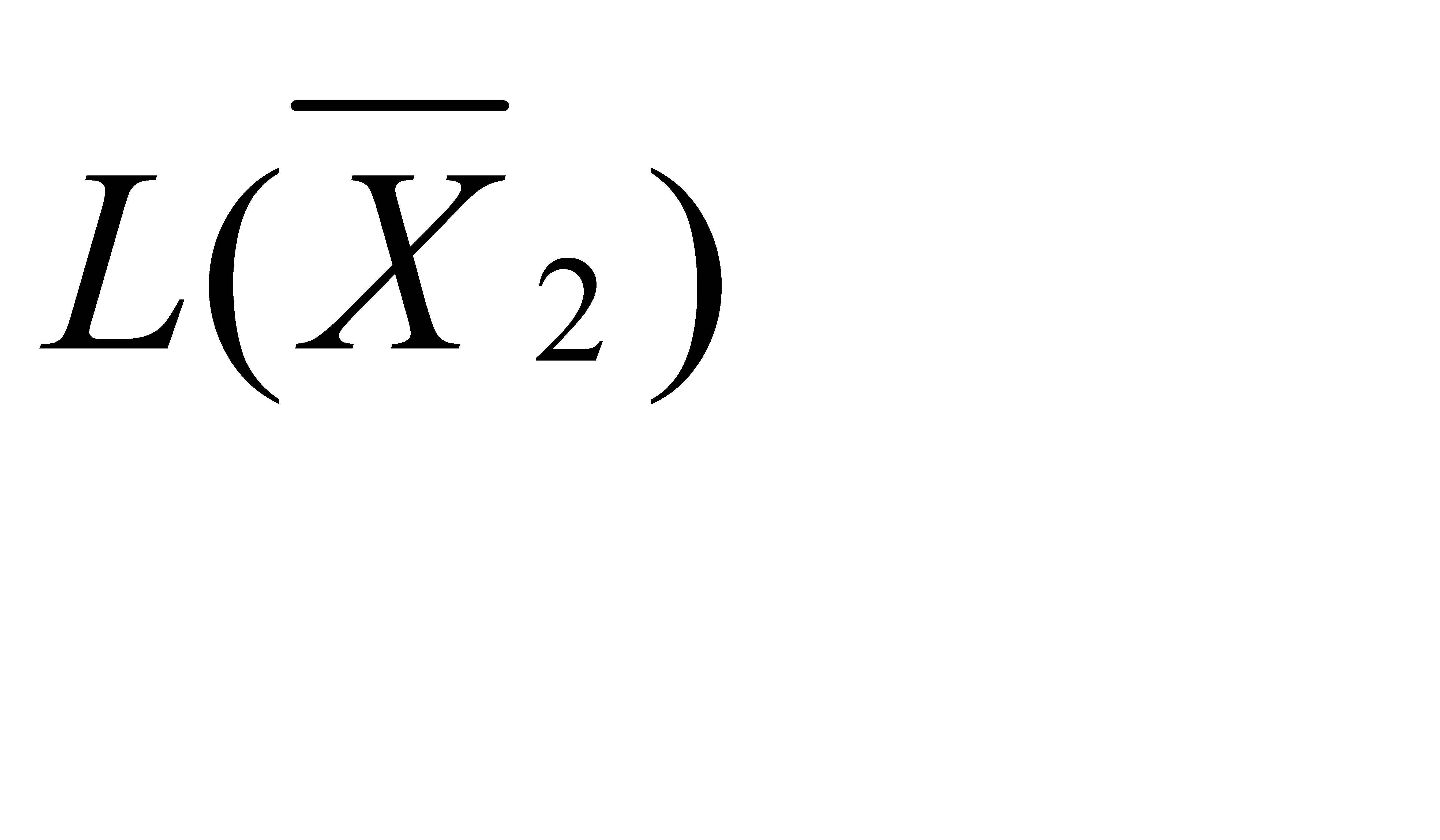
| – 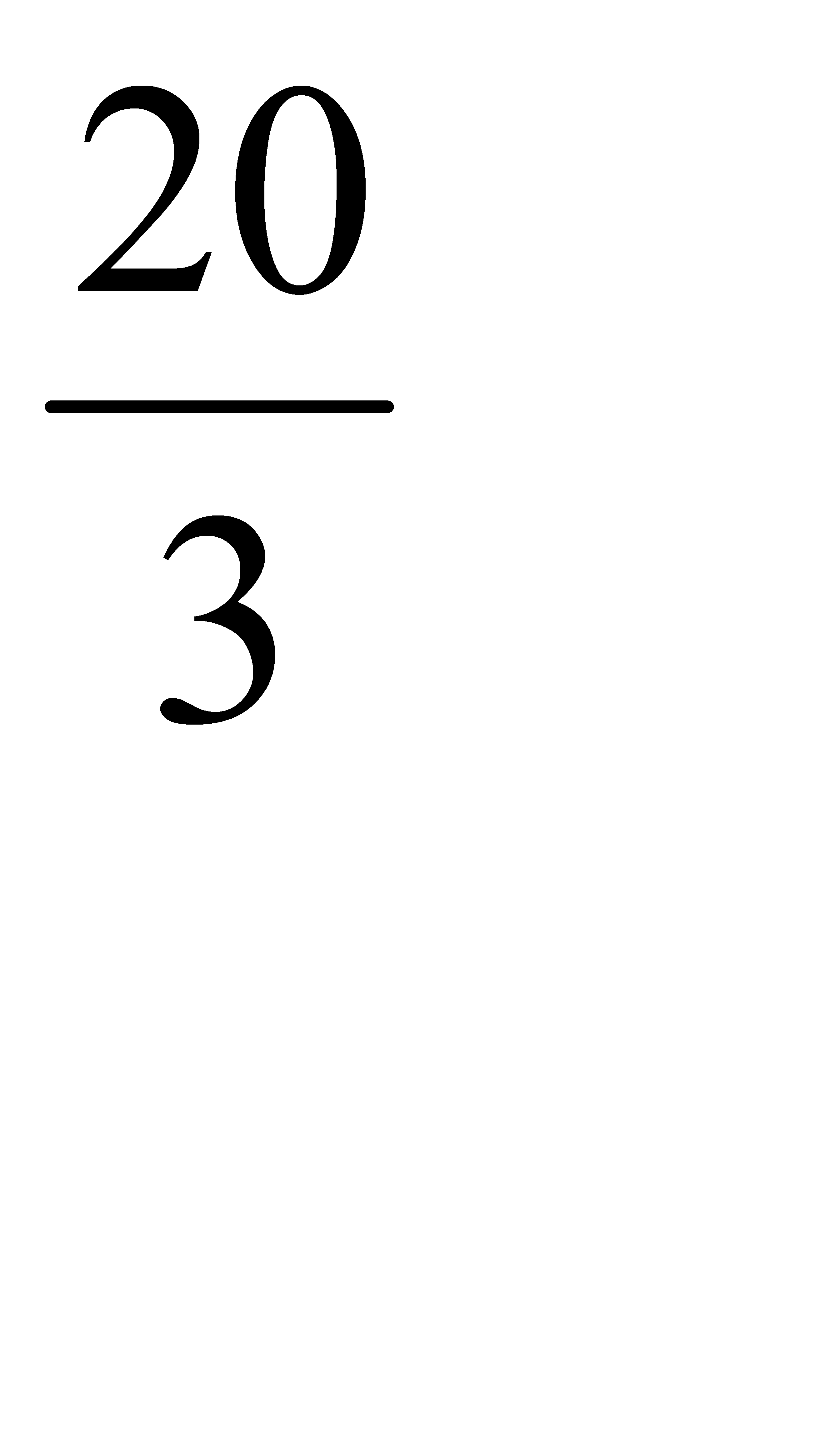 ↑ ↑
| – 
| 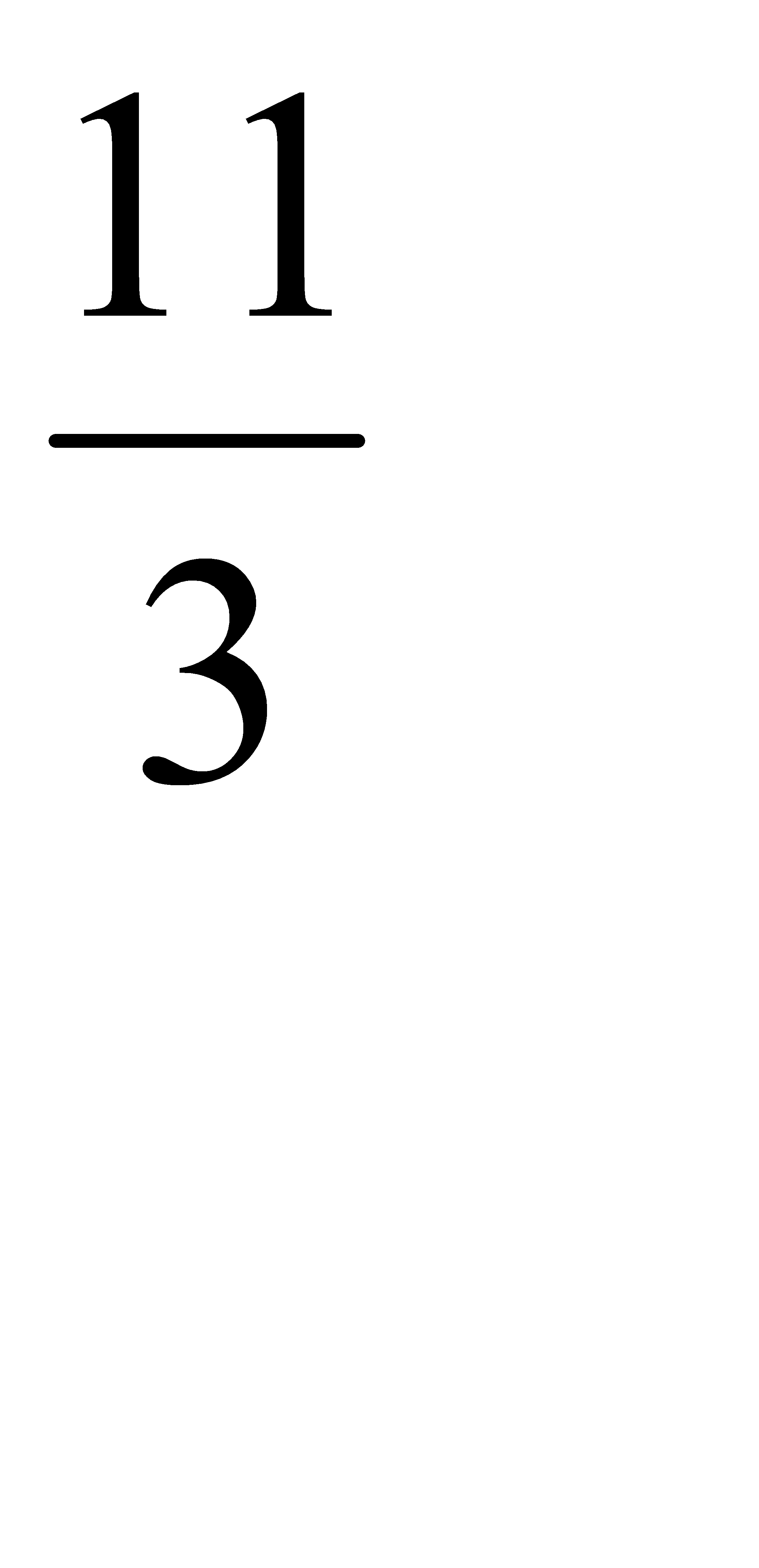
| ||||||
| Таблица 2 | x3 | 
| – 
| ||||||
| x5 | 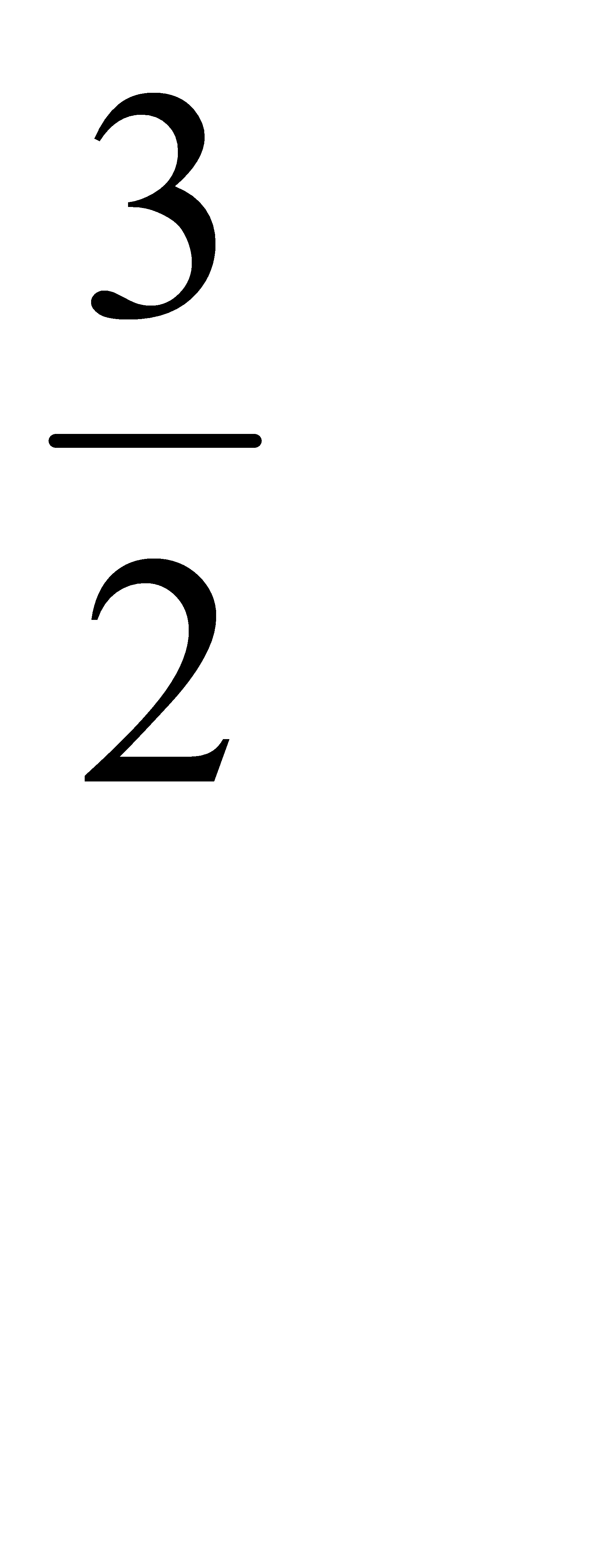
| – 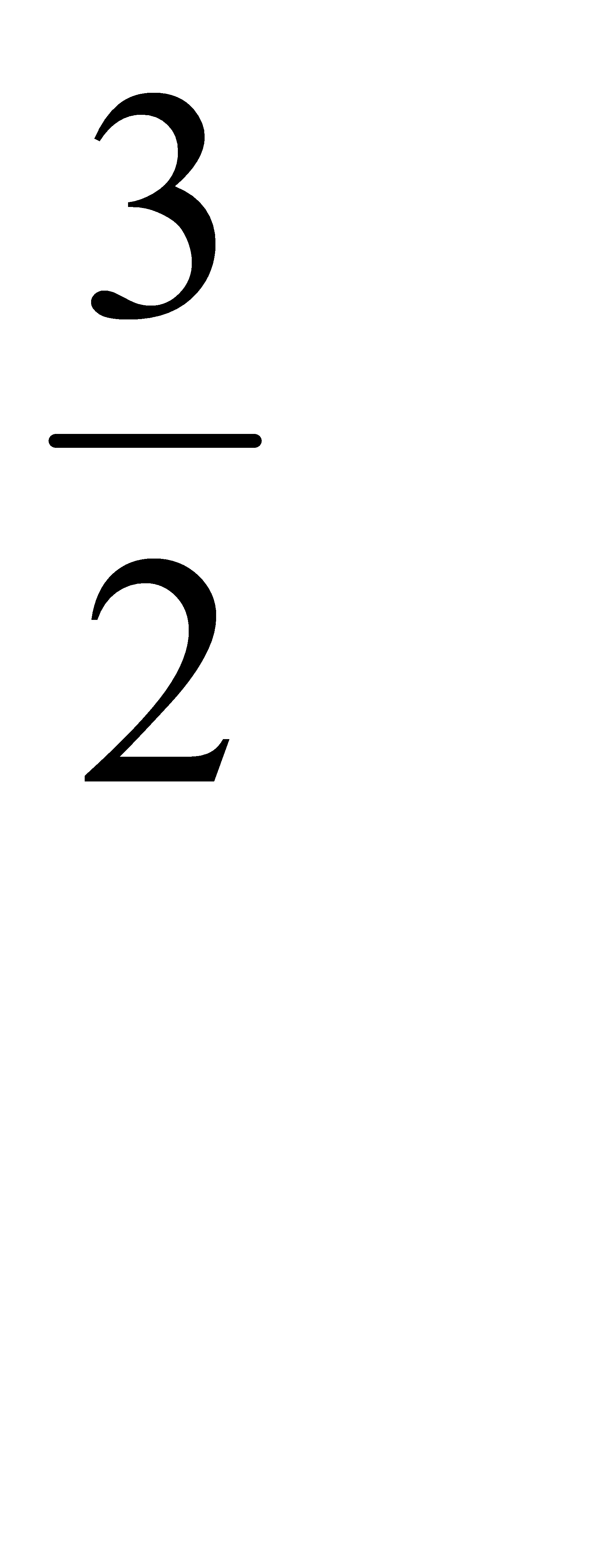
| |||||||
| x1 | 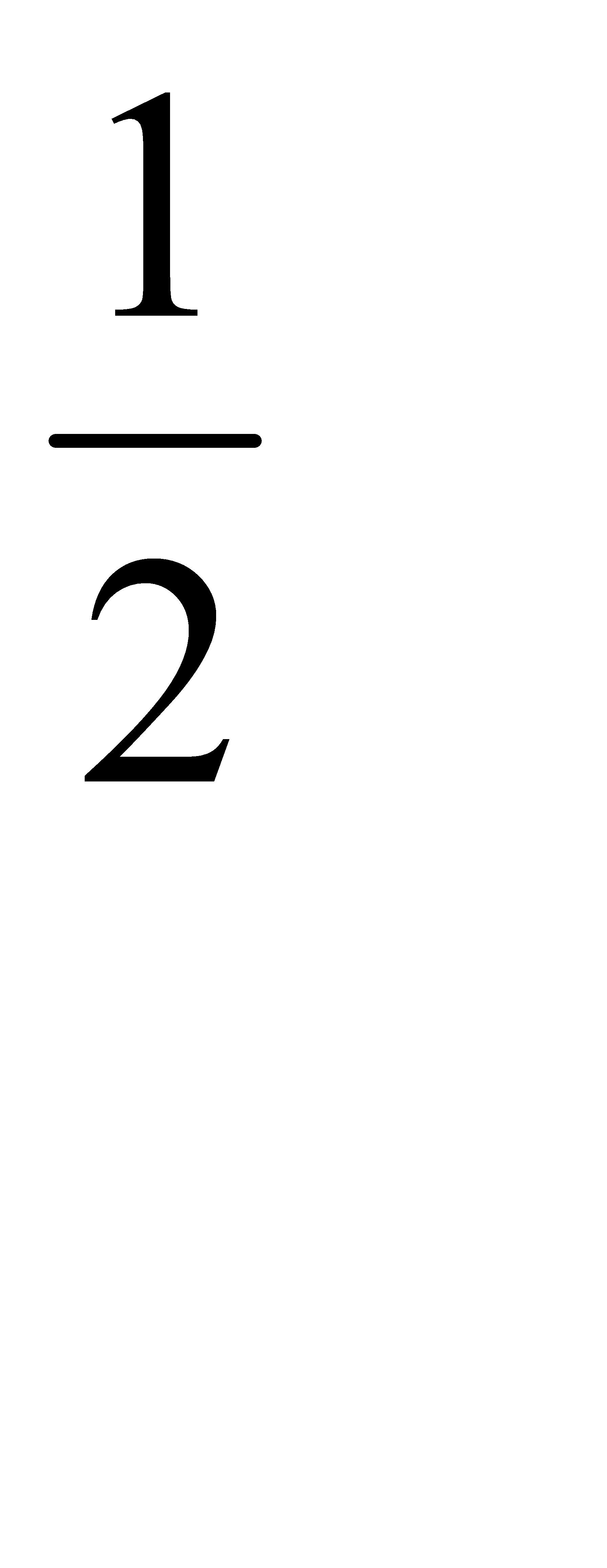
| – 
| 
| ||||||
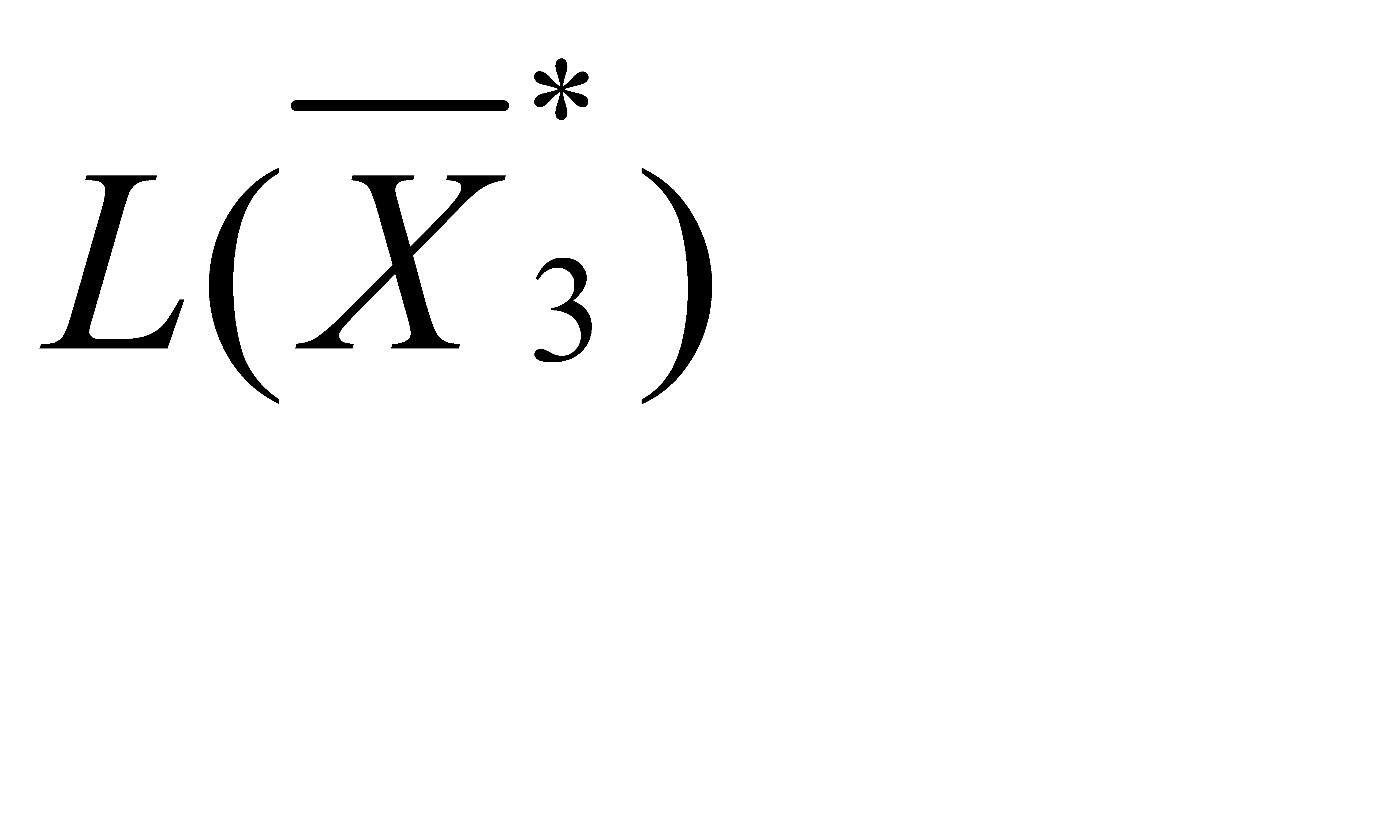
|
Тема: Двойственная задача к задаче планирования торговли
Каждой задаче линейного программирования можно сопоставить другую задачу, называемую двойственной или сопряженной по отношению к исходной или прямой. Составим двойственную задачу к задаче планирования товарооборота (2.1) – (2.3), которую будем называть прямой.
Обозначим yi ( 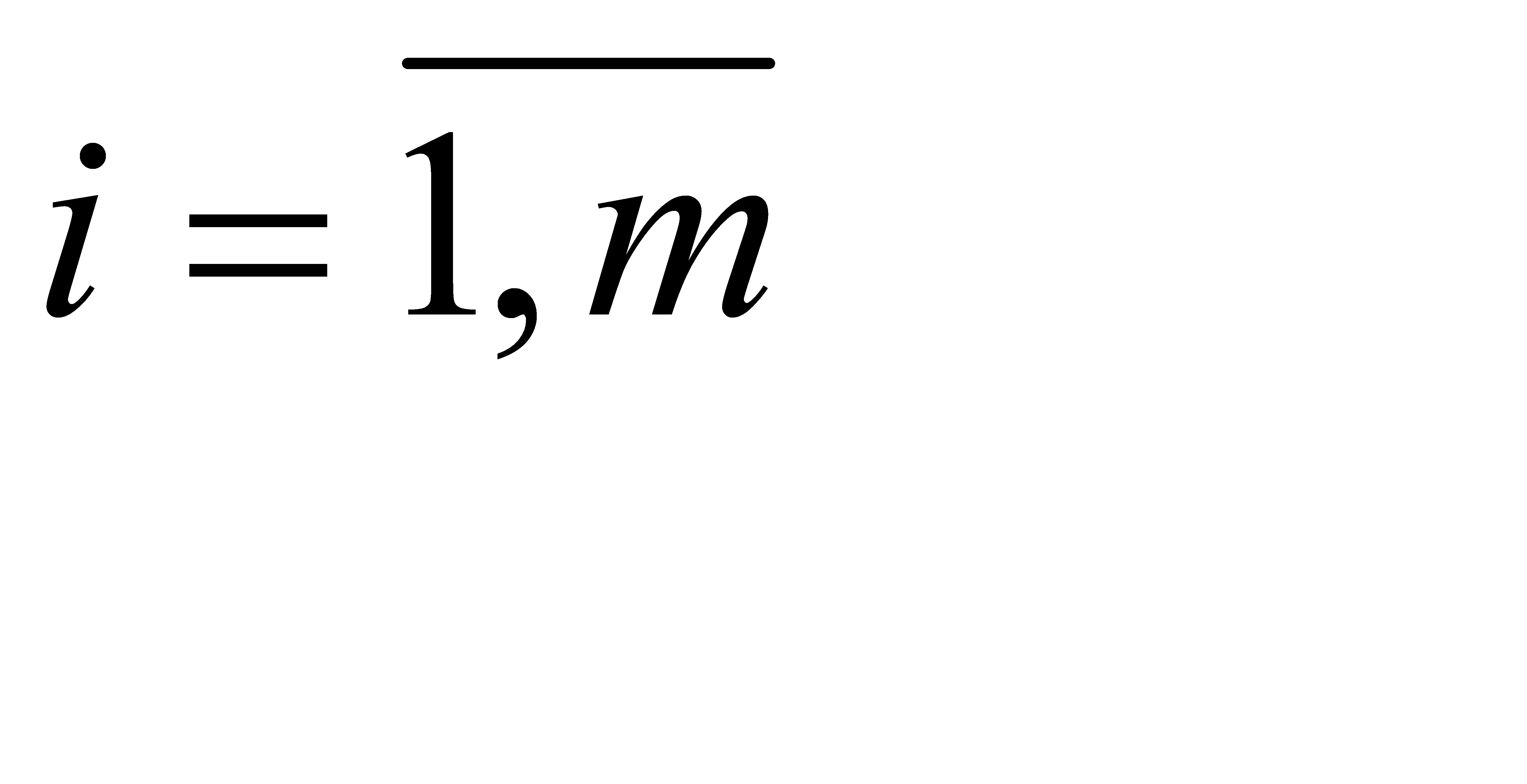 ) – двойственная оценка (неявная стоимость) единицы i-го ресурса. Тогда двойственная задача к задаче планирования торговли формулируется следующим образом:
) – двойственная оценка (неявная стоимость) единицы i-го ресурса. Тогда двойственная задача к задаче планирования торговли формулируется следующим образом:
Требуется определить оценку единицы каждого вида ресурса, чтобы при заданных объемах ресурса bi, нормах их расхода aij и показателях прибыли cj, общая стоимость ресурсов, затраченных на организацию торгового процесса, была бы минимальной.
Запишем математическую модель двойственной задачи к задаче линейного программирования (2.1) – (2.3).
Определить 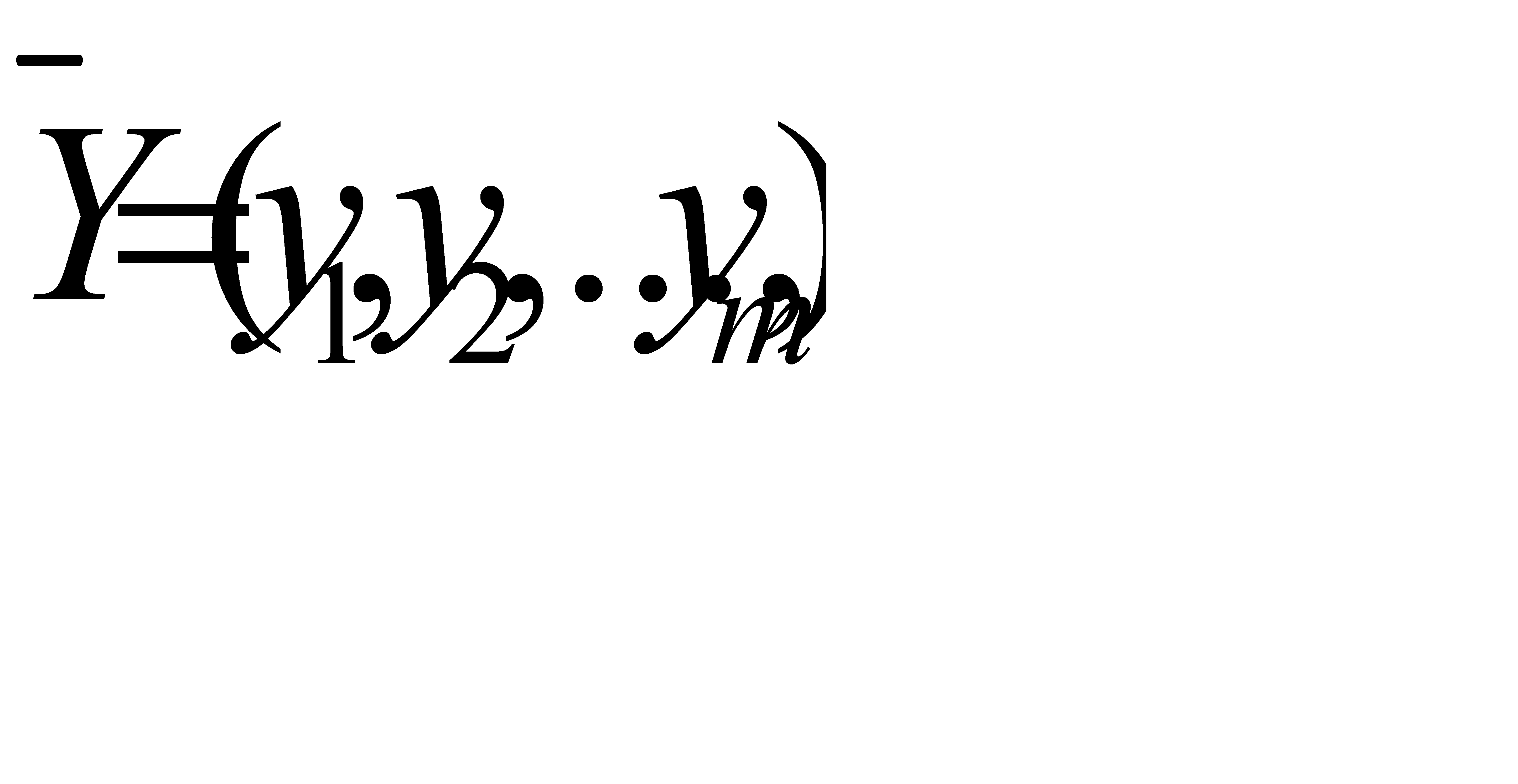 , который удовлетворяет условиям
, который удовлетворяет условиям
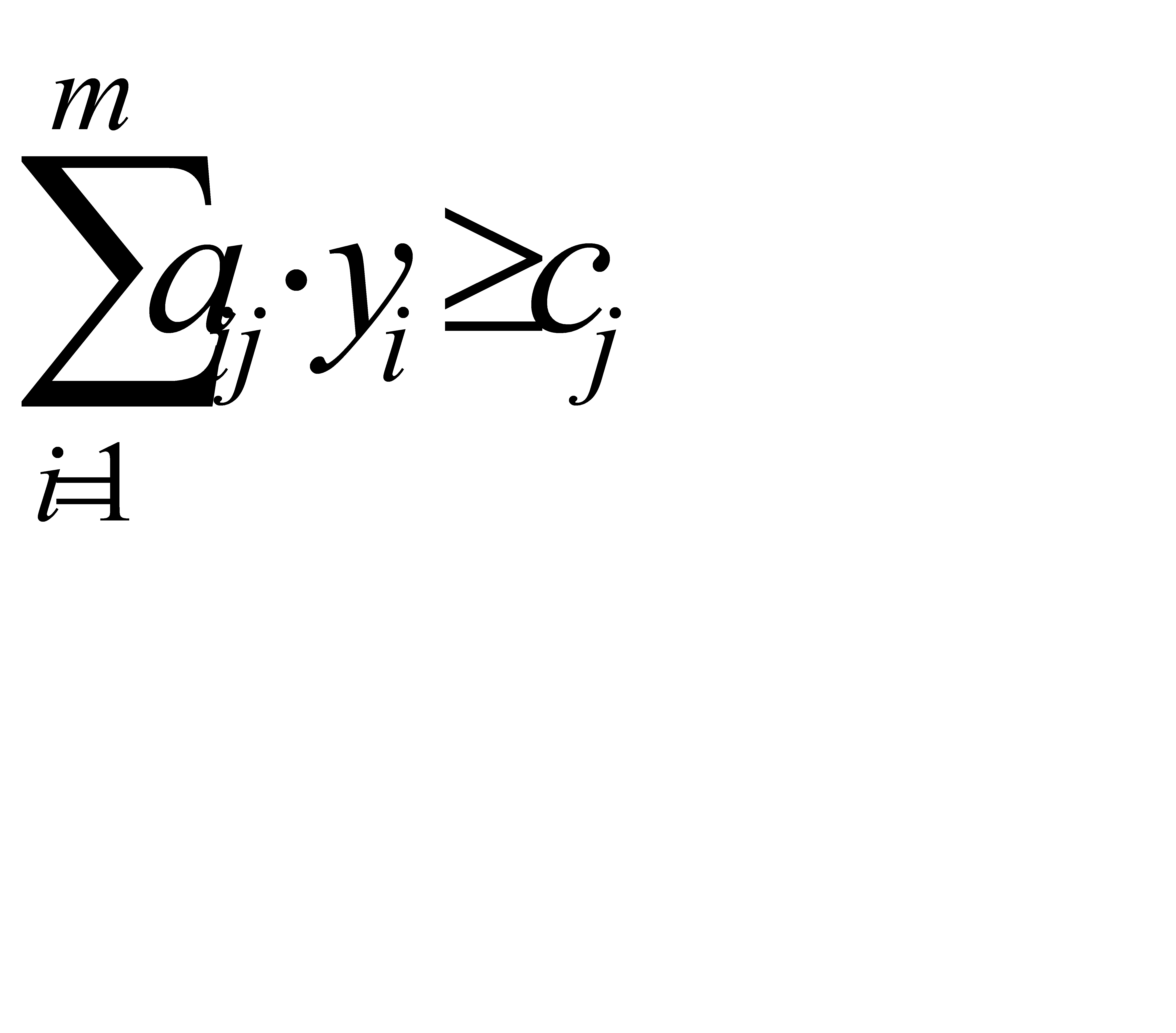 ,
, 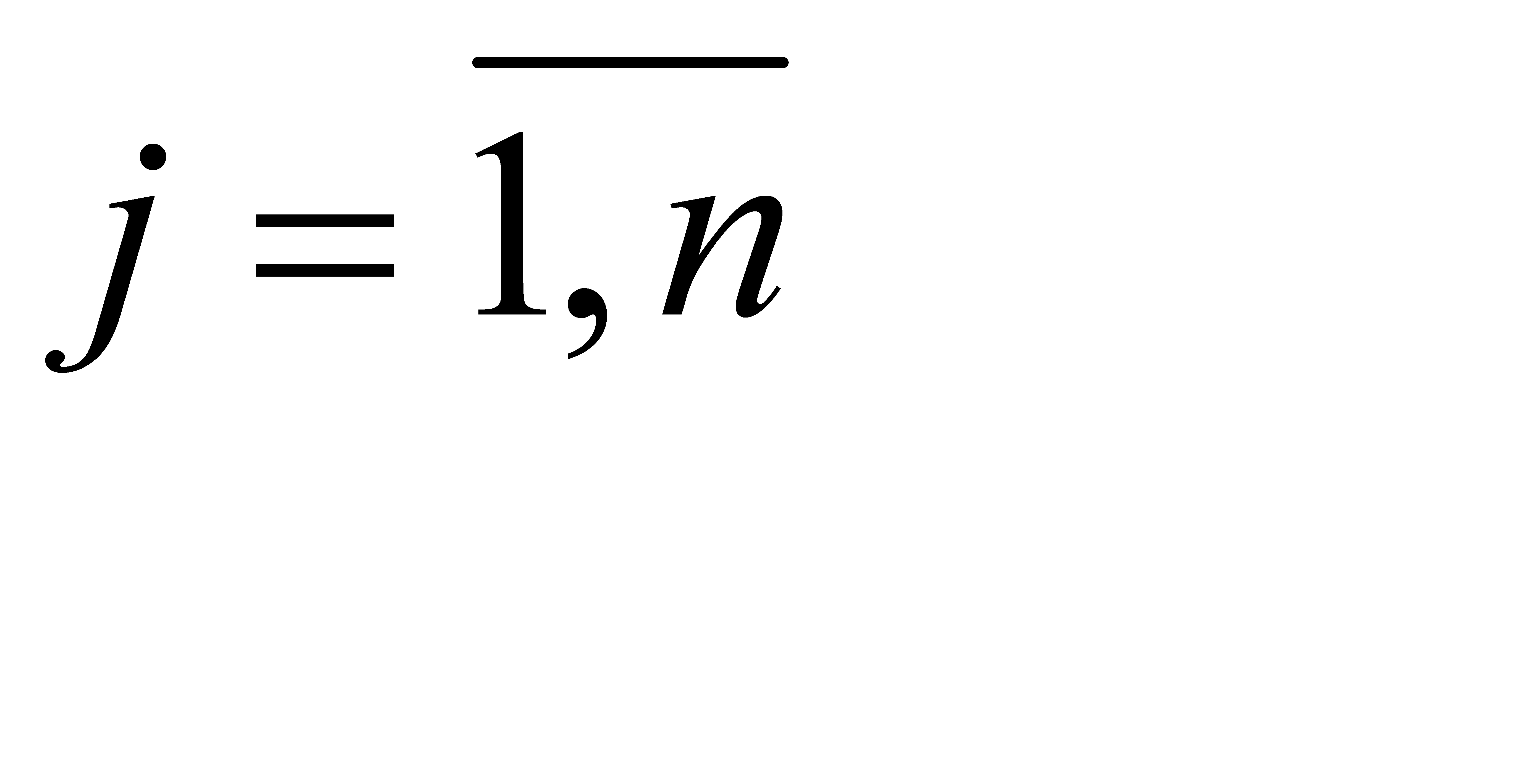 (3.1)
(3.1)
yi ≥ 0, 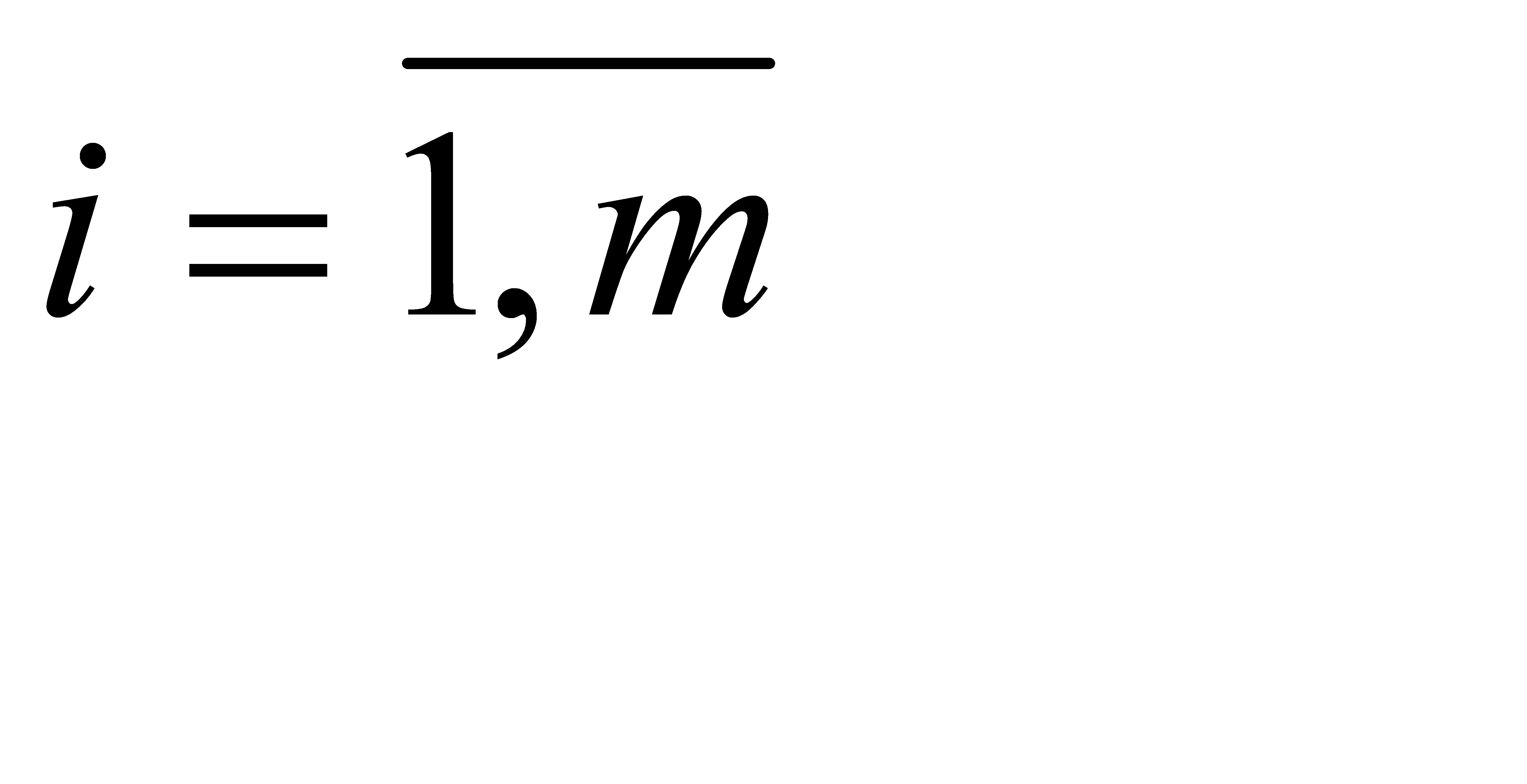 (3.2)
(3.2)
и доставляет минимальное значение целевой функции
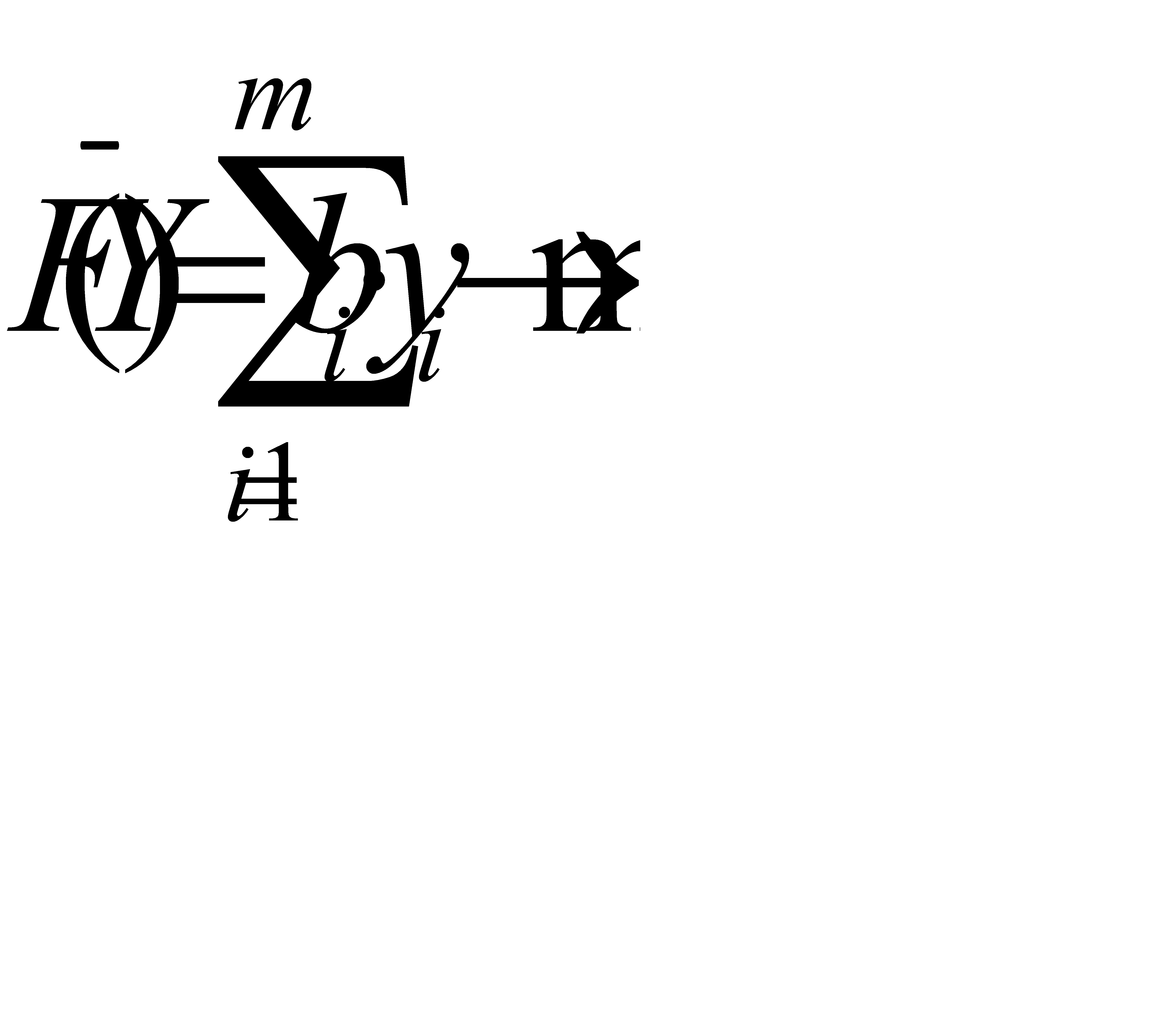 (3.3)
(3.3)
Ограничения (3.1) показывают, что оценка (стоимость) всех ресурсов, затраченных на продажу единицы j группы товаров, должна быть не меньше прибыли, получаемой от продажи единицы j группы товаров, а общая стоимость всех ресурсов (3.3) должна быть минимальной.
Задачи (2.1) – (2.3) и (3.1) – (3.3) представляют симметричную пару двойственных задач, так как системы ограничений заданы неравенствами и на переменные xj и yi накладывается условие неотрицательности.
Для симметричной пары задач двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Число переменных в двойственной задаче равно числу ограничений в прямой задаче.
2. Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограничений прямой путем транспонирования.
3. Если система ограничений прямой задачи задана неравенствами смысла «≤», то система ограничений двойственной задачи записывается неравенствами смысла «≥».
4. Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.
5. Если целевая функция прямой задачи задается на максимум, то целевая функция двойственной задачи – на минимум.
6. Коэффициентами функции цели двойственной задачи являются свободные члены системы ограничений прямой задачи.
7. На каждую переменную двойственной задачи накладывается условие неотрицательности.
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении оптимального плана одной из задач находится решение и другой задачи. Существующие зависимости между решениями прямой и двойственной задач характеризуются теоремами двойственности.
Теорема 1. Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т.е. 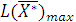 =
= 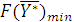 .
.
Теорема 2. План прямой задачи 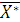 и план двойственной задачи
и план двойственной задачи 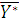 являются оптимальными только тогда, если для любого
являются оптимальными только тогда, если для любого 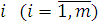 и
и 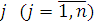 выполняются равенства:
выполняются равенства:
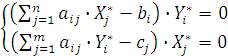 (3.4)
(3.4)
Из (3.4) следует, что для оптимальных планов пары двойственных задач необходимо и достаточно выполнение следующих условий:
1. Если для некоторого 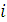
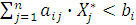 , то
, то 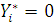 ;
;
2. Если для некоторого 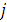
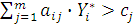 , то
, то 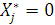 .
.
Теорема 3. Если исходная задача имеет оптимальный план 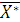 , то оптимальный план двойственной задачи можно определить с помощью следующего соотношения:
, то оптимальный план двойственной задачи можно определить с помощью следующего соотношения:
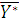 = Сб∙А−1 (3.5)
= Сб∙А−1 (3.5)
где Сб – коэффициенты целевой функции базисных переменных, вошедших в оптимальный план исходной задачи;
А−1 - обратная матрица к матрице, составленной из векторов, вошедших в оптимальный план.
Таким образом, если найти оптимальный план исходной задачи, то используя соотношение (3.5) можно определить оптимальный план двойственной задачи. Поскольку в системе уравнений исходной задачи (2.4) среди векторов 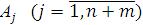 имеются m единичных, то матрица А−1 расположена в первых m строках оптимальной симплексной таблицы в столбцах единичных векторов. Тогда нет необходимости определять оптимальный план двойственной задачи умножением Сб на А−1, поскольку компоненты этого плана совпадают с соответствующими элементами индексной (m + 1)-й строки столбцов единичных векторов.
имеются m единичных, то матрица А−1 расположена в первых m строках оптимальной симплексной таблицы в столбцах единичных векторов. Тогда нет необходимости определять оптимальный план двойственной задачи умножением Сб на А−1, поскольку компоненты этого плана совпадают с соответствующими элементами индексной (m + 1)-й строки столбцов единичных векторов.
Пример.
В качестве прямой задачи используем задачу (2.7) – (2.9), которая решена симплексным методом. Составим к данной задаче двойственную и запишем её оптимальный план.
Требуется определить 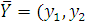 ,
, 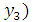 , который удовлетворяет условиям
, который удовлетворяет условиям
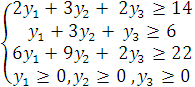
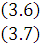
и доставляет минимальное значение целевой функции
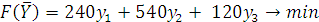 (3.8)
(3.8)
Задачи (2.7) – (2.9) и (3.6) – (3.8) образуют симметричную пару двойственных задач. Решение прямой задачи определяет оптимальный объем и структуру товарооборота торгового предприятия, а решение двойственной – оптимальную систему оценок ресурсов, используемых для реализации товаров.
Установим сопряженные пары переменных прямой и двойственной задач. В первой строке запишем переменные xj по порядку номеров (сначала основные, затем – дополнительные), во второй строке – переменные двойственной задачи, оптимальные значения которых получены в индексной (m + 1)-й строке таблицы 3.3.
1. x1 x2 x3 x4 x5 x6
основные дополнительные
2. 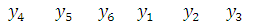
дополнительные основные
Согласно сопряженным парам переменных из решения прямой задачи получаем решение двойственной, не решая её, и наоборот.
Таким образом, оптимальный план двойственной задачи (см.таблицу 3.3) к задаче планирования товарооборота равен:
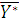 = (2, 0, 5, 0, 1, 0),
= (2, 0, 5, 0, 1, 0), 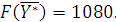
Анализ оптимального плана двойственной задачи
В оптимальном плане словные двойственные оценки единицы ресурсов I и III видов отличны от нуля ( 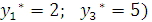 . Ресурсы I и III видов в оптимальном плане прямой задачи используются полностью, так как дополнительные переменные (
. Ресурсы I и III видов в оптимальном плане прямой задачи используются полностью, так как дополнительные переменные ( 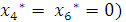 .
.
Двойственная оценка единицы ресурса II вида равна нулю 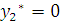 . Этот вид ресурса не полностью используется при оптимальном плане реализации товаров
. Этот вид ресурса не полностью используется при оптимальном плане реализации товаров 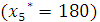 .
.
Таким образом, двойственные оценки в оптимальном плане больше нуля у тех видов ресурсов, которые полностью используются при реализации товаров. Поэтому данные оценки определяют дефицитность ресурса предприятия, а её величина показывает, на сколько возрастет максимальное значение целевой функции прямой задачи при увеличении количества соответствующего вида ресурса на единицу. Например, увеличение ресурса III вида на 1 м2 приведет к получению нового оптимального плана, при котором прибыль от реализации товаров возрастет на 5 т.руб. и станет равной: 1080 + 5 = 1085 тыс.руб. При этом коэффициенты, стоящие в столбце переменной x6 таблицы 3.3, показывают, что указанное увеличение прибыли достигается за счет увеличения продажи товаров I группы на  ед., уменьшения продажи товаров III группы на
ед., уменьшения продажи товаров III группы на  ед. . Аналогично можно найти новый оптимальный товарооборота при изменении дефицитного ресурса I вида.
ед. . Аналогично можно найти новый оптимальный товарооборота при изменении дефицитного ресурса I вида.
При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи (3.6) получаем
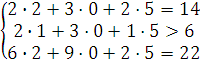
Второе ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка ресурса, используемого для реализации единицы товара II группы, выше прибыли. Следовательно, продавать товары II группы невыгодно и их продажа не предусмотрена оптимальным планом прямой задачи 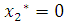 . Первое и третье ограничения двойственной задачи являются равенствами. Это означает, что двойственные оценки ресурса, используемого для продажи единицы товара I и III группы, равны в точности прибыли, получаемой от их реализации. Поэтому продажа данных групп товаров экономически целесообразна и предусмотрена оптимальным планом прямой задачи.
. Первое и третье ограничения двойственной задачи являются равенствами. Это означает, что двойственные оценки ресурса, используемого для продажи единицы товара I и III группы, равны в точности прибыли, получаемой от их реализации. Поэтому продажа данных групп товаров экономически целесообразна и предусмотрена оптимальным планом прямой задачи.
Задачи
Используя вариант контрольного задания № 70-138, необходимо:
− к прямой задаче планирования товарооборота составить двойственную (записать математическую модель);
− используя оптимальный план прямой задачи, установить сопряженные пары переменных прямой и двойственной задач;
− согласно сопряженным парам переменных из оптимального плана прямой задачи записать оптимальный план двойственной задачи и дать анализ двойственных оценок.
Дата добавления: 2017-05-18; просмотров: 1042;
