Термодинамические процессы в одноступенчатом идеальном компрессоре.

Теоретический рабочий процесс. Компрессор (рис.6) состоит из цилиндра 1 с поршнем 2, который при помощи кривошипно-шатунного механизма 5, соединенного с валом, совершает возвратно- поступательное движение. Вал получает вращательное движение от электродвигателя или двигателя другого типа. Для всасывания и нагнетания газа имеются соответственно всасывающий 3 и нагнетательный 4 клапаны. Оба клапана самодействующие, открываются и закрываются под действием разности давлений в цилиндре и трубопроводе.

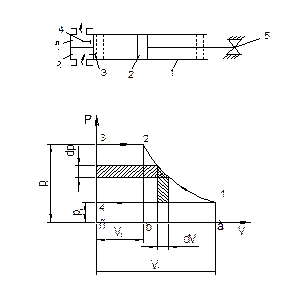
Рис. 6. Принципиальная схема компрессора и теоретический рабочий процесс

При рассмотрении теоретического процесса делают следующие допущения: объем всасываемого газа V_вс равен теоретической объемной подаче V_т, т.е. отсутствует мертвое пространство – пространство между крышкой цилиндра и поршнем в крайнем положении; отсутствует трение поршня о стенки цилиндра; отсутствует гидравлическое сопротивление всасывающих и нагнетательных клапанов, т. е. в процессах всасывания и нагнетания давление газа не изменяется.

Теоретический рабочий процесс в компрессоре (рис.7 ) представлен в виде индикаторной диаграммы, которая показывает изменение давления и рабочего объема в цилиндре по ходу поршня.

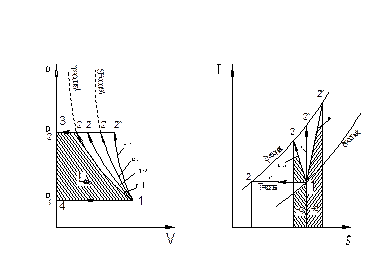
Рис.7. Процесс сжатия газа в теоретическом цикле

При движении поршня вправо происходит всасывание газа в цилиндр компрессора по линии 4-1 при постоянном давлении Р₁; при обратном движении поршня газ сжимается в процессе 1-2 от начального давления Р₁ до конечного Р₂, а затем происходит выталкивание газа по линии 2-3 при постоянном давлении Р₂. так как в рассматриваемом теоретическом компрессоре отсутствует мертвое пространство, то линия 3-4 совпадает с осью координат, т. е. в левой мертвой точке давление меняется мгновенно от Р₂ до Р₁. кроме того, вследствие предполагаемого отсутствия гидравлического сопротивления всасывающего и нагнетательного клапанов линии 4-1 и 2-3 совпадают соответственно с линиями Р₁=const и Р₂=const.

При всасывании и нагнетании объем газа, заключенного в цилиндре, изменяется вместе с его массовым количеством, но его удельные объемы υ₁ и υ₂ остаются постоянными. Поэтому цикл компрессора, изображенный в координатах V-р, не может быть представлен в координатах υ-р.

В зависимости от условий процесс сжатия газа в теоретическом цикле может протекать по изотерме, адиабате или политропе, вследствие чего цикл компрессора называют соответственно изотермическим, адиабатным или политропным.

Процессы всасывания и нагнетания не являются термодинамическими, так как для идеального компрессора они не изменяют термодинамические параметры газа, а при изменении объема цилиндра происходят механические процессы его заполнения газом и опорожнения.

Работа L_к, расходуемая на осуществление теоретического цикла, т.е. на сжатие V м³ газа от давления Р₁ до давления Р₂, выразится в виде алгебраической суммы трех работ: работы всасывания L_вс, работы сжатия L_сж и работы нагнетания L_н. работу всасывания принимают положительной, так как при всасывании увеличивается объем газа в цилиндре, а работы сжатия и нагнетания, связанные с уменьшением объема газа в цилиндре, - отрицательными.

В связи с этим, можно записать:

L_вс=р₁∙F∙S₁=p₁∙V₁

L_н=-р₂∙F∙S₂=p₂∙V₂

где F – площадь сечения поршня; S₁, S₂, V₁, V₂ – ход поршня и объем цилиндра при всасывании и при нагнетании соответственно, м, м³.

А работа сжатия:

L_сж= 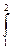р∙dV

Результирующая работа за цикл выражается суммой:

L_к=L_вс+L_сж+L_н

Величина работы компрессора изменяется в зависимости от термодинамического характера процесса сжатия.

В изотермическом процессе сжатия идеального газа давление и удельный объем связаны уравнением:

p₁∙υ₁=p₂∙υ₂

Тогда работа компрессора для произвольной массы газа в этом случае равна работе сжатия:

L_к.из.=L_сж=-р₁∙V₁∙ln(υ₁/υ₂) = -m∙R∙T∙ln(p₂/p₁)

или для одного килограмма газа:

L_к.из.=-р₁∙υ₁∙ln(υ₁/υ₂)= -R∙T∙ln(p₂/p₁)

В адиабатном процессе сжатия идеального газа между давлением и удельным объемом существует соотношение:

р∙υ^k=const, т.е. р₁∙υ₁^k=p₂∙υ₂^k

Значение работы адиабатного сжатия:

l_сж=[1/(k-1)]∙(p₁∙υ₁ – p₂∙υ₂)

Удельная работа компрессора при адиабатном процессе сжатии:

l_к.ад.=[k/(k-1)]∙(p₁∙υ₁-p₂∙υ₂) = [k/(k-1)]∙R∙(T₁-T₂)

А так как величина k=c_p/c_υ больше единицы, то при адиабатном процессе работа компрессора всегда больше, чем при изотермическом.

Для политропного процесса сжатия газа удельный объем и давление связаны уравнением:

р∙υⁿ=const, т.е. р₁∙υ₁ⁿ=p₂∙υ₂ⁿ

Температура газа в конце сжатия в политропном процессе равна:

T₂=T₁∙(p₂/p₁)^(n-1)/n

Тогда удельная работа политропного сжатия :

l_сж=[1/(n-1)]∙(p₁∙υ₁-p₂∙υ₂)

Удельная работа компрессора:

l_к.пол.=[n/(n-1)]∙(p₁∙υ₁-p₂∙υ₂)