Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 10 страница

Задачи

23.1. Плоская световая волна с длиной волны 0,6 мкм падает нормально на диафрагму с круг­лым отверстием диаметром 1 см. Определить расстояние от точки наблюдения до отвер­стия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля. [1) 20,8 м; 2) 13,9 м]

23.2. Дифракционная картина наблюдается на расстоянии 1 м от точечного источника монохро­матического света (l=0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционной картины на экране будет наиболее темным. [0,5 мм]

23.3. На щель шириной 0,2 мм падает нормально монохроматический свет с длиной волны 0,5 мкм. Экран, на котором наблюдается дифракционная картина, расположен параллель­но щели на расстоянии 1 м. Определить расстояние между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума. [5 мм]

23.4. Определить число штрихов на 1 мм дифракционной решетки, если углу p/2 соответствует максимум пятого порядка для монохроматического света с длиной волны 0,5 мкм. [400 мм^–1]

23.5. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстоянием 0,28 нм между его атомными плоскостями. Определить длину волны рентгеновского излучения, если под углом 30° к плоскости грани наблюдается дифракционный максимум второго порядка. [140 пм]

23.6. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (l₁=578 нм и l₂=580 нм). Длина решетки 1 см. [34,6 мкм]

Глава 24 Взаимодействие электромагнитных волн с веществом

§ 185. Дисперсия света

Дисперсией света называется зависимость показателя преломления n вещества от частоты n (длины волны l) света или зависимость фазовой скорости v световых волн (см. § 154) от его частоты n. Дисперсия света представляется в виде зависимости

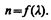(185.1)

Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые экспериментальные наблюдения дисперсии света принад­лежат И. Ньютону (1672 г.).

Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления п (рис. 268) под углом a₁. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол j. Из рисунка следует, что

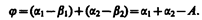(185.2)

Предположим, что углы А иa₁ малы, тогда углы a₂, b₁ и b₂ будут также малы и вместо синусов этих углов можно воспользоватьсяих значениями. Поэтому a₁/b₁=n, b₂/a₂=1/n, а таккак b₁+b₂=А, то a₂=b₂n=n(A–b₁)=n (A–a₁/n)=nA–a₁, откуда

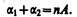(185.3)

Из выражений (185.3) и (185.2) следует, что

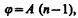(185.4)

т. е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы.

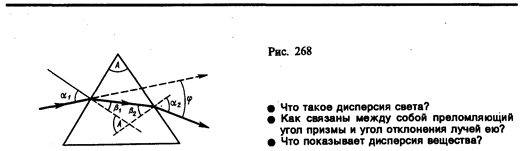
Из выражения (185.4) вытекает, что угол отклонения лучей призмой зависит от величины n–1, а n — функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т. е. пучок белого света за призмой разлагается в спектр, что и наблюдалось И. Ньютоном. Таким образом, с помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.

Рассмотрим различия в дифракционном и призматическом спектрах.

1. Дифракционная решетка разлагает падающий свет непосредственно по длинам воли (см. (180.3)), поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n=f(l) (185.1).

2. Составные цвета в дифракционном и призматическом спектрах располагаются различно. Из (180.3) следует, что в дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается (рис. 269). Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые.

Величина

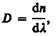
называемая дисперсией вещества, показывает, как быстро изменяется показатель прело­мления с длиной волны. Из рис. 269 следует, что показатель преломления для прозрач­ных веществ с уменьшением длины волны увеличивается; следовательно, величина dn/dl по модулю также увеличивается с уменьшением l. Такая дисперсия называется нормальной. Как будет показано ниже, ход кривой n(l) — кривой дисперсии — вблизи линий и полос поглощения будет иным: n уменьшается с уменьшением l. Такой ход зависимости n от l называется аномальной дисперсией.

На явлении нормальной дисперсии основано действие призменных спектрографов. Несмотря на их некоторые недостатки (например, необходимость градуировки, различ­ная дисперсия в разных участках спектра) при определении спектрального состава света, призменные спектрографы находят широкое применение в спектральном анали­зе. Это объясняется тем, что изготовление хороших призм значительно проще, чем изготовление хороших дифракционных решеток. В призменных спектрографах также легче получить большую светосилу.

§ 186. Электронная теория дисперсии светя

Из макроскопической электромагнитной теории Максвелла следует, что абсолютный показатель преломления среды

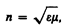
где e — диэлектрическая проницаемость среды, m — магнитная проницаемость. В оп­тической области спектра для всех веществ m»1, поэтому

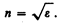(186.1)

Из формулы (186.1) выявляются некоторые противоречия с опытом: величина n, являясь переменной (см. § 185), остается в то же время равной определенной постоян­ной 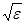. Кроме того, значения n, получаемые из этого выражения, не согласуются с опытными значениями. Трудности объяснения дисперсии света с точки зрения элект­ромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромаг­нитных волн с заряженными частицами, входящими в состав вещества и совершающи­ми вынужденные колебания в переменном электромагнитном поле волны.

Применим электронную теорию дисперсии света для однородного диэлектрика, предположив формально, что дисперсия света является следствием зависимости e от частоты w световых волн. Диэлектрическая проницаемость вещества, по определению (см. (88.6) и (88.2)), равна

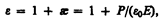
где { — диэлектрическая восприимчивость среды, e₀ — электрическая постоянная, Р — мгновенное значение поляризованности. Следовательно,

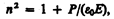(186.2)

т.е. зависит от Р. В данном случае основное значение имеет электронная поляризация, т.е. вынужденные колебания электронов под действием электрической составляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока (n » 10¹⁵ Гц).

В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные с ядром электроны —оптические электроны. Для простоты рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р=ех, где е — заряд электрона, х — смещение электрона под действием элект­рического поля световой волны. Если концентрация атомов в диэлектрике равна n₀, то мгновенное значение поляризованности

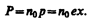(186.3)

Из (186.2) и (186.3) получим

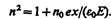(186.4)

Следовательно, задача сводится к определению смещения х электрона под действием внешнего поля Е. Поле световой волны будем считать функцией частоты w, т. е. изменяющимся по гармоническому закону: Е = Е₀ cos w t.

Уравнение вынужденных колебаний электрона (см. §147) для простейшего случая (без учета силы сопротивления, обусловливающей поглощение энергии падающей волны) запишется в виде

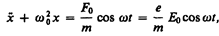(186.5)

где F₀ = еЕ₀ — амплитудное значение силы, действующей на электрон со стороны поля волны, 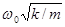— собственная частота колебаний электрона, т — масса электрона. Решив уравнение (186.5), найдем e = n² в зависимости от констант атома (е, т, w₀) и частоты w внешнего поля, т.е. решим задачу дисперсии. Решение уравнения (186.5) можно записать в виде

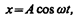(186.6)

где

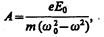(186.7)

в чем легко убедиться подстановкой (см. (147.8)). Подставляя (186.6) и (186.7) в (186.4), получим

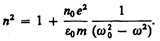(186.8)

Если в веществе имеются различные заряды е_i, совершающие вынужденные колебания с различными собственными частотами w_0i, то

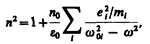(186.9)

где т, — масса i-го заряда.

Из выражений (186.8) и (186.9) вытекает, что показатель преломления n зависит от частоты w внешнего поля, т. е. полученные зависимости действительно подтверждают явление дисперсии света, хотя и при указанных выше допущениях, которые в даль­нейшем надо устранить. Из выражений (186.8) и (186.9) следует, что в области от w = 0 до w = w₀ n² больше единицы и возрастает с увеличением w (нормальная дисперсия); при w = w₀ n² = ±¥; в области от w = w₀ до w = ¥ n² меньше единицы и возрастает от –¥ до 1 (нормальная дисперсия). Перейдя от n² к n, получим, что график зависимости n от w имеет вид, изображенный на рис. 270. Такое поведение n вблизи w₀ — результат допущения об отсутствии сил сопротивления при колебаниях электро­нов. Если принять в расчет и это обстоятельство, то график функции n(w) вблизи w₀ задастся штриховой линией АВ. Область АВ — область аномальной дисперсии (n убывает при возрастании w), остальные участки зависимости n от w описывают нормальную дисперсию (n возрастает с возрастанием w).

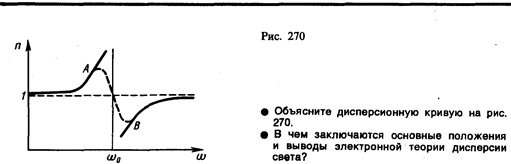
Российскому физику Д. С. Рождественскому (1876—1940) принадлежит классичес­кая работа по изучению аномальной дисперсии в парах натрия. Он разработал ин­терференционный метод для очень точного измерения показателя преломления паров и экспериментально показал, что формула (186.9) правильно характеризует зависи­мость n от w, а также ввел в нее поправку, учитывающую квантовые свойства света и атомов.

§ 187. Поглощение (абсорбция) света

Поглощением (абсорбцией) света называется явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии. В результате поглощения интенсивность света при прохождении через вещество уменьшается.

Поглощение света в веществе описывается законом Бугера*:

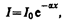(187.1)

где I₀ и I — интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающего вещества толщиной х, a —коэффициент поглощения, зависящий от длины волны света, химической природы и состояния вещества и не зависящий от интенсивности света. При х=1/a интенсивность света I по сравнению с I₀ уменьшается в е раз.

* П. Бугер (1698—1758) — французский ученый.

Коэффициент поглощения зависит от длины волны l (или частоты w) и для различных веществ различен. Например, одноатомные газы и пары металлов (т.е. вещества, в которых атомы расположены на значительных расстояниях друг от друга и их можно считать изолированными) обладают близким к нулю коэффициентом поглощения и лишь для очень узких спектральных областей (примерно 10^–12—10^–11 м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молеку­лах, характеризуется полосами поглощения (примерно 10^–10—10^–7 м).

Коэффициент поглощения для диэлектриков невелик (примерно 10^–3—10^–5 см^–1), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда a резко возрастает, и наблюдаются сравнительно широкие полосы поглощения, т.е. диэлектрики имеютсплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлени­ем резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика.

Коэффициент поглощения для металлов имеет большие значения (примерно 10³—10⁵ см^–1) и поэтому металлы являются непрозрачными для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превраща­ясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.

На рис. 271 представлены типичная зависимость коэффициента поглощения a от длины волны света l и зависимость показателя преломления n от l в области полосы поглощения. Из рисунка следует, что внутри полосы поглощения наблюдается ано­мальная дисперсия (n убывает с уменьшением l). Однако поглощение вещества должно быть значительным, чтобы повлиять на ход показателя преломления.

Зависимостью коэффициента поглощения от длины волны объясняется окрашенность поглощающих тел. Например, стекло, слабо поглощающее красные и оранжевые лучи и сильно поглощающее зеленые и синие, при освещении белым светом будет казаться красным. Если на такое стекло направить зеленый и синий свет, то из-за сильного поглощения света этих длин волн стекло будет казаться черным. Это явление используется для изготовлениясветофильтров, которые в зависимости от химического состава (стекла с присадками различных солей, пленки из пластмасс, содержащие красители, растворы красителей и т. д.) пропускают свет только определенных длин волн, поглощая остальные. Разнообразие пределов селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающееся в окружающем мире.

Явление поглощения широко используется в абсорбционном спектральном анализе смеси газов, основанном на измерениях спектров частот и интенсивностей линий (полос) поглощения. Структура спектров поглощения определяется составом и стро­ением молекул, поэтому изучение спектров поглощения является одним из основных методов количественного и качественного исследования веществ.

§ 188. Эффект Доплера

Эффект Доплера в акустике (см. § 159) объясняется тем, что частота колебаний, воспринимаемых приемником, определяется скоростями движения источника колеба­ний и приемника относительно среды, в которой происходит распространение звуко­вых волн. Эффект Доплера наблюдается также и при движении относительно друг друга источника и приемника электромагнитных волн. Таккак особой среды, служащей носителем электромагнитных волн, не существует, то частота световых волн, вос­принимаемых приемником (наблюдателем), определяется только относительной ско­ростью источника и приемника (наблюдателя). Закономерности эффекта Доплера для электромагнитных волн устанавливаются на основе специальной теории относитель­ности.

Согласно принципу относительности Эйнштейна (см. § 35), уравнение световой волны во всех инерциальных системах отсчета одинаково по форме. Используя преоб­разования Лоренца (см. § 36), можно получить уравнение волны, посылаемой источни­ком, в направлении приемника в другой инерциальной системе отсчета, а следователь­но, и связать частоты световых воли, излучаемых источником (n₀) и воспринимаемых приемником (n). Теория относительности приводит к следующей формуле, описыва­ющейэффект Доплера для электромагнитных волн в вакууме:

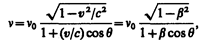(188.1)

где v — скорость источника света относительно приемника, с — скорость света в ваку­уме, b=v/c, q — угол между вектором скорости v и направлением наблюдения, из­меряемый в системе отсчета, связанной с наблюдателем. Из выражения (188.1) следует, что при q = 0

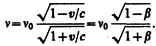(188.2)

Формула (188.2) определяет так называемый продольный эффект Доплера, наблюда­емый при движении приемника вдоль линии, соединяющей его с источником. При малых относительных скоростях v (v<<c), разлагая (188.2) в ряд по степеням b и пpeнeбрегая членом порядка b², получим

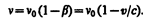(188.3)

Следовательно, при удалении источника и приемника друг от друга (при их положительной относительной скорости) наблюдается сдвиг в более длинноволновую область (n<n₀, l>l₀) — так называемоекрасное смещение. При сближении же ис­точника и приемника (при их отрицательной относительной скорости) наблюдается сдвиг в более коротковолновую область ((n>n₀, l<l₀) — так называемоефиолетовое смещение.

Если q=p/2, то выражение (188.1) примет вид

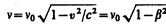(188.4)

Формула (188.4) определяет так называемый поперечный эффект Доплера, наблю­даемый при движении приемника перпендикулярно линии, соединяющей его с источником.

Из выражения (188.4) следует, что поперечный эффект Доплера зависит от b², т.е. при малых b является эффектом второго порядка малости по сравнению с продольным эффектом, зависящим от b (см. (188.3)). Поэтому обнаружение поперечного эффекта Доплера связано с большими трудностями. Поперечный эффект, хотя и много меньше продольного, имеет принципиальное значение, так как не наблюдается в акустике (при v<<с из (188.4) следует, что n = n₀!), и является, следовательно, релятивистским эффек­том. Он связан с замедлением течения времени движущегося наблюдателя. Экс­периментальное обнаружение поперечного эффекта Доплера явилось еще одним под­тверждением справедливости теории относительности; он был обнаружен в 1938 г. в опытах американского физика Г. Айвса.

Продольный эффект Доплера был впервые обнаружен в 1900 г. в лабораторных условиях русским астрофизиком А. А. Белопольским (1854—1934) и повторен в 1907 г. русским физиком Б. Б. Голицыным (1862—1919). Продольный эффект Доплера ис­пользуется при исследовании атомов, молекул, а также космических тел, так как по смещению частоты световых колебаний, которое проявляется в виде смещения или уширения спектральных линий, определяется характер движения излучающих частиц или излучающих тел. Эффект Доплера получил широкое распространение в радиотех­нике и радиолокации, например в радиолокационных измерениях расстояний до движу­щихся объектов.

§ 189. Излучение Вавилова — Черенкова

Российский физик П. А. Черенков (1904—1990), работавший под руководством Вави­лова, показал, что при движении релятивистских заряженных частиц в среде с постоян­ной скоростью v, превышающей фазовую скорость света в этой среде, т. е. при условии v>c/n (n—показатель преломления среды), возникает электромагнитное излучение, названное впоследствииизлучением (эффектом) Вавилова — Черенкова. Природа дан­ного излучения, обнаруженного для разнообразных веществ, в том числе и для чистых жидкостей, подробно изучалась С. И. Вавиловым. Он показал, что данное свечение не является люминесценцией (см. § 245), как считалось ранее, и высказал предположение, что оно связано с движением свободных электронов сквозь вещество.

Излучение Вавилова — Черенкова в 1937 г. было теоретически объяснено российс­кими учеными И. Е. Таммом (1895—1971) и И. М. Франком (р. 1908) (Черенков, Тамм и Франк в 1958 г. удостоены Нобелевской премии).

Согласно электромагнитной теории, заряженная частица (например, электрон) излучает электромагнитные волны лишь при движении с ускорением. Тамм и Франк показали, что это утверждение справедливо только до тех пор, пока скорость заряжен­ной частицы не превышает фазовой скорости с/n электромагнитных волн в среде, в которой частица движется. Если частица обладает скоростью v>c/n, то, даже двигаясь равномерно, она будет излучать электромагнитные волны. Таким образом, согласно теории Тамма и Франка, электрон, движущийся в прозрачной среде со скоростью, превышающей фазовую скорость света в данной среде, должен сам излу­чать свет.

Отличительной особенностью излучения Вавилова — Черенкова является его рас­пространение не по всем направлениям, а лишь по направлениям, составляющим острый угол q c траекторией частицы, т. е. вдоль образующих конуса, ось которого совпадает с направлением скорости частицы. Определим угол q:

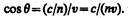(189.1)

Возникновение излучения Вавилова — Черенкова и его направленность истолкованы Франком и Таммом на основе представлений об интерференции света с использовани­ем принципа Гюйгенса.

На основе излучения Вавилова — Черенкова разработаны широко используемые экспериментальные методы для регистрация частиц высоких энергий и определения их свойств (направление движения, величина и знак заряда, энергия). Счетчики для регистрации заряженных частиц, в которых используется излучение Вавилова — Чере­нкова, получили название черенковских счетчиков. В этих счетчиках частица регист­рируется практически мгновенно (при движении заряженной частицы в среде со скоро­стью, превышающей фазовую скорость света в данной среде, возникает световая вспышка, преобразуемая с помощью фотоэлектронного умножителя (см. § 105) в им­пульс тока). Это позволило в 1955 г. итальянскому физику Э. Сегре (р. 1905) открыть в черенковском счетчике короткоживущую античастицу — антипротон.

Задачи

24.1. На грань стеклянной призмы (n =1,5) нормально падает луч света. Определить угол отклонения луча призмой, если ее преломляющий угол равен 25°. [14°21’]

24.2. При прохождении света в некотором веществе пути х его интенсивность уменьшилась в два раза. Определить, во сколько раз уменьшится интенсивность света при прохождении им пути 4х. [В 16 раз]

24.3. Источник монохроматического света с длиной волны l₀=0,6 мкм движется по направле­нию к наблюдателю со скоростью v=0,15 с (с — скорость света в вакууме). Определить длину волны l, которую зарегистрирует приемник. [516 нм]

24.4.Определить минимальную кинетическую энергию (в мегаэлектрон-вольтах), которой дол­жен обладать электрон, чтобы в среде с показателем преломления п =1,5 возникло излучение Вавилова — Черенкова. [0,17 МэВ]

Глава 25Поляризация света

§ 190. Естественный и поляризованный свет

Следствием теории Максвелла (см. § 162) является поперечность световых волн: векторы напряженностей электрического Е и магнитного Н полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (перпендикулярно лучу). Поэтому для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно светового вектора — вектора напряженности Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах вещества).

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равнове­роятными колебаниями светового вектора (рис. 272, а; луч перпендикулярен плоскости рисунка). В данном случае равномерное распределение векторов Е объясняется боль­шим числом атомарных излучателей, а равенство амплитудных значений векторов Е — одинаковой (в среднем) интенсивностью излучения каждого из атомов. Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) называется естественным.

Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление коле­баний вектора Е (рис. 272, б),то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу (рис. 272, в), называется плоскополяризованным (линейно поляризованным).

Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоско­стью поляризации. Плоскополяризованный свет является предельным случаем эллиптически поляризованного света — света, для которого вектор Е (вектор Н) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпен­дикулярной лучу. Если эллипс поляризации вырождается (см. § 145) в прямую (при разности фаз j, равной нулю или p), то имеем дело с рассмотренным выше плоскополяризованным светом, если в окружность (при j = ±p/2 и равенстве амплитуд склады­ваемых волн), то имеем дело с циркулярно поляризованным (поляризованным по кругу) светом.

Степенью поляризации называется величина

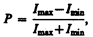
где I_max, и I_min — соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Для естественного света I_max=I_min и Р=0, для плоскополяризованного I_min =0 и Р=1.