Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 7 страница
где с — скорость распространения света в вакууме, v — скорость распространения света в среде. Так как n в среде всегда больше единицы, то, по теории Ньютона, v>c, т. е. скорость распространения света в среде должна быть всегда больше скорости его распространения в вакууме.
Согласно волновой теории, развитой на основе аналогии оптических и акустических явлений, свет представляет собой упругую волну, распространяющуюся в особой среде — эфире. Эфир заполняет все мировое пространство, пронизывает все тела и обладает механическими свойствами — упругостью и плотностью. Согласно Гюйгенсу, большая скорость распространения света обусловлена особыми свойствами эфира.
Волновая теория основывается на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих воли дает положение волнового фронта в следующий момент времени. Напомним, что волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t. Принцип Гюйгенса позволяет анализировать распространение света и вывести законы отражения и преломления.
Выведем законы отражения и преломления света, исходя из принципа Гюйгенса. Пусть на границу раздела двух сред падает плоская волна (фронт волны — плоскость AВ), распространяющаяся вдоль направления I (рис. 243). Когда фронт волны достигнет отражающей поверхности в точке A, эта точка начнет излучать вторичную волну. Для прохождения волной расстояния ВС требуется время Dt=BC/v. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен vDt=BC. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны — лучом II. Из равенства треугольников AВС и ADС вытекает закон отражения: угол отражения i’1, равен углу падения i1.
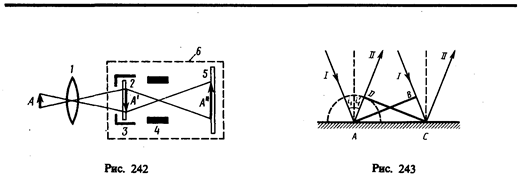
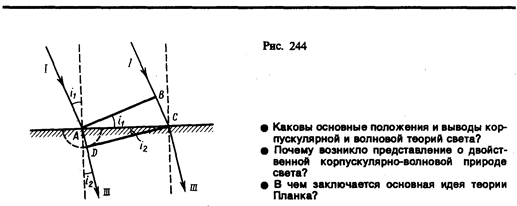
Для вывода закона преломления предположим, что плоская волна (фронт волны — плоскость AВ), распространяющаяся в вакууме вдоль направления I со скоростью света с, падает на границу раздела со средой, в которой скорость ее распространения равна v (рис. 244). Пусть время прохождения волной пути ВС равно Dt. Тогда BC=cDt. За это же время фронт волны, возбуждаемый точкой A в среде со скоростью v, достигнет точек полусферы, радиус которой AD=vDt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения — лучом III. Из рис. 244 следует, что AC=BC/sini1=AD/sini2, т. е. cDt/sini1=vDt/sini2c, откуда
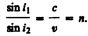 (170.2)
(170.2)
Сравнивая выражения (170.2) и (170.1), видим, что волновая теория приводит к выводу, отличному от вывода теории Ньютона. По теории Гюйгенса, v<c, т. е. скорость распространения света в среде должна быть всегда меньше скорости его распространения в вакууме.
Таким образом, к началу XVIII в. существовало два противоположных подхода к объяснению природы света: корпускулярная теория Ньютона и волновая теория Гюйгенса. Обе эти теории объясняли прямолинейное распространение света, законы отражения и преломления. XVIII век стал веком борьбы этих теорий. Экспериментальное доказательство справедливости волновой теории было получено в 1851 г., когда Э. Фуко (и независимо от него А. Физо) измерил скорость распространения света в воде и получил значение, соответствующее формуле (170.2). К началу XIX столетия корпускулярная теория была полностью отвергнута и восторжествовала волновая теория. Большая заслуга в этом отношении принадлежит английскому физику Т. Юнгу, исследовавшему явления дифракции и интерференции, и французскому физику О. Френелю (1788—1827), дополнившему принцип Гюйгенса и объяснившему эти явления.
Несмотря на признание волновой теории, она обладала целым рядом недостатков. Например, явления интерференции, дифракции и поляризации могли быть объяснены только в том случае, если световые волны считать поперечными. С другой стороны, если световые волны — поперечные, то их носитель — эфир — должен обладать свойствами твердых тел. Попытка же наделить эфир свойствами твердого тела успеха не имела, так как эфир не оказывает заметного воздействия на движущиеся в нем тела. Далее эксперименты показали, что скорость распространения света в разных средах различна, поэтому эфир должен обладать в разных средах различными свойствами. Теория Гюйгенса не могла объяснить также физической природы наличия разных цветов.
Наука о свете накапливала экспериментальные данные, свидетельствующие о взаимосвязи световых, электрических и магнитных явлений, что позволило Максвеллу в 70-х годах прошлого столетия создать электромагнитную теорию света (см. § 139). Согласно электромагнитной теории Максвелла (см. (162.3)),
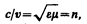
где с и v — соответственно скорости распространения света в вакууме и в среде с диэлектрической проницаемостью e и магнитной проницаемостью m. Это соотношение связывает оптические, электрические и магнитные постоянные вещества. По Максвеллу, e и m — величины, не зависящие от длины волны света, поэтому электромагнитная теория не могла объяснить явление дисперсии (зависимость показателя преломления от длины волны). Эта трудность была преодолена в конце XIXв. Лоренцем, предложившим электронную теорию, согласно которой диэлектрическая проницаемость e зависит от длины волны падающего света. Теория Лоренца ввела представление об электронах, колеблющихся внутри атома, и позволила объяснить явления испускания и поглощения света веществом.
Несмотря на огромные успехи электромагнитной теории Максвелла и электронной теории Лоренца, они были несколько противоречивы и при их применении встречался ряд затруднений. Обе теории основывались на гипотезе об эфире, только «упругий эфир» был заменен «эфиром электромагнитным» (теория Максвелла) или «неподвижным эфиром» (теория Лоренца). Теория Максвелла не смогла объяснить процессов испускания и поглощения света, фотоэлектрического эффекта, комптоновского рассеяния и т. д. Теория Лоренца, в свою очередь, не смогла объяснить многие явления, связанные с взаимодействием света с веществом, в частности вопрос о распределении энергии по длинам волн при тепловом излучении черного тела.
Перечисленные затруднения и противоречия были преодолены благодаря смелой гипотезе (1900) немецкого физика М. Планка (1858—1947), согласно которой излучение и поглощение света происходит не непрерывно, а дискретно, т. е. определенными порциями (квантами), энергия которых определяется частотой n:
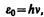 (170.3)
(170.3)
где h — постоянная Планка.
Теория Планка не нуждалась в понятии об эфире. Она объяснила тепловое излучение черного тела. Эйнштейн в 1905 г. создал квантовую теорию света, согласно которой не только излучение света, но и его распространение происходит в виде потока световых квантов — фотонов, энергия которых определяется соотношением (170.3), а масса
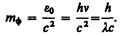 (170.4)
(170.4)
Квантовые представления о свете хорошо согласуются с законами излучения и поглощения света, законами взаимодействия света с веществом. Однако как с помощью этих представлений объяснить такие хорошо изученные явления, как интерференция, дифракция и поляризация света? Эти явления легко объясняются на основе волновых представлений. Все многообразие изученных свойств и законов распространения света, его взаимодействия с веществом показывает, что свет имеет сложную природу. Он представляет собой единство противоположных видов движения — корпускулярного (квантового) и волнового (электромагнитного). Длительный путь развития привел к современным представлениям о двойственной корпускулярно-волновой природе света. Выражения (170.3) и (170.4) связывают корпускулярные характеристики излучения — массу и энергию кванта — с волновыми — частотой колебаний и длиной волны. Таким образом, свет представляет собой единство дискретности и непрерывности.
§ 171. Когерентность и монохроматичность световых волн
Интерференцию света можно объяснить, рассматривая интерференцию волн (см. § 156). Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Taк как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек.
Понять физическую причину немонохроматичности, а следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время (t » 10–8с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени 10–8с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом.
Описанная модель испускания света справедлива и для любого макроскопического источника, так как атомы светящегося тела излучают свет также независимо друг от друга. Это означает, что начальные фазы соответствующих им волновых цугов не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы разных цугов отличаются для двух последующих актов излучения. Следовательно, свет, испускаемый макроскопическим источником, некогерентен.
Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга tког называетсявременем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. tког < t. Прибор обнаружит четкую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн.
Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние lког =сtког, называемое длиной когерентности (илидлиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.
Чем ближе волна к монохроматической, тем меньше ширина Dw спектра ее частот и, как можно показать, больше ее время когерентности tког, а следовательно, и длина когерентности lког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временнóй когерентностью.
Наряду с временнóй когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называютсяпространственно-когерентными. Радиусом когерентности(илидлиной пространственной когерентности) называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Таким образом, пространственная когерентность определяется радиусом когерентности. Радиус когерентности
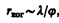
где l — длина волны света, j — угловой размер источника. Так, минимально возможный радиус когерентности для солнечных лучей (при угловом размере Солнца на Земле j » 10–2 рад и l » 0,5 мкм) составляет » 0,05 мм. При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза на расстоянии наилучшего зрения составляет лишь 0,1 мм. Отметим, что первое наблюдение интерференции провел в 1802 г. Т. Юнг именно с солнечным светом, для чего он предварительно пропускал солнечные лучи через очень малое отверстие в непрозрачном экране (при этом на несколько порядков уменьшался угловой размер источника света и тем самым резко увеличивался радиус когерентности (или длина пространственной когерентности)).
§ 172. Интерференция света
Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления: х1=А1 cos(w t + j1) и x2 = A2 cos(w t + j2). Под х понимают напряженность электрического Е или магнитного Н полей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях (см. § 162). Напряженности электрического и магнитного полей подчиняются принципу суперпозиции (см. § 80 и 110). Амплитуда результирующего колебания в данной точке  (см. 144.2)). Так как волны когерентны, то cos(j2 — j1) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (I ~ А2)
(см. 144.2)). Так как волны когерентны, то cos(j2 — j1) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (I ~ А2)
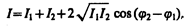 (172.1)
(172.1)
В точках пространства, где cos(j2—j1)>0, интенсивность I>I1+I2, где cos(j2—j1)<0, интенсивность I<I1+I2. Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Это явление называется интерференцией света.
Для некогерентных волн разность j2—j1 непрерывно изменяется, поэтому среднее во времени значение cos(j2—j1) равно нулю, и интенсивность результирующей волны всюду одинакова и при I1=I2 равна 2I1 (для когерентных волн при данном условии в максимумах I=4I1, в минимумах I=0).
Как можно создать условия, необходимые для возникновения интерференции световых волн? Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.
Пусть разделение на две когерентные волны происходит в определенной точке О. До точки M, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления п1 прошла путь s1, вторая — в среде с показателем преломления n2 — путь s2. Если в точке О фаза колебаний равна wt, то в точке М первая волна возбудит колебание A1cos(t–s1/v1), вторая волна — колебание A2cos(t–s2/v2), где v1=c/n1, v2=c/n2 — соответственно фазовая скорость первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна
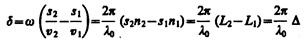
(учли, что w /с = 2pn/с = 2p/l0, где l0 — длина волны в вакууме). Произведение геометрической длины s пути световой волны в данной среде на показатель n преломления этой среды называетсяоптической длиной пути L, a D = L2 – L1 — разность оптических длин проходимых волнами путей — называетсяоптической разностью хода.Если оптическая разность хода равна целому числу длин волн в вакууме
 (172.2)
(172.2)
то d = ±2тp, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, (172.2) является условием интерференционного максимума.
Если оптическая разность хода
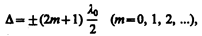 (172.3)
(172.3)
то d = ±2(т+1)p, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно, (172.3) является условием интерференционного минимума.
§ 173. Методы наблюдения интерференции света
Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров (см. § 233) во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.
1. Метод Юнга. Источником света служит ярко освещенная щель S (рис. 245), от которой световая волна падает на две узкие равноудаленные щели S1 и S2, параллельные щели S. Таким образом, щели S1 и S2 играют роль когерентных источников.
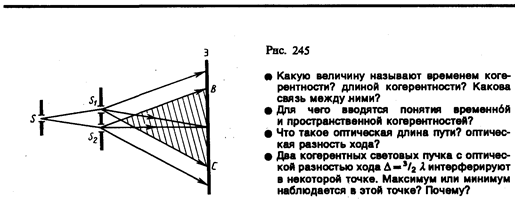
Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S1 и S2. Как уже указывалось (см. § 171), Т. Юнгу принадлежит первое наблюдение явления интерференции.
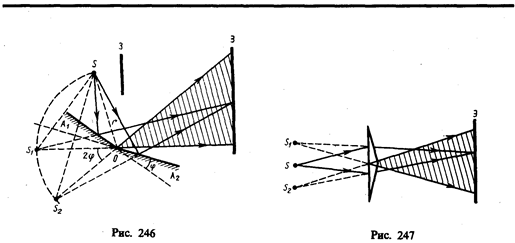
2. Зеркала Френеля. Свет от источника S (рис. 246) падает расходящимся пучком на два плоских зеркала А1О и А2О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол j мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S1 и S2 (угловое расстояние между которыми равно 2j) лежат на одной и той же окружности радиуса r с центром в О (точка соприкосновения зеркал).
Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S1 и S2, являющихся мнимыми изображениями S в зеркалах. Мнимые источники S1 и S2 взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2j. Интерференционная картина наблюдается на экране (Э), защищенном от прямого попадания света заслонкой (З).
3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 247) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S1 и S2, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.
Расчет интерференционной картины от двух источников. Расчет интерференционной картины для рассмотренных выше методов наблюдения интерференции света можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 248). Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей.
Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода D=s2—s1 (см. § 172). Из рис. 248 имеем
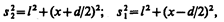
откуда 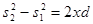 , или
, или

Из условия l >> d следует, что s1 + s2 » 2l, поэтому
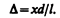 (173.1)
(173.1)
Подставив найденное значение D (173.1) в условия (172.2) и (172.3), получим, что максимумы интенсивности будут наблюдаться в случае, если
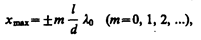 (173.2)
(173.2)
а минимумы — в случае, если
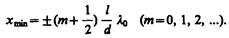 (173.3)
(173.3)
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно
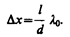 (173.4)
(173.4)
Dx не зависит от порядка интерференции (величины т) и является постоянной для данных l, d и l0. Согласно формуле (173.4), Dx обратно пропорционально d; следовательно, при большом расстоянии между источниками, например при d»l, отдельные полосы становятся неразличимыми. Для видимого света l0»10–7 м, поэтому четкая, доступная для визуального наблюдения интерференционная картина имеет место при l>>d (это условие и принималось при расчете). По измеренным значениям l, d и Dх, используя (173.4), можно экспериментально определить длину волны света. Из выражений (173.2) и (173.3) следует, таким образом, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий т=0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (т= 1), второго (т =2) порядков и т.д.
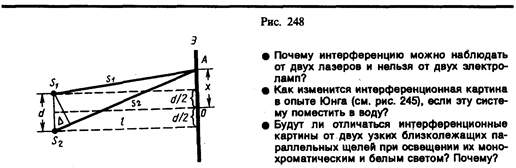
Описанная картина, однако, справедлива лишь при освещении монохроматическим светом (l0=const). Если использовать белый свет, представляющий собой непрерывный набор длин воли от 0,39мкм (фиолетовая граница спектра) до 0,75мкм (красная граница спектра), то интерференционные максимумы для каждой длины волны будут, согласно формуле (173.4), смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин воли совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т. д. (ближе к белой полосе будут находиться зоны фиолетового цвета, дальше — зоны красного цвета).
§ 174. Интерференция света в тонких пленках
В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленка на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки.
Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i (рис. 249) падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (п0=1), а частично отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В результате возникает интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами.
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ,
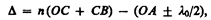
где показатель преломления окружающей пленку среды принят равным 1, а член ± l0/2 обусловлен потерей полуволны при отражении света от границы раздела. Если п>n0, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус; если же п<n0, то потеря полуволны произойдет в точке С и l0/2 будет иметь знак плюс. Согласно рис. 249, OC=CB=d/cosr, OA = OB sin i = 2d tg r sin i. Учитывая для данного случая закон преломления sin i = n sin r, получим
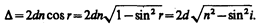
С учетом потери полуволны для оптической разности хода получим
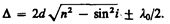 (174.1)
(174.1)
Для случая, изображенного на рис. 249 (п>n0),
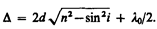
В точке Р будет интерференционный максимум, если (см. (172.2))
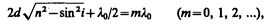 (174.2)
(174.2)
и минимум, если (см. (172.3))
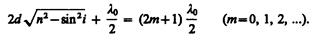 (174.3)
(174.3)
Интерференция, как известно, наблюдается, только если удвоенная толщина пластинки меньше длины когерентности падающей волны.
Полосы равного наклона (интерференция от плоскопараллельной пластинки). Из выражений (174.2) и (174.3) следует, что интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами l0, d, п и i. Для данных l0, d, и n каждому наклону i лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называютсяполосами равного наклона.
Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки (рис. 250), параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1' и 1" «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. 250 ее оптическая ось параллельна лучам 1' и 1"), в эту же точку придут и другие лучи (на рис. 250 – луч 2), параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
Дата добавления: 2017-04-20; просмотров: 453;
