Уравнения (34.1) и (34.2) носят название преобразовавши координат Галилея.
В частном случае, когда система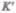 
движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат 
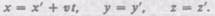Галилея имеют вид
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:
(34.3)
Записанные соотношения справедливы лишь в случае классической механики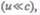 
А при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются
более общими преобразованиями Лоренца* (§ 36).
Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение
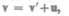(34.4)
которое представляет собой правило сложения скоростей в классической механике. Ускорение в системе отсчета К
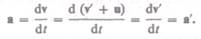
Таким образом, ускорение точки А в системах отсчета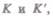 
движущихся друг
относительно друга равномерно и прямолинейно, одинаково:
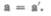(34.5)
Следовательно, если на точку А другие тела не действуют (а=0), то, согласно (34.5), и 
т. е. система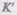 
является инерциальной (точка движется относительно нее
Дата добавления: 2017-04-20; просмотров: 415;