Статистических характеристик

Применение выборочного метода может базироваться на отборе из генеральной совокупности теоретически любого числа статистических единиц. Математически доказано, что выборочные совокупности могут быть малые и большие. Если выборка насчитывает не более 30 единиц, то она называется малой, свыше 30 единиц – большой.

Вероятностная оценка результатов малой выборки отличается от оценки в большой выборке тем, что при малом числе наблюдений распределение вероятностей, например, для средней в большей степени зависит от числа отобранных единиц. Английский статистик Вильям Госсет (псевдоним "Стьюдент") изучил распределение отклонения выборочных средних от генеральной или стохастической средней и доказал, что оценка расхождения между выборочной средней малой выборки и генеральной средней имеет особый закон распределения. Распределение Стьюдента названо законом малых выборок. Доказано, что при численности выборки более 30 единиц вариационный ряд дает нормальное распределение вероятностей.

Основные статистические характеристики (средняя, дисперсия, коэффициент вариации и дp.) для малых выборок приходится корректировать через коэффициент 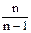, т.е. применять точечную оценку этих характеристик. Обычно она выражается каким-то одним числом. Это означает, что для малой выборки рассчитанные выборочные средние, дисперсии, средние квадратические отклонения, коэффициенты вариации и т. д. необходимо умножить на 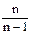Только при этом условии любая статистическая характеристика может считаться несмещенной (состоятельной, действительной).

Нескорректированные статистические характеристики, рассчитанные по данным малой выборки, обычно считаются смещенными (несостоятельными, недействительными) , так как они могут иметь существенные расхождения с аналогичными характеристиками генеральной совокупности и, следовательно, не могvт быть репрезентативны.

Значит, для получения точечной состоятельной оценки по данным малой выборки необходимо найти скорректированные статистические характеристики. Так, среднее значение признака в генеральной совокупности теоретически может быть рассчитано следующим образом:

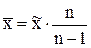(8.10)

где 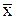– среднее значение признака в генеральной совокупности; 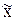– среднее значение признака в выборочной совокупности; n – численность выборки.

Если из генеральной совокупности выбрана только одна статистическая единица, то совершенно очевидно, что ее статистические характеристики не могут быть репрезентативными по отношению к генеральной совокупности. Этому можно найти довольно простое доказательство:

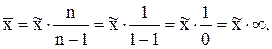
Результат показывает, что если оценивать среднее значение признака в генеральной совокупности по значению признака, полученному на основе отбора только одной статистической единицы, то ожидаемое среднее значение теоретически может выражаться бесконечной величиной.

При условии отбора двух статистических единиц среднее значение по генеральной и выборочной совокупностям может различаться в два раза 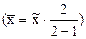; при трех единицах – в 1,5 раза. Совершенно очевидно, что точечная оценка среднего значения признака в генеральной совокупности в приведенных примерах не может считаться состоятельной.

Другое дело, когда численность выборки составляет не менее 30 статистических единиц. В этом случае для получения точечной характеристики в генеральной совокупности поправочной коэффициент 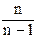практически приближается к единице. И поэтому статистические характеристики, полученные на основе больших выборок, оцениваются как несмещенные (состоятельные, действительные). Это означает, что такие выборочные характеристики могут считаться представительными для генеральной статистической совокупности. Например, выборочное наблюдение по 30 крестьянским хозяйствам показало, что яйценоскость кур-несушек составляет 300 яиц в год. Для нахождения точечной оценки средней яйценоскости кур-несушек во всех крестьянских хозяйствах можно воспользоваться формулой (8.10):

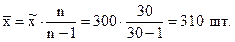
Следовательно, если применить прием точечной оценки годовой яйценоскости кур-несушек на основе выборочного метода, то можно утверждать, что средняя яйценоскость в генерльной совокупности будет составлять 310 яиц в год.