Статистических характеристик

Предельная ошибка выборки представляет собой расхождение между статистическими характеристиками, полученными в выборочной и генеральной совокупностях. Как было показано выше (формула 6.2), предельная погрешность может накапливаться только за счет неполного охвата статистических единиц генеральной совокупности при проведении выборочного наблюдения. Именно поэтому статистические характеристики, полученные в результате выборочного наблюдения, могут не совпадать с аналогичными характеристиками в генеральной совокупности.

Предельная ошибка выборки зависит непосредственно от выборочной средней ошибки и доверительного коэффициента. Поскольку вопрос о средней ошибке выборки уже рассмотрен, то попытаемся представить себе предельную погрешность, неизбежно допускаемую при проведении выборочного наблюдения, т.е.

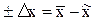, (8.11)

где Δх – предельная ошибка выборки; 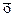– среднее значение признака в генеральной совокупности; 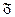– среднее значение признака в выборочной совокупности.

Нахождение предельной ошибки выборки по данным выборочного наблюдения позволяет определить границы, в которых заключены значения статистических характеристик, принадлежащих генеральной статистической совокупности. С этой целью используется интервальная оценка выборочных статистических характеристик. Например, интервальную оценку выборочного среднего значения теоретически можно получить из формулы (8.1), преобразовав ее следующим образом:

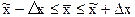. (8.12)

Это означает, что среднее значение признака в генеральной совокупности заключено в границах, нижняя величина которой представляет собой разность между средней выборочной и предельной ошибкой выборки, а верхняя – сумму этих значений.

Допустим, необходимо найти интервальную оценку при 5 % уровне значимости (95 % уровня вероятности) среднего выхода меда на одну пчелосемью по всей пчелопасеке (100 семей), если известно, что выборочным обследованием охвачено 25 пчелосемей; при этом средний выход меда составил 25 кг, а среднее квадратическое отклонение – 10 кг на одну пчелосемью.

Решение проводим по формуле (8.12). Поскольку выборочный средний выход меда на одну пчелосемью по условию задачи составляет 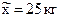, то для нахождения интервальной оценки необходимо рассчитать предельную ошибку выборки Δх, которую определяем по формуле (6.2), т.е. 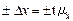. В свою очередь доверительный коэффициент t, который соответствует вероятности 0,95, находим по специальной таблице (приложение I). Он равен 1,96. Cpeднюю ошибку выборки ( 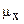.) рассчитываем по формуле (8.4):

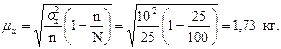
Следовательно, предельная ошибка выборки составит:

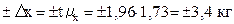меда на одну пчелосемью.

Таким образом, интервальную оценку генеральной средней массы меда на одну семью по всей пчелопасеке можно записать так:

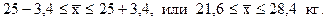
Это означает, что средний выход мела на одну пчелосемью по всей пасеке находится в пределах от 21,6 до 28,4 кг.