Средняя геометрическая величина
Если в формулу 6.1 подставить значение К=0, то в результате получаем среднюю геометрическую величину, которая имеет простую (невзвешенную) и взвешенную формы.
Средняя геометрическая простая величина, рассчитываемая в ранжированном ряду, выражается следующим образом:
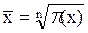 (6.8)
(6.8)
где 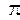 – знак произведения; х – варианты; n – общее число вариант в ранжированном ряду.
– знак произведения; х – варианты; n – общее число вариант в ранжированном ряду.
Для дискретного или интервального ряда средняя геометрическая рассчитывается по взвешенной форме:
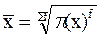 (6.9)
(6.9)
где f – частота дискретного или интервального ряда.
Средняя геометрическая величина применяется в тех случаях, когда варианты связаны между собой знаком произведения, т.е. главным образом при расчёте относительных показателей динамики: средних коэффициентов (темпов) роста, прироста и др.
Например, необходимо рассчитать, во сколько раз в среднем возросло производство сахарной свеклы в сельскохозяйственной организации за четырёхлетие, если известно, что цепные коэффициенты роста по годам составляли соответственно 1; 0,9; 1,3; 1,5 раза. При решении этой задачи рассуждаем так: цепные коэффициенты роста не автономны, как в вариационном ряду распределения, а взаимозависимы, т.е. связаны между собой знаком произведения. Следовательно, наиболее точный результат может быть получен при условии применения средней геометрической невзвешенной величины по формуле (6.8):
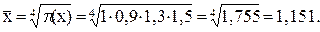
Таким образом, производство сахарной свеклы в приведенном четырехлетии за каждый год в среднем возрастало в 1,151 раза.
Если есть дискретный или интервальный ряд, то при расчёте средней целесообразно воспользоваться взвешенной формой средней геометрической величины. Допустим, необходимо рассчитать среднегодовой темп роста валового производства картофеля в районе за 20-ти летний период по данным табл. 6.7.
Т а б л и ц а 6.7. Динамика валового производства картофеля в районе
| Темпы роста производства картофеля, % | Число лет в каждом периоде | |
| Интервалы | Середина интервала | |
| х | f | |
| 90-100 | ||
| 100-110 | ||
| 110-120 | ||
| 120-130 | ||
| Σ | - |
Как видно, темпы роста производства картофеля представлены в виде интервального ряда, а они связаны между собой знаком не суммы, а произведения. Это означает, что для расчёта среднего темпа роста за весь 20-ти летний период целесообразно применить взвешенную форму средней геометрической величины (формула 6.9):
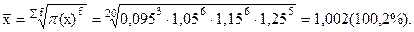
Таким образом, за двадцатилетний период производство картофеля развивалось со среднегодовым темпом роста 100,2 %.
Дата добавления: 2017-04-20; просмотров: 682;
