Оценка качества модели множественной регрессии

Проверка качества модели множественной регрессии может быть осуществлена с помощью дисперсионного анализа.

Как уже было отмечено (см. 2.5), сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений 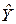, полученных по уравнению регрессии, от выборочного среднего 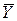плюс сумма квадратов отклонений Y от линии регрессии .

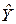С учетом (3.21) получим таблицу дисперсионного анализа (табл. 3.4), аналог таблицы 2.3.

Проверка качества модели множественной регрессии в целом может быть осуществлена с помощью F-критерия Фишера. Для проверки гипотезы о том, что линейная связь между 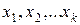и y отсутствует:

,

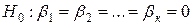воспользуемся соотношением

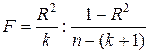(3.23)

которое удовлетворяет F - распределению Фишера с (k, n-(k+1)) степенями свободы. Критические значения этой статистики F_e для уровня значимости e затабулированы.

Таблица 3.4

Таблица дисперсионного анализа

Источник вариации	Сумма квадратов отклонений	Число степеней свободы	Дисперсия на одну степень свободы
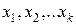
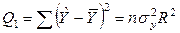
		k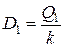
Остаток		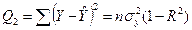n-k-1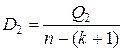
Общая вариация		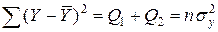n-1

Если F>F_e, то гипотеза об отсутствии связи между переменными 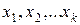и y отклоняется, в противном случае гипотеза Н₀ принимается и уравнение регрессии не значимо.

Пример (продолжение примера 1). Заполним таблицу дисперсионного анализа:

Таблица дисперсионного анализа

Источник вариации	Сумма квадратов отклонений	Число степеней свободы	Дисперсия
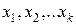
	5828,84		2914,42
Остаток	2049,54		120,56
Общая вариация	7878,38

Получаем , .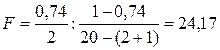

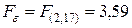В нашем примере F>F_e, следовательно, нулевая гипотеза отклоняется, и уравнение множественной регрессии значимо. Ñ

Помимо проверки значимости уравнения в целом, можно проверить статистическую значимость каждого из коэффициентов регрессии в отдельности.

Фактически это означает проверку одной из гипотез:

1) 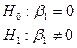; …; k) .

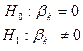Статистическая значимость каждого из коэффициентов регрессии определяется при помощи t-критерия Стьюдента. Решение о том, что верна нулевая гипотеза, принимается в случае, когда |t|<t_e, иначе принимается альтернативная гипотеза.

Значение t-статистики Стьюдента в случае множественной регрессии определяется по формуле:

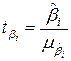, (3.24)

где 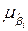- стандартная ошибка коэффициента регрессии 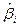, которая определяется по формуле

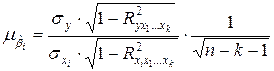, (3.25)

здесь 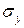- стандартное отклонение y;

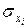- стандартное отклонение x_i;

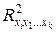- коэффициент детерминации для зависимости фактора x_i от других факторов уравнения множественной регрессии.

Пример (продолжение примера 1). Проверим значимость коэффициентов регрессии. В случае, когда в уравнение регрессии включены две независимые переменные, формула (3.24) упрощается

, .

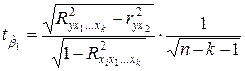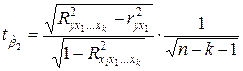Таким образом:

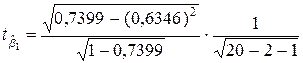=4,69, 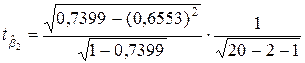=4,50,

.

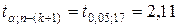Так как в обоих случаях , то коэффициенты регрессии значимы, следовательно, и вес груза, и расстояние грузовой перевозки оказывают существенное, статистически значимое влияние на стоимость перевозки. Ñ