Сопоставление коэффициентов значимости функций и их стоимости
| Ранг функции | Значимость, % | Удельный вес затрат на функцию в общих затратах, % | К затрат на функцию |
| 1,00 1,67 0,33 0,30 0,40 | |||
| Итого | --- |
Сопоставив удельный вес затрат на функцию в общих затратах и значимость соответствующей ему функции можно вычислить коэффициент затрат по функциям (гр. 4, табл. 13).
Оптимальным считается Кз/ф » 1. Кз/ф 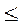 1 желательнее, чем Кз/ф
1 желательнее, чем Кз/ф 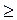 1. При существенном превышении данного коэффициента единицы необходимо искать пути удешевления данной функции. В нашем примере (табл. 13) такой является функция с 30% -м, вторым, уровнем значимости.
1. При существенном превышении данного коэффициента единицы необходимо искать пути удешевления данной функции. В нашем примере (табл. 13) такой является функция с 30% -м, вторым, уровнем значимости.
Результатом проведенного ФСА являются варианты решения, в которых необходимо сопоставить совокупные затраты на изделия, являющиеся суммой поэлементных затрат, с какой-либо базой. Этой базой могут служить минимально возможные затраты на изделие. Теория ФСА предлагает исчислять экономическую эффективность, которая показывает, какую долю составляет снижение затрат в их минимально возможной величине.
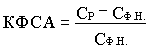 , (5.2)
, (5.2)
где
КФСА – экономическая эффективность ФСА (коэффициент снижения текущих затрат);
СР – реально сложившиеся совокупные затраты;
СФ.Н. – минимально возможные затраты, соответствующие спроектированному изделию.
4. Исследовательский этап – оцениваются предлагаемые варианты разработанного изделия.
5. Рекомендательный этап – отбираются наиболее приемлемые для данного производства варианты разработки и усовершенствования изделия.
С этой целью можно рекомендовать построение матричной таблицы (табл. 14).
Таблица 14.
Таблица решений по вариантам выбора изделий для производства
| 
| А Значимость функции: высокая Затраты: низкие Рентабельность изделия: высокая | В Значимость функции: высокая Затраты: средние Рентабельность изделия: средняя | С Значимость функции: высокая Затраты: высокие Рентабельность изделия: средняя |
| 
| D Значимость функции: средняя Затраты: низкие Рентабельность изделия: высокая | E Значимость функции: средняя Затраты: средние Рентабельность изделия: средняя | F Значимость функции: средняя Затраты: высокие Рентабельность изделия: низкая (средняя?) |
| 
| G Значимость функции: низкая Затраты: низкие Рентабельность изделия: средняя | H Значимость функции: низкая Затраты: средние Рентабельность изделия: низкая | I Значимость функции: низкая Затраты: высокие Рентабельность изделия: низкая |
С учетом значимости функций изделия, его узлов, деталей и уровня затрат посредством ценообразования, основываясь на знании спроса на продукцию определяется уровень ее рентабельности. Все это в совокупности служит цели принятия решения о выборе конкретного изделия к производству или направлений и масштаба его усовершенствования.
Существенную помощь в определении затрат на качество продукции могут оказать методы технического нормирования. Они основаны на расчете норм и нормативов материальных ресурсов (сырья, покупных комплектующих изделий и др.), расчете трудоемкости и иных затрат, включаемых в себестоимость продукции в соответствии с проектными размерами, конкретной технологией ее изготовления, хранения и транспортировки, а также затрат на гарантийное и сервисное обслуживание. Методы технического нормирования позволяют достаточно точно определить затраты как на новое изделие и при усовершенствовании продукции по его составляющим.
Если предприятие переходит к производству новой продукции, имевшей ранее аналог по потребительскому назначению и свойствам, то затраты на качество (ЗК) будут определяться разностью между затратами на старую (ЗСТ) и новую (ЗН) продукцию:
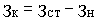 . (5.3)
. (5.3)
Если предприятие усовершенствует качественные параметры производимого ранее изделия, то затраты на качество можно определить прямым счетом по соответствующим норам и направлениям.
Степень тесноты связи между какими-либо характеристиками качества, имеющими количественное выражение, и затратами на него или ценой изделия, как формой его стоимости, в которой основной удельный вес занимают затраты, позволяет определить коэффициент корреляции.
Коэффициент корреляции может принимать значения от -1 до +1, т. е.
-1 < r < 1
При r близком к |1| можно говорить о высокой степени тесноты связи между исследуемыми переменными и напротив: при r близком к 0 корреляция между ними выражена слабо. Если r=|1|, все точки на диаграмме рассеивания будут лежать на прямой. Такая зависимость называется функциональной, когда r = 0, корреляционная связь между факторным и результативным показателями отсутствует. Знак «+» или «-» говорит о направлении связи – прямом или обратном.
Например, значение r, равное +0,758, свидетельствует о наличии высокой положительной корреляции между упаковкой товара, являющейся одним из показателей его качества и ценой на него, в которой воплощены затраты на товар.
Одним из методов, позволяющих проанализировать изменение затрат, связанных с изменением качества продукции является индексный метод. Сложность его применения к данному предмету исследования заключается в том, что оба признака должны быть выражены количественно. Качество же, не всегда имеет количественное значение и может описываться словесно, например: продукция пригодная и не прошедшая сертификацию, соответствующая и не соответствующая техническим условиям и др.
Если показатели качество имеют числовые характеристики, при построении индексов их можно использовать как весы затрат. В противном случае весами может служить количество элементов конструкции изделия, количество деталей, узлов, изделий.
В табл. 15 приведены данные о запланированной и фактической стоимости стального листа, используемого для производства труб, турбин и т.д.
Таблица 15.
Дата добавления: 2017-04-20; просмотров: 834;
