Дифференцирование функций комплексного переменного. Аналитические функции
Пусть функция  определена в некоторой области
определена в некоторой области 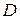 комплексного переменного
комплексного переменного 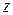 . Пусть точки
. Пусть точки 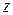 и
и 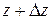 принадлежат области
принадлежат области 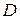 . Обозначим:
. Обозначим:

Определение.Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 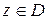 , если отношение
, если отношение  имеет конечный предел при
имеет конечный предел при 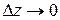 произвольным образом. Этот предел называется производной функции
произвольным образом. Этот предел называется производной функции  и обозначается символом
и обозначается символом 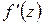 (или
(или 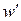 , или
, или 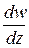 ), так что по определению
), так что по определению
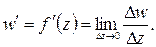
Если 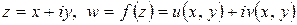 , то в каждой точке дифференцируемости функции
, то в каждой точке дифференцируемости функции  выполняются соотношения:
выполняются соотношения:

называемые условиями Коши-Римана.
Обратно, если в некоторой точке 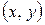 функции
функции 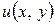 и
и 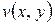 дифференцируемы как функции действительных переменных
дифференцируемы как функции действительных переменных 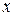 и
и  и, кроме того, удовлетворяют условиям Коши-Римана, то функция
и, кроме того, удовлетворяют условиям Коши-Римана, то функция  является дифференцируемой в точке
является дифференцируемой в точке 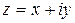 как функция комплексного переменного
как функция комплексного переменного 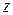 .
.
Определение.Функция  называется аналитической в данной точке
называется аналитической в данной точке 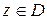 , если она дифференцируема как в самой точке
, если она дифференцируема как в самой точке 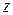 , так и в некоторой её окрестности. Функция
, так и в некоторой её окрестности. Функция  называется аналитической в области
называется аналитической в области  , если она дифференцируема в каждой точке этой области.
, если она дифференцируема в каждой точке этой области.
Для любой аналитической функции  имеем:
имеем:
 .
.
Пример 8.Показать, что функция  является аналитической на всей комплексной плоскости.
является аналитической на всей комплексной плоскости.
Решение. Имеем: 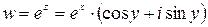 , так что
, так что
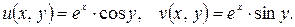
Для функций 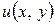 и
и 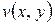 проверим выполнение условий Коши-Римана:
проверим выполнение условий Коши-Римана:
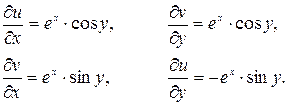
Условия Коши-Римана выполняются во всех точках. Значит, функция  всюду аналитическая. Тогда
всюду аналитическая. Тогда
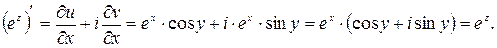
Итак, 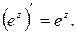
Пример 9.Является ли функция 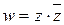 аналитической хотя бы в одной точке?
аналитической хотя бы в одной точке?
Решение.Имеем:  , так что
, так что
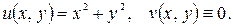
Найдём частные производные функций 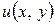 и
и 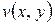 :
:
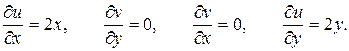
Условия Коши-Римана в этом случае имеют вид:
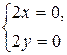
и удовлетворяются только в одной точке 
Следовательно, функция 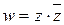 дифференцируема только в точке
дифференцируема только в точке 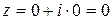 и нигде не аналитична.
и нигде не аналитична.
Таким образом,
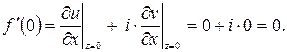
Для производных от функций комплексного переменного имеют место правила, аналогичные соответствующим правилам для производных от функций действительного переменного. А именно: если в точке 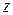 существуют производные
существуют производные 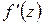 и
и 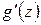 , то существуют и производные
, то существуют и производные 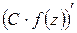 ,
, 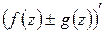 ,
, 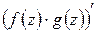 ,
, 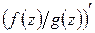 , причём выполняются следующие равенства:
, причём выполняются следующие равенства:
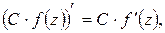 где
где 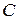 – комплексное число;
– комплексное число;
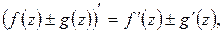
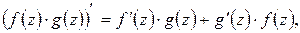
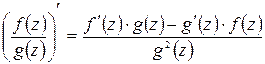 (при
(при 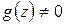 ).
).
Производные основных элементарных функций находятся по тем же формулам, что и для действительного аргумента:
1. 
| 7. 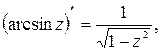
|
2. 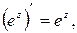
| 8. 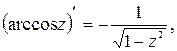
|
3. 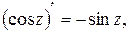
| 9. 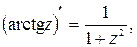
|
4. 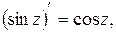
| 10. 
|
5. 
| 11. 
|
6. 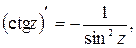
| 12. 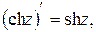
|
7. 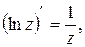
| 13. 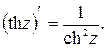
|
Если функция  – аналитическая в области
– аналитическая в области 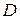 , то её действительная часть
, то её действительная часть 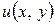 и мнимая часть
и мнимая часть 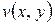 являются функциями, гармоническими в области
являются функциями, гармоническими в области 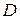 . Это значит, что у каждой из функций
. Это значит, что у каждой из функций 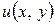 и
и 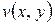 существуют непрерывные в
существуют непрерывные в 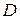 частные производные 2-го порядка, и для каждой из них верно уравнение Лапласа:
частные производные 2-го порядка, и для каждой из них верно уравнение Лапласа:
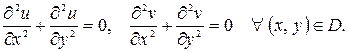
Если функция 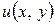 (функция
(функция 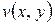 ) является гармонической в некоторой области
) является гармонической в некоторой области 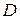 (вообще говоря, односвязной, т.е. ограниченной замкнутой несамопересекающейся линией), то существует аналитическая в
(вообще говоря, односвязной, т.е. ограниченной замкнутой несамопересекающейся линией), то существует аналитическая в 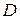 функция
функция  с действительной частью
с действительной частью 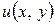 (соответственно, с мнимой частью
(соответственно, с мнимой частью 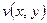 ), определяемая с точностью до постоянного слагаемого.
), определяемая с точностью до постоянного слагаемого.
Пользуясь условиями Коши-Римана, аналитическую функцию  можно восстановить, если известна её действительная часть
можно восстановить, если известна её действительная часть 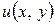 или мнимая часть
или мнимая часть 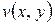 .
.
Пример 10.Восстановить функцию  по известной её действительной части
по известной её действительной части  и дополнительном условии
и дополнительном условии 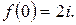
Решение.Проверим, является ли функция 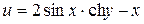 гармонической.
гармонической.
Имеем: 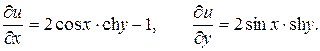 Вычислим частные производные 2-го порядка:
Вычислим частные производные 2-го порядка:
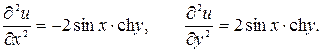
Отсюда 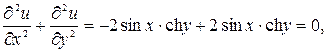 т.е. функция
т.е. функция 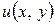 удовлетворяет уравнению Лапласа, а, значит, является гармонической.
удовлетворяет уравнению Лапласа, а, значит, является гармонической.
Имеем: 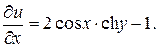 По первому из условий Коши-Римана должно быть
По первому из условий Коши-Римана должно быть 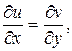 так что
так что 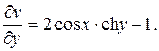
Отсюда  где функция
где функция 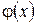 пока неизвестна.
пока неизвестна.
Дифференцируя 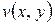 по
по 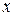 и используя второе из условий Коши-Римана, получим:
и используя второе из условий Коши-Римана, получим:
 а так как
а так как  то
то
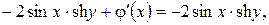 отсюда
отсюда 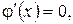 а значит
а значит 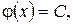 где
где 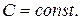
Итак,  и, следовательно,
и, следовательно,
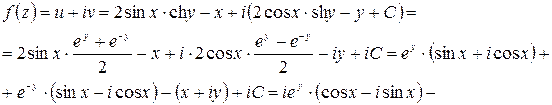
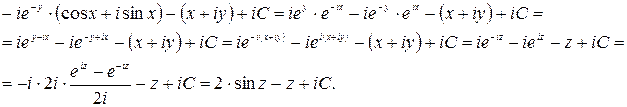
Таким образом, 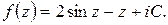 Постоянную
Постоянную 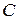 найдём из условия
найдём из условия  т.е.
т.е. 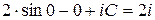 , отсюда
, отсюда 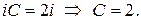
Ответ: 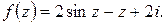
Дата добавления: 2017-04-20; просмотров: 4803;
