Основные виды рычажных механизмов

Основные виды рычажных механизмов.

1. Кривошипно-ползунный механизм.

а) центральный (рис.1);

б) внеосный (дезоксиальный) (рис.2);

е - эксцентриситет

Рис. 2

1-кривошип, т.к. звено совершает полный оборот вокруг своей оси;

2-шатун, не связан со стойкой, совершает плоское движение;

3-ползун (поршень), совершает поступательное движение;

4-стойка.

2. Четырехшарнирный механизм.

Звенья 1,3 могут быть кривошипами.

Если зв.1,3 – кривошипы, то механизм двукривошипный.

Если зв.1 – кривошип (совершает полный оборот), а зв.3 – коромысло (совершает неполный оборот), то механизм кривошипно-коромысловый.

Если зв.1,3 – коромысла, то механизм двукоромысловый.

3. Кулисный механизм.

1 - кривошип;

2 - камень кулисы (втулка) вместе с зв.1 совершает полный оборот вокруг А (w1 и w2 одно и тоже), а также движется вдоль зв.3, приводя его во вращение;

3 - коромысло (кулиса).

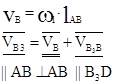на зв.3 выбирают точку В₃ и выбирают в данный момент так, чтобы она совпадала с точкой В.

4.Гидроцилиндр

(в кинематическом отношении подобен кулисному механизму).

В процессе проектирования конструктор решает две задачи:

· анализа (исследует готовый механизм);

· синтеза (проектируется новый механизм по требуемым параметрам);

Лекция 2.

Глава 1. Анализ рычажных механизмов.

В данной главе будут рассмотрены вопросы:

1. структурный анализ механизма (изучение строения механизма);

2. изучение классов и видов кинематических пар.

3. определение числа степеней свободы механизма и определение наличия или отсутствия избыточных связей; в случае наличия – дать рекомендации по способу их устранения;

4. кинематический анализ механизма.

§1.1

Примечание:

Кинематическая пара существует, если не происходит деформации звеньев, образующих эту пару, и не должно происходить отрыва звеньев одно от другого, образующих кинематическую пару.

Примечание:

Ограничения, накладываемые на независимые движения звеньев, образующих кинематическую пару, называются – условия связи S.

Число степеней свободы механизма

W=S+H,

где Н – подвижность.

Любое незакрепленное тело в пространстве имеет 6 степеней свободы, на плоскости – 3.

Классификация кинематических пар проводят либо числу связей, либо по числу подвижностей:

Число связей Класс КП Число подвижностей

S=1 P_I H=5

S=2 P_II H=4

S=3 P_III H=3

S=4 P_IVH=2

S=5 P_VH=1

Существует 5 классов кинематических пар.

Примеры различных КП смотри рис. 4-95.

Кинематические пары по характеру контакта звеньев, образующих КП, разделяют на:

1. низшие:

· вращательные;

· поступательные;

2. высшие.

Контакт звеньев в низшей КП осуществляется по поверхности. Контакт звеньев в высшей КП – либо по линии, либо в точке.

§1.2 Определение числа степеней свободы рычажных механизмов.

1.2.1 Плоские механизмы.

В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма.

ФОРМУЛА ЧЕБЫШЕВА: W_пп=3n -2p_н -p_в,

Где n – число подвижных звеньев механизма, р_н – число низших КП, р_в – число высших КП.

n=3

p_н=4

р_в=0

W=3^.3-2^.2=1

Рис.1.2.1

1.2.2 Пространственные механизмы.

В пространственном механизме оси непараллельны, звенья могут двигаться в разных плоскостях.

W_пр= 6n - (S₁+ S₂+ S₃+ S₄+ S₅)

Допустим, что механизм, изображенный на рис.1.2.1 – пространственный и все кинематические пары 5-го класса, т.е. одноподвижны A_V,B_V,C_V,D_V, тогда

W_пр= 6n - (5p_V+4p_IV+3p_III+2p_II+p_I)

W_пр= 6^.3 - 5^.4 = -2 à статически неопределимая ферма.

Для получения W_действ=0, необходимо добавить 3 движения.

q= W_действ - W_пр = 1 - (-2) = 3,

где q – избыточные связи.

Для того чтобы их устранить, надо изменить класс некоторых кинематических пар, при этом нельзя изменять класс КП А. Поэтому, сделаем КП В – сферическим шарниром, т.е. 3-го класса (добавим 2 подвижности), а КП С – 4-го класса (добавим 1 подвижность). Тогда

W_пр= 6^.3 - ( 5^.2 + 4^.1 + 3^.1 ) = 18 - 17 = 1

_n

ФОРМУЛА СОМОВА-МАЛЫШЕВА:W_пр= 6^.n - ΣS_i + q

ⁱ⁼¹

§1.3 Кинематический анализ рычажных механизмов.

1.3.1 Основные понятия и определения.

Зависимость линейных координат в какой-либо точке механизма от обобщенной координаты – линейная функция положения данной точки в проекциях на соответствующие оси координат.

Х_с= f(j₁)

Зависимость угловой координаты какого-либо звена механизма от обобщенной координаты – угловая функция положения данного звена.

j₂= f(j₁)

Первая производная линейной функции положения точки по обобщенной координате – линейная передаточная функция данной точки в проекциях на соответствующие оси координат (иногда называют «аналог линейной скорости…»)

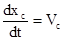
полная скорость т. С будет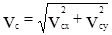

Первая производная угловой функции положения звена по обобщенной координате – передаточное отношение.

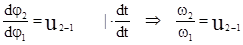
Вторая производная линейной функции положения по обобщенной координате – аналог линейного ускорения точки в проекциях на соответствующие оси.

Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена.

1.3.2 Аналитический способ определения кинематических параметров рычажных механизмов.

Дано: w₁, l_AB, l_BS2, l_BC, l_AC

Определить: v_i, a_i, w₂, e₂.

Для исследования плоских рычажных механизмов для решения данной задачи целесообразно использовать метод проецирования векторного контура на оси координат.

Для определения функции положения точки С представим длины звеньев в виде векторов.

Условие замкнутости данного контура:

(1)

(2)

(3)

рис.1.3.2 из (3) следует, что

(4)

Лекция 3.

Продифференцируем (3) по обобщенной координате:

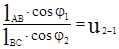(5)

Продифференцируем (2) по обобщенной координате:

Если необходимо определить функции положения центра масс, то вы делим векторный контур ABS₂

Условие замкнутости данного векторного контура имеет вид:

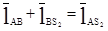(6)

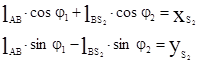(7)

Продифференцируем (7) по обобщенной координате и получим аналоги линейных скоростей точек S₂ в проекциях на оси х и у:

(9)

Глава 2. Анализ машинного агрегата.

В данной главе будут рассмотрены следующие вопросы:

1. Силы и моменты, действующие в машинном агрегате.

2. Переход от расчетных схем машинных агрегатов к динамическим моделям.

3. Расчет усилий в кинематических парах основного механизма рабочей машины.

4. Определение законов движения главного вала (входного звена) рабочей машины под действием приложенных сил и моментов при различных режимах работы машинного агрегата.

§2.1 Силы и моменты, действующие в машинном агрегате.

2.1.1 Движущиеся силы и моменты F_д и М_д.

Работа движущих сил и моментов за цикл положительна: А_д>0.

Цикл – промежуток времени, по истечению которого все кинематические параметры принимают первоначальное значение, а технологический процесс, происходящий в рабочей машине, начинает повторяться вновь.

2.1.2 Силы и моменты сопротивления (F_с,M_с).

Работа сил и моментов сопротивления за цикл отрицательна: А_c<0.

2.1.3 Силы тяжести (G_i).

Работа силы тяжести за цикл равна нулю: А_Gi=0.

2.1.4 Расчетные силы и моменты (Ф_Si,M_Фi).

Ф_Si,M_Фi – Главные векторы сил инерции и главные моменты от сил инерции.

2.1.5 Реакции в кинематических парах (Q_ij).

§2.2 Понятие о механических характеристиках.

Механическая характеристика 3-х фазного асинхронного двигателя.

Индикаторная диаграмма ДВС

H – ход поршня в поршневой машине

(расстояние между крайними

положениями поршня)

Индикаторная диаграмма насоса

Как правило, из паспорта известен диаметр поршня, по нему можно определить площадь S_п= p^.d²/4, тогда сила: F=p^.S_п

Правило знаков сил и моментов:

· Сила считается положительной, если она по направлению совпадает с направлением движения того звена, к которому эта сила приложена.

· Момент считается положительным, если его направление совпадает с направлением угловой скорости вращения данного звена.

Имея механическую характеристику поршневой машины и учитывая правило знаков, то можно перестроить в график сил (см. лабораторную работу №4).

Основной вывод:

В течение всего цикла работы поршневой машины сила, приложенная к поршню, будет изменяться как по величине, так и по направлению, это в свою очередь приводит к колебаниям угловой скорости главного вала рабочей машины.

§2.3 Понятие о расчетной схеме машинного агрегата и переход от нее к динамической модели.

На расчетной схеме машинного агрегата отмечают основные силовые факторы, действующие в машинном агрегате; основные массы звеньев, влияющих на закон движения машинного агрегата; и основные жесткости валов. На рис.5-92 показан переход от реальной схемы к расчетной схеме (а) и от нее к динамической модели.

Из множества масс выделены 3 основные, оказывающие самое большое внимание на закон движения.

Расчетная схема (б) – 3-х массовая динамическая модель.

Для описания закона движения 3-х массовой динамической модели необходимо 3 дифференциальных уравнения.

Если положить жесткость с₁ 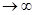, то можно перейти к двумассовой модели (необходимо 2 диф. уравнения).

Если положить жесткость с₂ 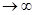, то получим одномассовую динамическую модель (рис. 2.3).

Рис. 2.3

Можно иметь 2 вида одномассовых динамических моделей:

1. Если звено приведения совершает вращательное движение, то одномассовая модель имеет вид

закон движения должен быть один,

поэтому w_м = w₁ , j_м = j₁

Уравнение движения можно записать одним уравнением, в виде изменения кинетической энергии:

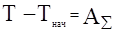
2. 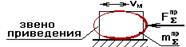Если звено приведения совершает поступательное движение, то одномассовая модель имеет вид:

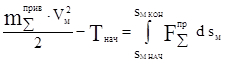
Этот вид рассматривать не будем.

§2.4 Приведение сил и масс к одномассовой динамической модели.

j₁ – обобщенная координата.

Нужно определить закон движения 1-го

звена данного механизма.

Дано: j₁, w₁, l_AB, l_BC, l_BS2, G₂, G₃, F₃, I_S1, I_S2.

Определить, как изменяется w₁.

При переходе от расчетной схеме к одномассовой механической модели за звено приведения, как правило, принимают то звено, закон движения которого определяют.

Звено приведения – зв.1; изобразим одномассовую модель:

2.4.1 Приведение масс.

При переходе от расчетной схемы к модели необходимо обеспечить равенство кинетической энергии звена приведенной модели и реального механизма:

Т_Мод = Т_Мех .

Кинетическая энергия модели должна быть равна кинетической энергии сего механизма.

Т_мод = Т_пост + Т_вращ

кинетическая кинетическая кинетическая