Рассеивающая (локализующая) способность электролитов

При протекании электрохимических реакций в условиях различных технологических процессов скорость электрохимической реакции может быть различной на различных участках электрода. В значительной степени это определяется распределением тока (плотности тока) по поверхности электрода. В свою очередь от плотности тока в соответствии с законом Фарадея зависит и скорость электрохимической реакции.

Распределение тока далеко не всегда равномерно. Это приводит к тому, что на различных участках поверхности могут достигаться различные значения потенциалов. Кроме того, когда скорость обработки определяется концентрационными ограничениями (в условиях замедленности стадии массопереноса) при различной толщине диффузионного слоя на разных участках поверхности достигаются различные значения плотности тока, а, следовательно, и скорости обработки.

В пределе это может приводить к такому положению, что определённые участки поверхности будут обрабатываться, т.е. на них будет протекать электрохимическая реакция, а на других нет. В таком случае говорят об электродах с неравнодоступной поверхностью или о системе с распределенными параметрами. Важно подчеркнуть, что в таких случаях могут наблюдаться размерные эффекты, т.е. свойства (например, возможность осуществления той или иной электрохимической реакции или изменение выхода по току) будут зависеть от размеров электродной поверхности.

В условиях электроосаждения (при использовании гальванических ванн) речь идёт о высокой или низкой рассеивающей способности электролитов. При высокой рассеивающей способности электролита электрод покрывается более равномерно, при низкой - происходит локализация процесса. В условиях ЭХРО электрохимический процесс должен быть максимально локализован, в то время как во многих гальванических процессах, наоборот, необходима высокая равномерность растворения. Иногда для описания этих процессов используется понятие кроющей способности электролита, которая измеряется в процентах и показывает какая доля поверхности электрода покрывается осадком.

Распределением тока, а, следовательно, рассеивающей и кроющей способностью электролитов необходимо управлять. Ниже будут изложены теоретические основы методов изучения распределения тока и управления им.

В общем случае подаваемое напряжение согласно закону Ома будет складываться из:

, (2.1)

в котором 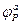и 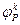- равновесные потенциалы для анодного и катодного процессов соответственно, 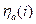и 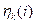- перенапряжения анодного 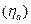и катодного 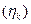процессов, IR – омическое падение напряжения между электродами.

Уравнение (2.1) показывает, что общее падение напряжения складывается из омического падения напряжения и падения напряжения в приэлектродных слоях.

Рассмотрим ванну или электрохимическую ячейку:

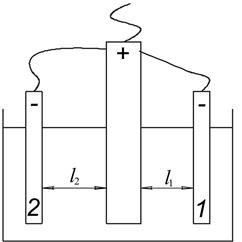
Рис. 2.1 Ванна с электродами, расположенными на разных расстояниях от анода (l₂ > l₁).

Будем считать, что напряжение постоянно, а электроды 1 и 2 включены параллельно. При­мем также для простоты линейную зависимость поляризации (перенапряжения) от плотности тока.

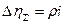(2.2)

Омическое падение напряжения будет определяться следующим образом: 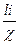, где - удельная электропроводность электролита. Учитывая равенство напряжений, получаем:

, (2.3)

в котором i₁ и i₂ плотности тока на электродах 1, расположенном на расстоянии l₁ от анода и 2, расположенном на расстоянии l₂ от анода, соответственно.

Из (2.3) получаем:

. (2.4)

Если 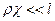, тогда:

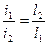(2.5)

т.е. в данном случае распределение плотностей тока обратно пропорционально расстоянию между электродами. Чем больше расстояние от электрода, тем меньше плотность тока.

Когда 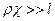получим, что , т.е. плотность тока не зависит от межэлектродного расстояния. Иными словами, в тех случаях, когда поляризационное сопротивление существен­но больше омического, должна наблюдаться максимальная равномерность распределения тока в электрохимической ячейке. Именно в этих случаях должна наблюдаться максимальная рассеивающая способность электролита, поскольку скорость процесса (плотность тока) не зависит от межэлектродного расстояния, а определяется только состоянием поверхности.

Рассмотренный выше случай является частным случаем линейной зависимости поляризации от плотности тока. Для более общего случая запишем уравнение тафелевской зависимости:

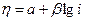(2.6)

Значение производной 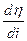теперь не постоянно, а является функцией плотности тока.

Параметр, который определяет тип распространения плотности тока, называется параметром Вагнера и определяется соотношением:

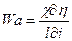(2.7)

При выполнении (2.6) параметр Вагнера имеет вид:

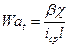(2.8)

Рассмотрим случаи, соответствующие различным значениям безразмерного параметра Вагнера:

если 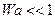, то это означает что итогда ;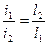

есл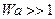и при 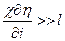,тогда .

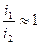Таким образом, параметр Вагнера количественно определяет тип распределения тока и, зная его величину, можно предложить возможные методы управления локализацией или равномерностью растворения (осаждения), в зависимости от типа распределения тока.