Основные определения

Выражение ,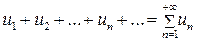

где 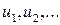– некоторые числа, называют числовым рядом, или просто рядом. Числа 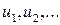называют членами ряда, а 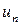– общим членом ряда. Ряд считается заданным, если существует правило, позволяющее находить по любому номеру 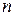соответствующий член ряда. Чаще всего это правило задается в виде формулы общего члена.

Сумма первых 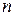членов ряда вида 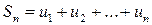называется n-ой частичной суммой.

Ряд называют сходящимся, если существует конечный предел последовательности частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают 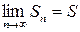. Если предел частичных сумм не существует или бесконечен, то ряд расходится. Сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования.

Если ряд сходится, то 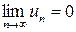– необходимое условие сходимости ряда. Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.