Тригонометрическая и показательная форма комплексного числа.
Понятие комплексного числа
Комплексное число имеет вид 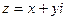 , где
, где 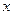 и
и 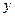 – действительные числа,
– действительные числа,
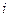 – мнимая единица,
– мнимая единица, 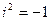
Число 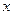 называется действительной частью (
называется действительной частью ( 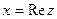 )комплексного числа
)комплексного числа 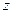 , число
, число 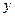 называется мнимой частью (
называется мнимой частью ( 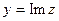 ) комплексного числа
) комплексного числа 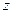 .
.
Геометрическая интерпретация комплексного числа.
. Комплексные числа изображаются на комплексной плоскости:

Комплексная плоскость состоит из двух осей:
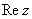 – действительная ось
– действительная ось
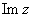 – мнимая ось
– мнимая ось
Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел.
Алгебраическая форма комплексного числа имеет вид 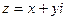 .
.
1.Сложение комплексных чисел. 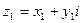 и
и 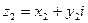
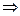
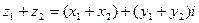
2. Вычитание комплексных чисел. 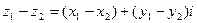
3. Умножение комплексных чисел. 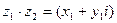 ·
· 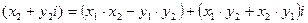
Деление комплексных чисел.
Тригонометрическая и показательная форма комплексного числа.
Любое комплексное число 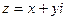 (кроме нуля) можно записать в тригонометрической форме:
(кроме нуля) можно записать в тригонометрической форме: 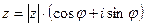 , где
, где 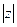 – это модуль комплексного числа, а
– это модуль комплексного числа, а 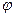 – аргумент комплексного числа. Изобразим на комплексной плоскости число
– аргумент комплексного числа. Изобразим на комплексной плоскости число 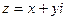 . Для определённости и простоты объяснений расположим его в первой координатной четверти.
. Для определённости и простоты объяснений расположим его в первой координатной четверти.
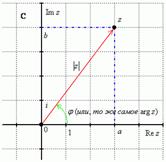
Модулем комплексного числа 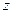 называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа z стандартно обозначают: 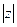 или r
или r
По теореме Пифагора модуль комплексного числа равен: 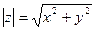 .
.
Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат.
Аргументом комплексного числа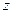 называетсяугол
называетсяугол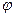 между положительной полуосью действительной оси
между положительной полуосью действительной оси 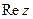 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 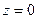 .
.
Аргумент комплексного числа 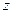 стандартно обозначают:
стандартно обозначают: 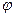 , где
, где 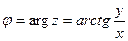 .
.
Дата добавления: 2017-01-29; просмотров: 853;
