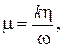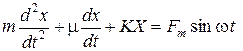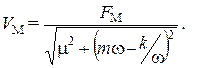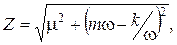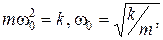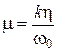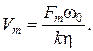НОРМИРОВАНИЕ ВИБРАЦИИ
Производственная вибрация подразделяется на техническую – это вибрация самого оборудования, и гигиеническую – это вибрация опорных поверхностей рабочих мест, фундаментов оборудования, кабин транспортных машин, ручек управления и инструмента, воздействующая непосредственно на человека.
Гигиеническая вибрация действует на человека в виде общей вибрации на весь организм и локальной вибрации, действующей главным образом на руки человека.
В свою очередь общая вибрация подразделяется на:
* транспортную, которая возникает в салоне или кабине машины при работе двигателя;
* транспортно-технологическую, которая возникает в кабине управления при работе грузоподъемных машин, выполняющих технологические операции в стационарном положении.
* технологическую, которая возникает при работе стационарных машин, станков, насосных агрегатов и другого оборудования.
В соответствии с ГОСТ 12.1.012-2004 ССБТ «Вибрационная безопасность.Общие требования». производится следующее нормирование гигиенической вибрации.
Весь нормируемый частотный диапазон вибрации заключен в 11 октавных полюсах со следующими среднегеометрическими значениями – ¦ср:
Таблица 5.1
| ¦ср, Гц | 31,5 | ||||||||||
| ¦1, Гц | 0,8 | 1,4 | 2,8 | 5,6 | 11,2 | 22,4 | |||||
| ¦2, Гц | 1,4 | 2,8 | 5,6 | 11,2 | 22,4 |
Частотные полосы (спектры) сформированы по принципу ¦1/¦2 = 2, и начиная с 8-ой полосы, третий знак сделан кратным 5 или 0. Среднегеометрическая частота ¦ср в каждой полосе определена по формуле :
_____
¦ср = Ö¦1¦2,
где ¦1 и ¦2 – граничные частоты, при этом отношение ¦1/¦2 = 2.
При больших частотах ¦ > 1400 Гц любая вибрация действует отрицательно на человека и не нормируется (не допускается).
Гигиеническое нормирование – это допустимый уровень виброскорости Um, воздействующий на человека при общей и локальной вибрациях.
Полоса с частотой ¦СР = 63 Гц считается базовой, при этом вибрации в других полосах сравнивают с вибрацией в базовой полосе.
Из рис. 5.1 и 5.2 видно, что наибольшую опасность представляет общая вибрация, действующая на весь организм, так как допустимая область общей вибрации и по абсолютным значениям уровней виброскорости и по площади занимаемой на графике значительно меньше тех же параметров в локальной вибрации. Некоторые критические величины вибрации, действующие на человека: f = 0.7 Гц – морская болезнь, f = 6...9 Гц – резонанс внутренних органов, f = 25 Гц – резонанс головы человека.
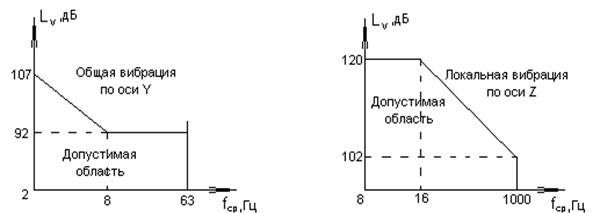
Рис. 5.1. Общая вибрация Рис. 5.2. Локальная вибрация
в производственных помещениях
По направлению действия на человека различают вибрацию вертикальную, действующую вдоль тела по позвоночнику – ось Z, горизонтальную, действующую перпендикулярно грудной клетке – ось Х, и горизонтальную, действующую по плечевому поясу – ось Y. Наибольшую опасность представляет вибрация, действующая по оси Y по плечевому поясу, например, в кабинах транспортных машин, в которых вибрация распространяется в горизонтальном направлении по осям X и Y.
При локальной вибрации, действующей на руки при работе, например с пневмомолотком, ось Z совмещается с направлением усилия работающего (сверху вниз), а ось X совмещается с осью обхвата рукой рукоятки, ось Y в этом случае не нужна.
5.3. АНАЛИЗ ПРОСТЕЙШЕЙ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ
В общем виде для одномассовой колебательной системы существуют шесть степеней свободы, n = 6, из которых три степени имеют продольные направления вдоль осей Х, Y и Z, а другие три имеют крутильные направления относительно соответствующих осей.
Рассмотрим простейшую одномассовую колебательную систему с одной степенью свободы, действующей по оси X, с пружиной растяжения, жестко закрепленной на одном конце (рис. 5.3.).
 |
Рис. 5.3. Колебательная система:
1 – упругий элемент – пружина растяжения с коэффициентом жесткости К, Н/м;
2 – масса колебательной системы m, кг; 3 – сопротивление колебательной системы
с коэффициентом сопротивления m, H×с/м; х, v – смещение и скорость колебательного
процесса, мм, мм/с; 4 – сила внешнего воздействия FВ, H
Определим силы, действующие в колебательной системе.
Сила инерции из 2-го закона Ньютона: FU = ma, (а - ускорение массы, м/с2).
Сила упругости пружины FУП = ХК, H.
Сила сопротивления колебательной системы FС = um.
Коэффициент сопротивления системы определяется, Н×с/м.
|
где h – коэффициент трения колебательной системы, включает в себя внешнее трение (вязкость масла в подшипниках, трение в электромагнитном поле) и внутреннее трение (трение в металлах, из которых изготовлены детали машины).
Сила внешнего воздействия: FВ = Fmsin (wt + j0).
где Fm – амплитуда внешней силы, H; w – угловая частота колебательного процесса, Гц; t – время, с; j0 – начальная фаза колебательного процесса, град.
Произведем сложение всех сил, результат представим в дифференциальной форме. Начальную фазу j0 не учитываем.
|
(5.2)
Это уравнение простейшей колебательной системы. Решение этого уравнения после подстановки в него величины смещения х в комплексной форме
х = АМejwt дает выражение для определения амплитуды виброскорости колебательного процесса, м/с.
|
(5.3)
Знаменатель представляет собой полное сопротивление системы - импеданс, H×c/м.
|
, ( 5.4)
где m – активное сопротивление; mw – k/w – реактивное сопротивление; mw – инерционная составляющая реактивного сопротивления; k/w – упругая составляющая реактивного сопротивления.
Определим амплитуду виброскорости в различных областях работы машины.
· Резонансная область работы машины, w = w 0 . Известно, в резонансе реактивное сопротивление равно 0, т.е. инерционная и упругая составляющие равны между собой, mw0 – k/w0 = 0,
|
отсюда
где w 0 – резонансная угловая частота вращения машины.
|
ляя , получаем
|
(5.5)
· Зарезонансная область работы машины, т.е. w > w 0 . Тогда mw > k/w.
В случае незначительной величины m полное сопротивление принимается равным инерционному:
Z = mw , тогда, подставляя Z в (5.3), получим:
Vm = F / mw. (5.6)
· Дорезонансная область работы машины, т.е. w < w0 . Тогда mw < k/w .
При m близкой к нулю Z = k /w , а выражение (5.3) принимает вид:
Vm = Fmw/к, (5.7)
Из (5.5), (5.6), (5.7) следуют выводы:
Во всех областях работы вращающихся машин для снижения вибрации, т.е. для уменьшения величины Vm, следует прежде всего уменьшать величину внешней силы Fm .
В резонансной области снижение вибрации достигается увеличением активного сопротивления: либо за счет увеличения жесткости колебательной системы k , либо за счет увеличения коэффициента трения h внешнего, например в подшипниках, или внутреннего в металлах, из которых изготавливается машина (5.5).
В зарезонансной области снижение вибрации достигается увеличением массы колебательной системы m , как правило, увеличением массы фундамента (5.6).
В дорезонансной области снижение вибрации достигается увеличением жесткости колебательной системы k (5.7).
Увеличение частоты вращения машины w в дорезонансной и резонансной областях работы приводит к увеличению вибрации (5.5 и 5.7). Увеличение частоты вращения машины в зарезонансной области работы приводит к уменьшению вибрации (5.7).
Сделанные выводы по снижению вибрации в различных областях работы машины можно представить графически на рис. 5.4.
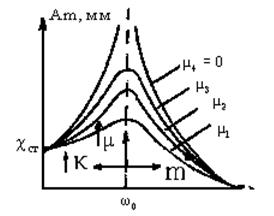
Рис. 5.4. Резонансные характеристики колебательной системы:
m1 > m2 > m3> m4 = 0; Xст = Fm/K – статический прогиб ротора машины при w = 0
Из рис. 5.4 следует, что наибольший эффект снижения вибрации достигается в резонансной области увеличением активного сопротивления m. В до и зарезонансных областях – увеличением параметров К и m – соответственно.
Дата добавления: 2017-01-29; просмотров: 1345;