Круговая геометрия измерений в ТВТ

Рассмотрим задачу восстановления двумерного распределения коэффициента ослабления излучения 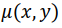(рис. 17).

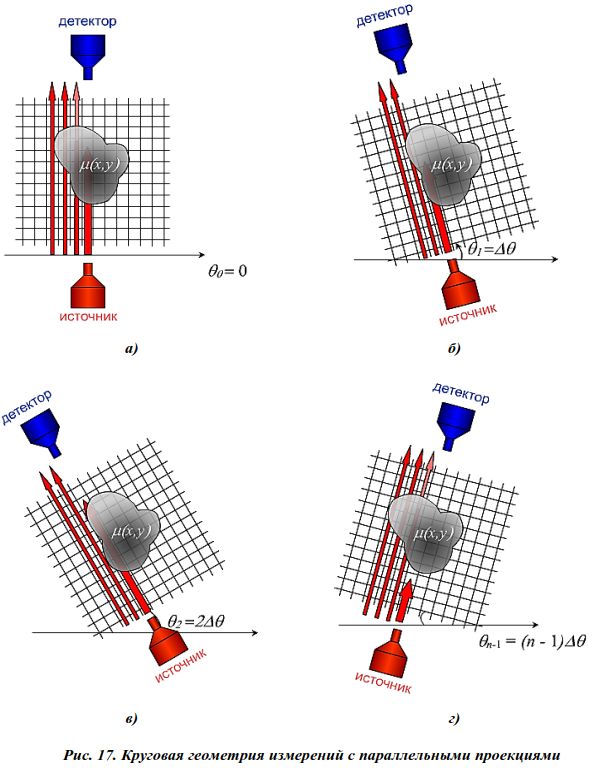
Процесс измерений выглядит следующим образом. Источник излучения, формирующий «карандашный» пучок, проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «источник-детектор» поворачивается относительно объекта на некоторый угол и снимается новый набор отсчетов, определяющий следующую проекцию.

Такие измерения повторяются, пока система «источник-детектор»

не повернется на угол 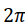. По полученному набору одномерных проекций необходимо восстановить двумерное распределение.

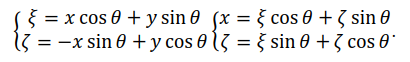
Поскольку система «источник-детектор» вращается вокруг объекта, такая схема измерений называется круговой геометрией измерений, а так как для получения следующего отсчета в проекции пучок смещается параллельно предыдущему положению, проекции называют параллельными проекциями. Для математического описания связи проекций с искомым распределением 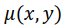наряду с неподвижной системой координат 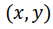введём вращающуюся систему координат 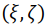(рис. 18):

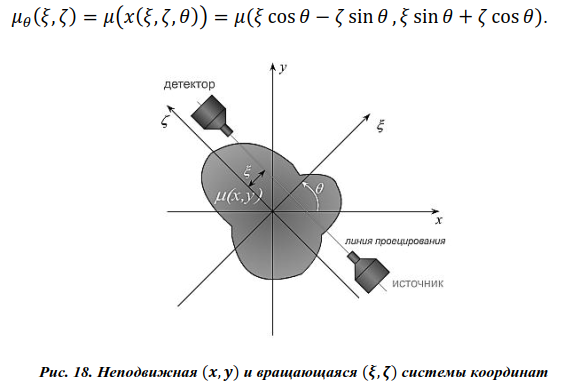
Обозначим через 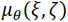распределение линейного коэффициента ослабления в системе координат 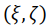, повернутой относительно неподвижной системы координат на угол :

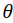В частности, .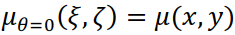

Для интенсивности 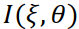излучения, прошедшего через объект, в

соответствии с выражениями, приведенными в разд. 1.1, получим:

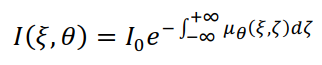
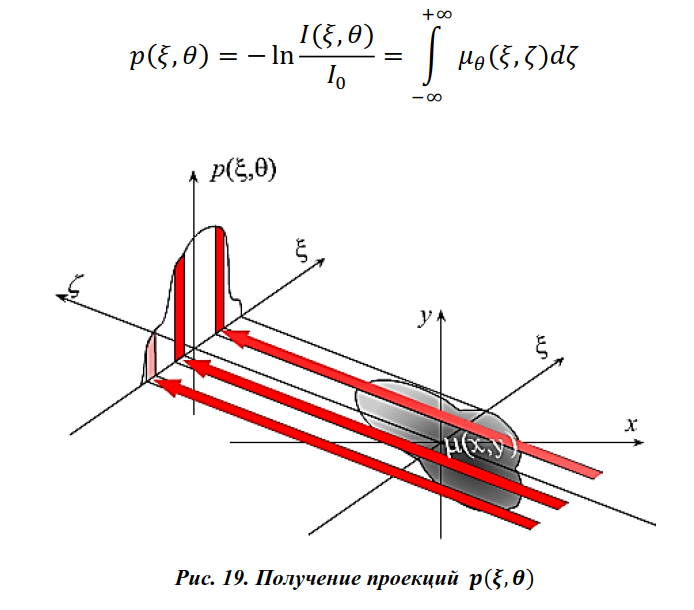
Назовем проекцией 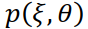следующую величину (рис. 19):

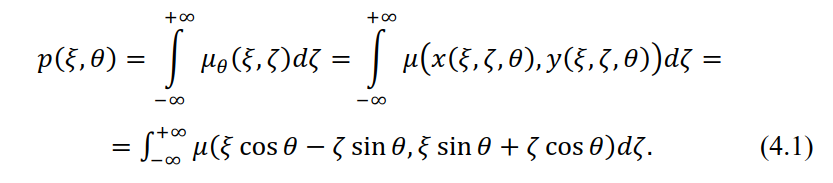
Таким образом, получим следующее выражение для проекции:

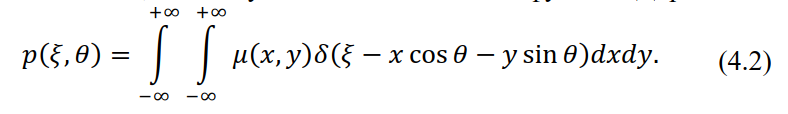
Соотношение (4.1) называется преобразованием Радона двумерной функции. В дальнейшем нам понадобится другое представление для преобразования Радона, использующее свойства дельта-функции Дирака:

Происхождение представления (4.2) становится понятным, если вспомнить, что дельта функция будет равна нулю везде, кроме прямой

.

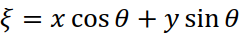Метод двумерной фильтрации (метод ро-фильтрации)

Задачей вычислительной томографии является восстановление неизвестной функции нескольких (не менее двух) переменных по известным интегралам от нее меньшей размерности. В частности, в двумерном случае необходимо восстановить функцию 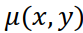по проекциям 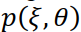, связанным с искомой функцией преобразованием Радона (4.1) или (4.2). С математической точки зрения необходимо указать метод обращения интегрального преобразования (4.1) или (4.2). Рассмотрим в первую очередь один из таких методов, получивший название метода ро- фильтрации или метода двумерной фильтрации [11, 17].

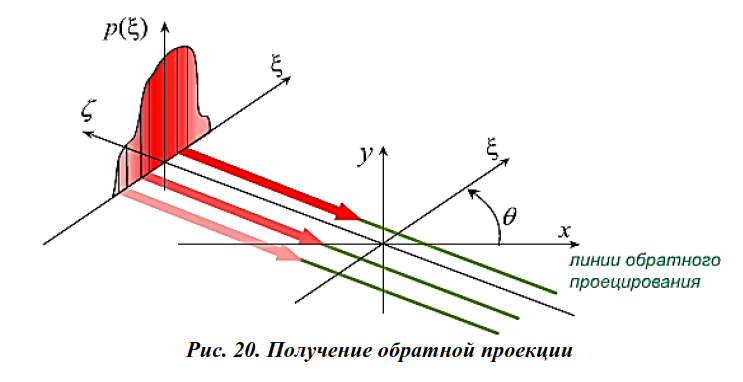
Метод ро-фильтрации состоит из двух этапов. На первом этапе с по- мощью операции обратного проецирования получают так называемое суммарное изображение. На втором этапе суммарное изображение подвергается двумерной фильтрации, результатом которой является оценка искомого изображения, например, двумерного распределения коэффициента ослабления излучения в объекте. Суть операции обратного проецирования заключается в получении двумерной функции – суммарного изображения, исходя из набора одномерных проекций.

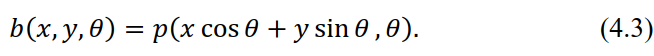
При обратном проецировании сначала для каждой проекции 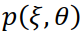находится так называемая обратная проекция :

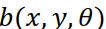Смысл обратной проекции заключается в том, что одномерная проекция 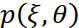как бы «размазывается» на всю двумерную плоскость перпендикулярно оси 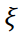(рис. 20).

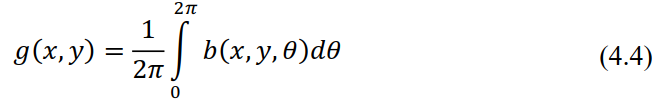
Таким образом, значение отсчета приписывается всем точкам, лежащим на прямой 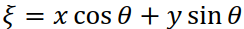(в неподвижной системе координат). Суммарное изображение 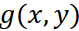получается наложением всех обратных проекций:

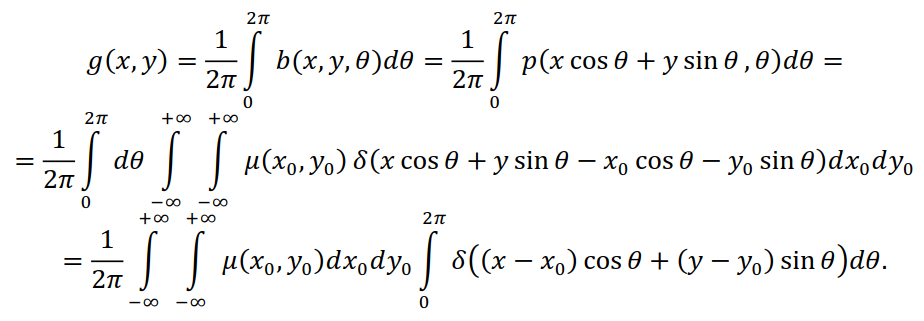
Для нахождения связи суммарного изображения 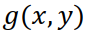с искомой функцией 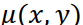подставим в (4.4) определение обратной проекции (4.3) и проекции (4.2):

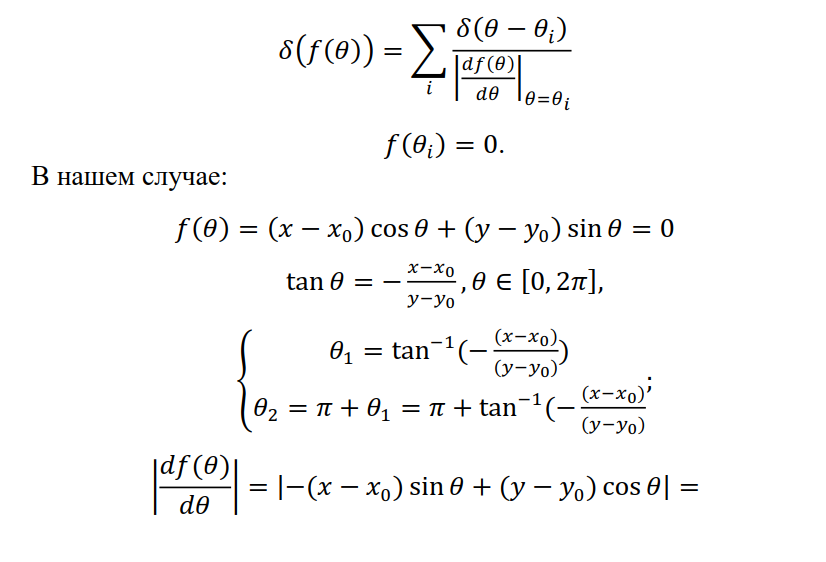
Чтобы вычислить интеграл по 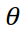, нужно использовать свойство функции от сложного аргумента:

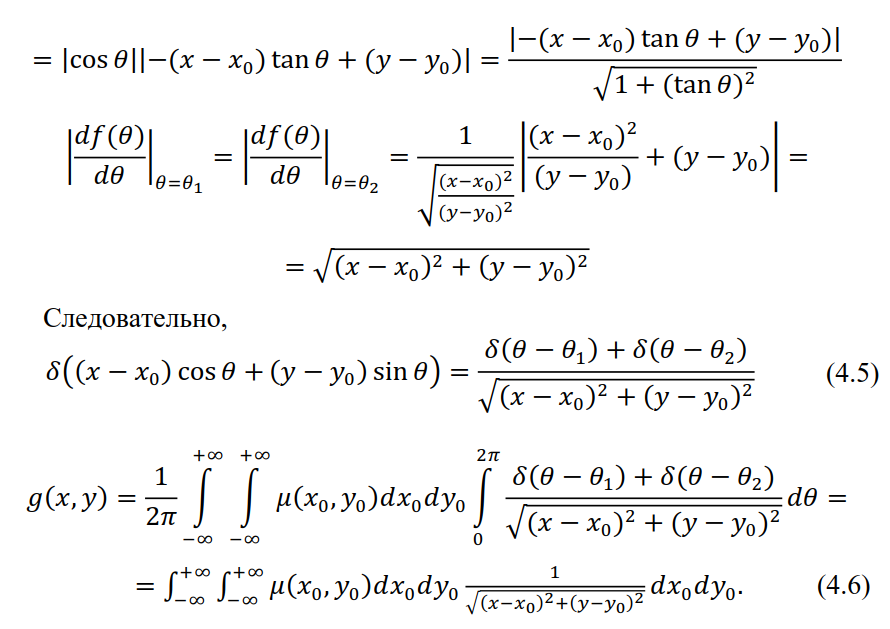
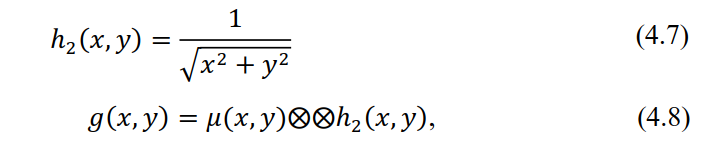
Таким образом, суммарное изображение 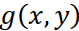является двумерной сверткой искомой функции с некоторым ядром 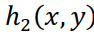, а именно:

где 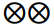– знак двумерной свертки.

Теперь становится понятной необходимость дополнительной операции фильтрации суммарного изображения, т.е. решения свертки с известным ядром, либо еще одной свертки с некоторым другим ядром 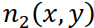, что, как увидим, является одним и тем же. Для решения свертки (4.8) воспользуемся теоремой о (двумерной) свертке:

В формуле (4.9) мы записали оценку вместо истинного изображения

по следующей причине. При измерениях проекции фиксируются с некоторой ошибкой измерений, следовательно, и суммарное изображение

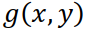, и восстановленное по формуле (4.9) изображение будет получено с некоторой ошибкой. Кроме того, если Фурье-образ ядра 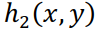будет иметь близкие к нулю значения, то мы можем получить оценку 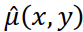сколь угодно сильно отличающуюся от истинного изображения 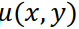, что является отражением общей некорректности задачи решения интегральных уравнений первого рода, к которым относится свёртка.

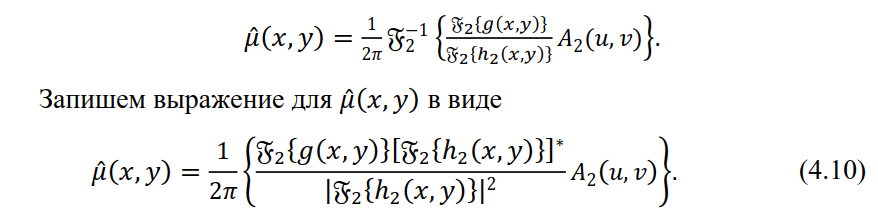
При реальных вычислениях вводят аподизирующую функцию 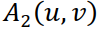(функцию окна) в Фурье-пространстве ( 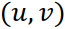– декартовы координаты в Фурье-пространстве). Аподизирующая функция учитывает априорную информацию об исходной функции и регуляризирует некорректную задачу решения свёртки. С помощью аподизирующей функции, например, можно исключить нежелательное влияние близких к нулю значений Фурье-образа ядра свертки 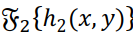что обеспечит большую близость оценки 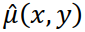к истинному изображению 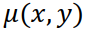. Таким образом, регуляризированная оценка искомого изображения вычисляется по следующей формуле:

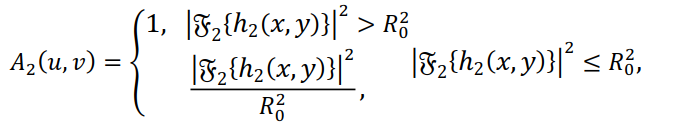
где * – знак комплексного сопряжения. Тогда, например, можно взять следующую аподизирующую функцию:

т.е. если модуль Фурье-образа ядра 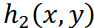больше некоторой выбранной заранее константы 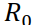, то никакой коррекции не производится, в противном случае модуль Фурье-образа ядра заменяется на эту константу. Тогда

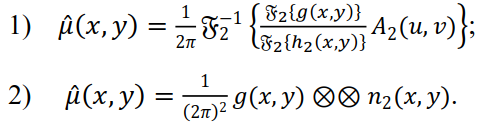
Таким образом, получаем два представления:

Какое из этих представлений использовать, зависит от того, насколько быстро выполняются реальные вычисления свёртки и преобразования Фурье. Так как Фурье-образы от известных функций могут быть вычислены заранее, то необходимо сопоставить скорость выполнения одной свёртки со скоростью выполнения двух преобразований Фурье и одной операции умножения.

В заключение вычислим Фурье-образ 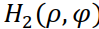функции ядра. Вводя полярные координаты