Элементы объема, изображения и числа Хаунсфилда

В вакууме все фотоны рентгеновского излучения, которые вылетают

из источника в направлении детектора, достигают последнего. Когда между источником и детектором помещено какое-нибудь вещество, некоторая часть фотонов, покидающих источник в направлении детектора, последнего не достигнет, так как они либо поглощаются, либо рассеиваются. Вероятность того, что фотон будет удален из первичного пучка, определяется энергией данного фотона и характеристиками вещества, которое находится между источником и детектором рентгеновского излучения.

Линейный коэффициент ослабления ткани определяют следующим образом. Пусть p – вероятность того, что фотон с энергией 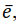, который входит в однородный слой ткани перпендикулярно поверхности дан- ного слоя L, не поглотится и не рассеется в этом слое, т.е. p – степень пропускания данным слоем фотона с энергией 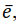в направлении L. Определим

где ln означает натуральный логарифм. Отметим, что величинлинейного коэффициента ослабления зависит от используемых единиц длины. Линейный коэффициент ослабления рентгеновского излучения измеряют в единицах, обратных единице длины. Например, линейный коэффициент ослабления рентгеновского излучения с энергией 73 кэВ для воды равен 0,19 см-1.

В дальнейшем будем использовать так называемое относительное линейное ослабление рентгеновского излучения при энергии 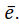. Для любой точки пространства относительное линейное ослабление равно 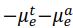, где t – ткань, которая находится в данной точке пространства во время рабочих измерений, и а – вещество, которое находится в этой же точке во время калибровочных измерений. Так как пространство за пределами поля реконструкции остается неизменным во время проведения рабочих и калибровочных измерений, то относительное линейное ослабление для всех точек, находящихся вне поля реконструкции, равно нулю для рентгеновского излучения с любой энергией. Заметим также, что для любой точки, которая находится внутри поля реконструкции, величина 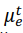имеет одинаковое значение, так как можно считать, что эталонный материал является однородным и не изменяется во время калибровочных измерений.

Теперь допустим, что нас интересует слой толщиной 1,3 см в теле пациента. Весь этот слой можно подразделить на небольшие участки длиной 1,3 см с одинаковым сечением в форме квадрата. Такие участки обычно называют элементами объема или, сокращенно, элобами. Грубо говоря, число Хаунсфилда пропорционально среднему значению относительного линейного ослабления в элобе. Так как относительное линейное ослабление зависит от энергии рентгеновского излучения, такое определение нуждается в дополнительном разъяснении и уточнении, которое будет дано в следующем разделе. Обычно принимают за фоно- вый материал воду (число Хаунсфилда для нее считают равным нулю), а масштаб чисел Хаунсфилда выбирают таким, чтобы это число для воздуха равнялось 1000 (или в другом масштабе 500).

Предположим для примера, что поле реконструкции представляет собой квадрат 41,6×41,6 см, а размеры элоба равны 1,3×0,13×0,13 см. Тогда имеется матрица, состоящая из 320×320 таких элобов, которые полностью заполняют всю область реконструкции и образуют матрицу, состоящую из 320×320 чисел Хаунсфилда. При отображении томограммы на дисплей выводятся соответствующие числа Хаунсфилда. В идеале хотелось бы видеть массив из 320×320 маленьких квадратиков с одинаковым внутри каждого из них почернением, пропорциональным числу Хаунсфилда данного элоба в данной точке. Эти маленькие квадратики называют элементами изображения или (сокращенно) элизами.

Требования к томографу:

1) получать произвольно ориентированные сечения; 2) обеспечивать нужную лучевую нагрузку;

3) время измерений;

4) достоверность получаемых результатов.