Шестерню в конической передаче часто располагают консольно.
Аналогом начальных и делительных цилиндров цилиндрических зубчатых передач в конических передачах являются начальные и делительные конусы.
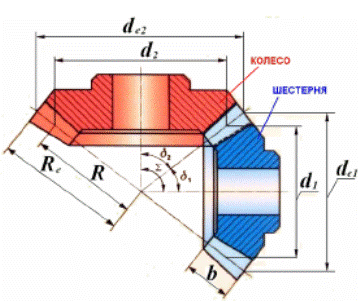
У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают 2 окружных модуля:
m- средний делительный окружной модуль(в среднем сечении)
me- внешний делительный окружной модуль(на внешнем торце зуба)
средние делительные диаметры:
d1 = mz1 гдеz1 и z2- числа зубьев шестерни и колеса
d2 = mz2
внешние делительные диаметры:
de1 = mez1
de2 = mez2
внешнее конусное расстояние:
de = 0.5me√z1²+z2²
среднее конусное расстояние:
R = Re – 0.5b
углы делительных конусов:
шестерни-δ1
колеса-δ2
tg δ1 = z1/z2 δ2 = 90˚- δ1
передаточное число конической зубчатой передачи:
u = ω1/ω2 = n1/n2 =z2/z1 = d2/d1 = de2/de1 = tgδ2 = 1/tgδ1
Вместо конических передач в машиностроении часто используют так называемые гипоидные передачи. Они предназначены для передачи вращения между перекрещивающимися геометрическими осями валов.
Раздел №4: Червячные передачи.
Это передачи зацепления. Червячные передачи применяются для передачи вращающего движения между валами при угле перекрещивания их осей θ = 90˚.
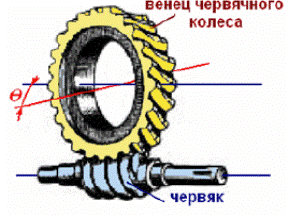Червяк- это короткий винт с трапецеидальной нарезкой.
Червячная передача – это зубчато-винтовая передача, движение в которой осуществляется по принципу винтовой пары.
ДОСТОИНСТВА ЧЕТВЯЧНОЙ ПЕРЕДАЧИ:
- возможность получения большого передаточного числа в одной ступени(umax = 80)
- компактность и сравнительно небольшая масса конструкции
- плавность и бесшумность работы
- возможность получения самотормозящей передачи, т.е. допускающей движение только от червяка к колесу.
НЕДОСТАТКИ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ:
- низкий КПД. Рекомендуемая мощность до 100кВт
- необходимость применения для венцов червячных колес дорогих антифрикционных материалов.
- повышенное изнашивание из-за высоких скоростей скольжения.
КЛАССИФИКАЦИЯ ЧЕРВЯЧНЫХ ПЕРЕДАЧ:
(в зависимости от формы внешней поверхности червяка)
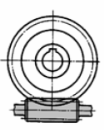с цилиндрическим червяком (образующая червяка- прямая линия).Такие червяки проще в изготовлении.
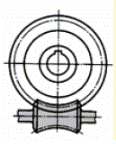
с глобоидным червяком (образующая- прямая линия). Имеет большую нагрузочную способность.
В зависимости от направления линии витка червяка:
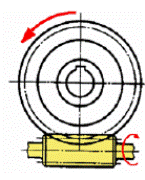правое направлениелевое направление линии ветка
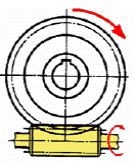линии витка
В зависимости от расположения червяка относительно колеса:
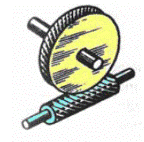с нижним расположением червяка(при окружной скорости не более 5м/с)
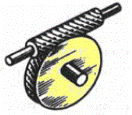
с верхнем расположением червяка(допускают окружную скорость более 5м/c)
с боковым расположением червяка
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ:
Геометрические размеры червяка и колеса определяются по формулам, аналогичным для зубчатых колес.
В червячной передачи расчетным является осевой модуль червяка m, равный торцовому модулю червячного колеса.
ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ ЧЕРВЯКА:
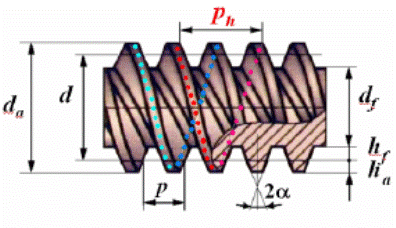
Делительный диаметр d, т.е. диаметр такого цилиндра червяка, на котором толщина витка равна ширине впадины d = mq, где q- коэффициент диаметра червяка (число модулей в делительном диаметре червяка)
ha-высота головки витка червяка и зуба колеса ha = m
hf- высота ножки витка червяка и зуба колеса hf = 1.2m
df-диаметр впадин витков df = d-2hf = d-2.4m
da- диаметр вершин витков da = d+2ha = d+2m
2α- угол профиля витка в осевом сечении α =20˚ 2α = 40˚
p- расчетный шаг четвяка p = πm
ph- ход витка ph = pz1, где z1- число витков червяка
количество витков червяка предусмотрены стандартом:z1 =1,2,4….
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ЧЕРВЯЧНОГО КОЛЕСА:
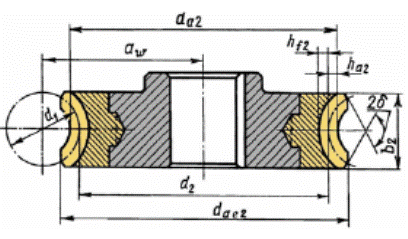
Геометрические параметры зубчатого венца червячного колеса определяется в среднем сечении по формулам, подобным формулам для цилиндрического зубчатого колеса.
делительный диаметрdz = mz2
диаметр вершин зубьевda2 = d2+2m
диаметр впадин зубьевdf2 = d2-2.4m
ширина венцаb2 = 0.355aw
наибольший диаметр червячного колесаdae2 ≤ (da2+6m)/(z1+2)
передаточное число зубчатой передачиu = ω1/ω2 = n1/n2 =z2/z1
n1 n2 –частоты вращения червяка и колеса
z1-число витков червяка
z2- число зубьев колеса
Дата добавления: 2016-05-11; просмотров: 677;