Циліндричний сосуд(посудина) під дією внутрішнього тиску р
Складний опір
Під складним опором розуміють різні комбінації раніше розглянутих простих видів навантаження (розтягу-стиску, зсуву, кручення та згину).
При аналізі складного опору справедливі принцип суперпозиції, принцип незалежності дії сил.
Складний та косий згини
Складний згин спричиняється силами або моментами, розташованими в різних площинах, які проходять крізь вісь балки. Такий згин зветься також неплоским згином, оскільки зігнута вісь балки не є плоскою кривою.
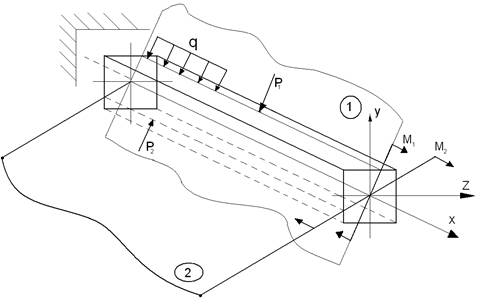
1 та 2— силові площини.
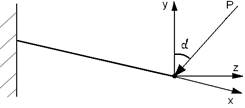
Якщо всі навантаження, що спричиняють згин, діють в одній площині, що не збігається ні з однією з головних площин, то згинання зветься косим.
Як у випадку неплоского, так і у випадку косого згину, найзручніше зводити згини до двох плоских.
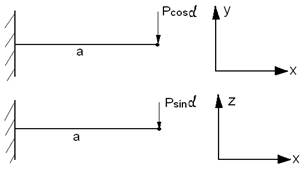
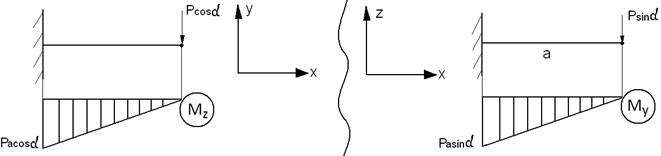
Обчислимо напруження в деякій точці (y,z) довільного поперечного перерізу, розмістивши її для певності в першому квадранті. Напрями головних осей показані на рисунку. Згинальні моменти будемо вважати додатними, якщо вони спричинюють у точках першого квадранта розтягуюче напруження.
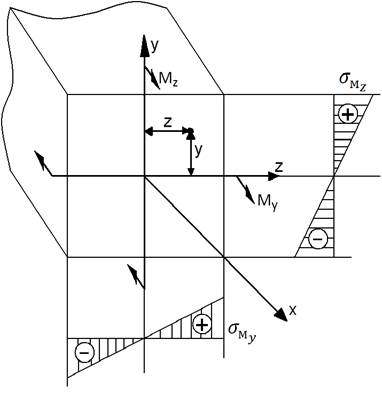
Виходячи з принципу суперпозиції, знайдемо напруження в зазначеній точці, розглядаючи два плоских згини.
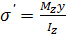 ;
; 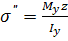
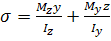 (1)
(1)
Нормальні напруження при складному згині.
У випадку косого згину
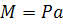
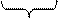
|
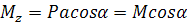

Рівняння нейтральної лінії при складному згині в будь-якому поперечному перерізі дістанемо з формули (1), поклавши 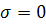
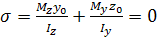 (3)
(3)
y0, z0 —координати точок нейтральної лінії.
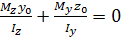 – рівняння прямої, що проходить крізь початок координат (центр ваги перерізу).
– рівняння прямої, що проходить крізь початок координат (центр ваги перерізу). 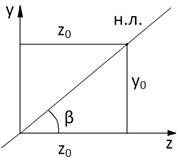
Положення нейтральної лінії характеризується її кутовим коефіцієнтом: 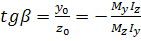 (4)
(4)
У формулі (4), кут вважається додатним, якщо відраховується від осі Z проти годинникової стрілки. Для моментів, у формулі (4), знаки моментів такі, як за правилом І квадранта.
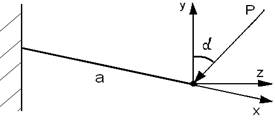
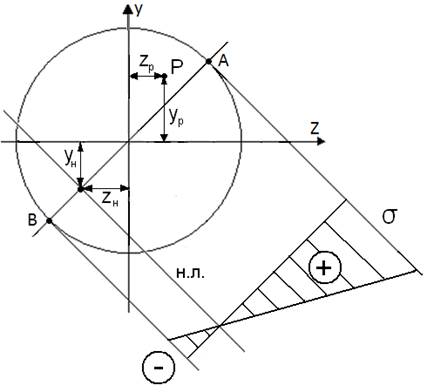
Якщо у деякому перерізі бруса, де діють найбільші згинальні моменти 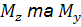 треба знайти положення нейтральної лінії, то зручно спочатку показати положення силової лінії Р-Р.
треба знайти положення нейтральної лінії, то зручно спочатку показати положення силової лінії Р-Р.
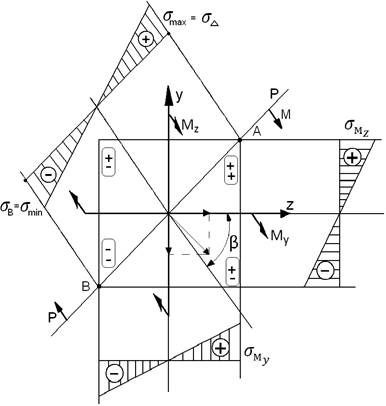
Нейтральна лінія не перпендикулярна силовій площині, перпендикулярна тільки вектору моменту.
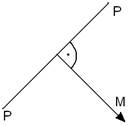
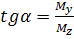 – кут нахилу силової площини.
– кут нахилу силової площини.
Тоді 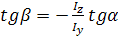 після находження положення нейтральної лінії будуємо епюру напружень та визначаємо положення небезпечних точок А і В.
після находження положення нейтральної лінії будуємо епюру напружень та визначаємо положення небезпечних точок А і В.
Умова міцності для небезпечних точок:
|
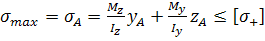
 |
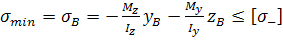
У загальному вигляді неплоского згину умова згину має вигляд:
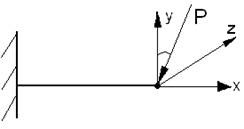
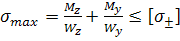
Розглянемо балку:
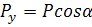 ;
;
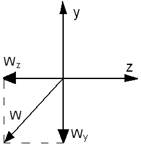 Прогин за віссю Y:
Прогин за віссю Y: 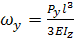
Прогин за віссю Z: 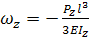
Повний прогин: 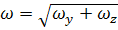
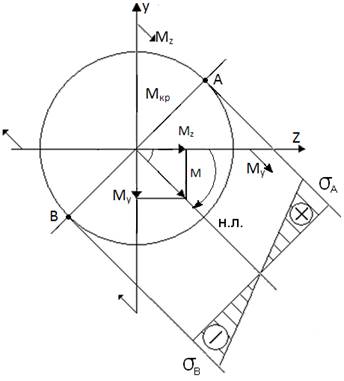 Складний згин балки круглого перерізу:
Складний згин балки круглого перерізу:
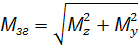
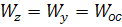 ;
; 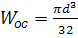
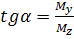
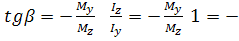
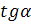
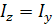
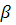 відкладаємо за годинниковою стрілкою, тобто від осі Z. Тоді нейтральна лінія проходить через вектор моменту М.
відкладаємо за годинниковою стрілкою, тобто від осі Z. Тоді нейтральна лінія проходить через вектор моменту М.
Умова міцності:
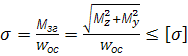
Порядок розрахунку:
1. Визначаємо положення небезпечної точки по довжині балки.
2. У знайденої небезпечної точки розглядаємо переріз балки і визначаємо небезпечні точки в перерізі.
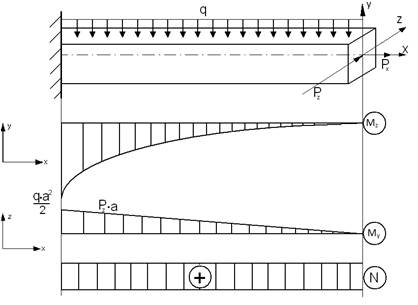 Згин з розтягом (стиском)
Згин з розтягом (стиском)
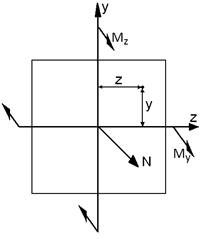
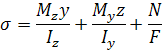
Для визначення положення нейтральної лінії:
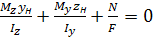
|
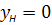 ;
; 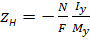
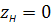 ;
; 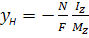
Умова міцності: 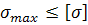
Якщо переріз симетричний: 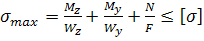
Для круглого проділу:
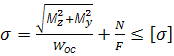
Позацентровий розтяг (стиск) прямого бруса
Позацентровий розтяг (стиск) є окремим випадком складного згину з розтягом (стиском), при якому брус розтягується силами паралельними осі бруса, так що рівнодіюча їх не збігається з віссю бруса, а проходить крізь точку Р, що називається полюсом сили.
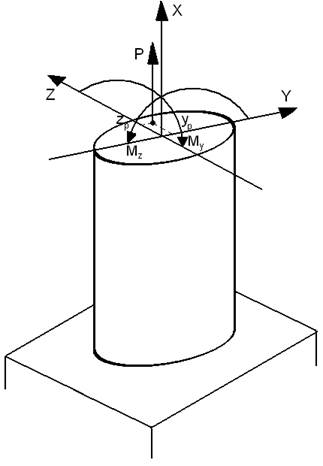
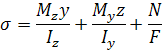
N=P; 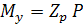 ;
;
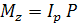
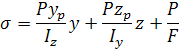
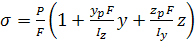 =
=
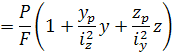
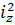 =
= 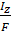 ;
; 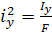 – радіуси інерції.
– радіуси інерції.
Рівняння нейтральної лінії:
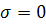
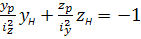
Відрізки, що відсікаються нейтральною лінією
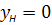 ;
; 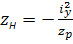 ;
;
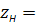 0 ;
0 ; 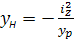 ;
;
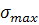 =
= 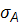 =
= 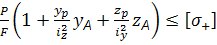
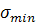 =
= 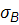 =
= 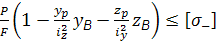
Для прямокутного перерізу:
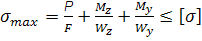
Можна визначити зону таких віддалень сили Р від осі, при яких нормальні напруження по всьому поперечному перерізу будуть одного знака. Така зона називається перерізомядра. Це важливо для брусів з матеріалів, що погано чинять опір розтягу (наприклад для цегляної кладки, бетону та сірого чавуну).
Отже, ядром перерізу називають зону навколо центра ваги поперечного перерізу, яка має таку властивість: якщо позацентрово-прикладене навантаження розташоване в зоні ядра, то нормальні напруження в усіх точках поперечного перерізу мають один знак.
Лекція № Складний опір (продовження)
Згин з крученням круглих та прямокутних стержнів
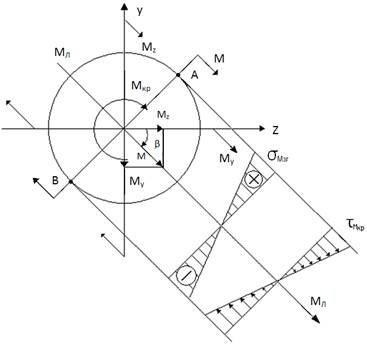
У перерізі діють одночасно крутний момент Мкр та згинальні моменти Мz та Мy . Визначимо сумарний згинальний момент:
Мзг = 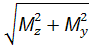 , положення нейтральної лінії
, положення нейтральної лінії
tg 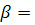 -
- 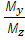
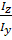
(кут 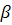 додатній, якщо відкладається проти годинникової стрілки від осі z).
додатній, якщо відкладається проти годинникової стрілки від осі z).
Побудуємо епюри напружень від внутрішніх силових факторів. В небезпечній точці А:
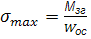 =
= 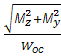
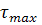 =
= 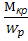
 Якщо в небезпечній точці А виділити елемент матеріалу, то він буде знаходитися у плоскому напруженому стан і розрахунок на міцність треба проводити по теорії міцності:
Якщо в небезпечній точці А виділити елемент матеріалу, то він буде знаходитися у плоскому напруженому стан і розрахунок на міцність треба проводити по теорії міцності:
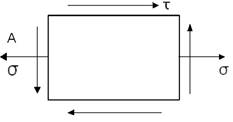
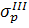 =
= 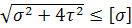
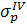 =
= 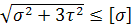
Теорія Мора:
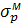 =
= 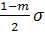 +
+ 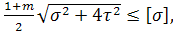 m=
m= 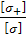
( 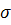 - нормальні напруження, які викликає згин;
- нормальні напруження, які викликає згин; 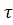 - дотичні, які викликає кручення).
- дотичні, які викликає кручення).
Підставляючи значення 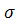 та
та 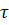 в небезпечній точці А (тут вони досягають максимальних значень), тобто:
в небезпечній точці А (тут вони досягають максимальних значень), тобто:
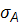 =
=  ;
; 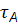 =
= 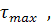 враховуючи
враховуючи 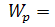 2W.
2W.
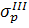 =
= 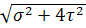 =
= 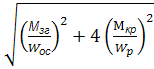 =
= 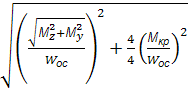 =
= 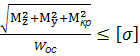
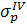 =
= 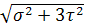 =
= 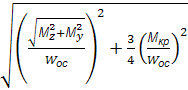 =
= 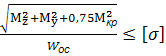
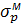 =
= 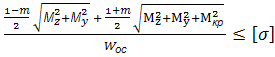
Можна відмітити, що всі умови міцності можна звести до одного:
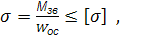 де
де 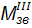 =
= 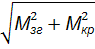 =
= 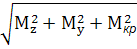
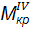 =
= 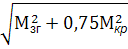 , де Мзг
, де Мзг 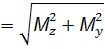
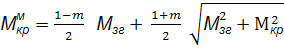
Всі формули справедливі для кільцевого перерізу:
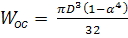
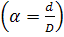
Згин з крученням прямокутних стержнів
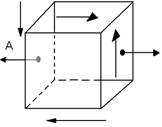
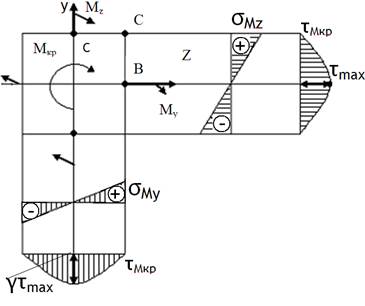 Епюри нормальних та дотичних напружень показують, що на відміну від круглого перерізу у розглядуваному випадку σmax та τmax мають місце не в одній і тій же точці найбільш небезпечними будуть точки А,В та С
Епюри нормальних та дотичних напружень показують, що на відміну від круглого перерізу у розглядуваному випадку σmax та τmax мають місце не в одній і тій же точці найбільш небезпечними будуть точки А,В та С
Т.«А» 
Елемент, виділений в точці А знаходиться у лінійному напруженому стані і тут діють σMz та σMy.
Умова міцності: σ= 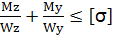
Аналогічно в протилежній точці, де буде стиск.
Для т.“ В,С” 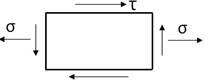
Елементи в області точок В та С знаходяться у плоско напруженому стані і розрахункові напруження в цих точках записується за III, IV,V теоріями міцності.
Наприклад в точці В за IV теорією міцності
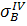 =
= 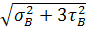 =
= 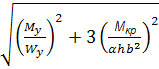
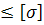
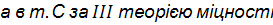
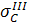 =
= 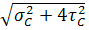 =
= 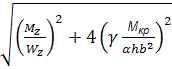
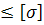
Записані умови міцності дозволяють проводити перевірочний і проектувальний розрахунки. Найбільш небезпечна точка з трьох визначається тільки за результатами обчислень.
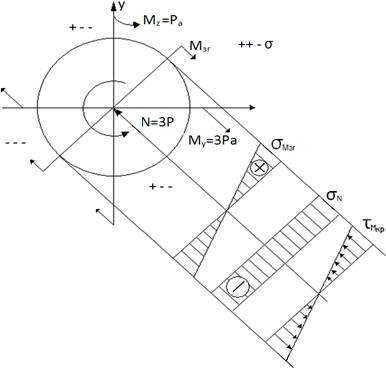
Загальний випадок складного опору
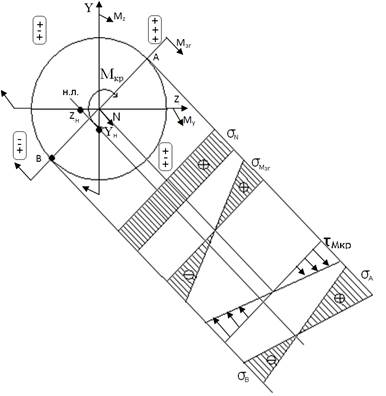
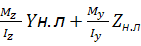 +
+ 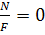
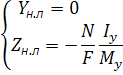
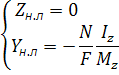
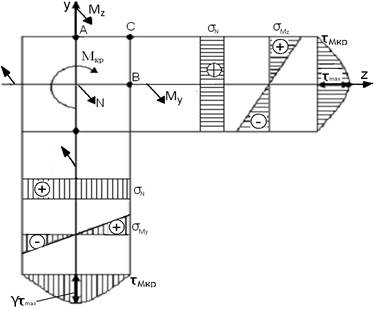 Небезпечний переріз визначається по епюрам внутрішніх силових факторів -
Небезпечний переріз визначається по епюрам внутрішніх силових факторів - 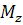 ,
, 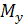 ,
, 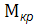 , N.Небезпечні точки - по епюрам напружень від цих зусиль.
, N.Небезпечні точки - по епюрам напружень від цих зусиль.
Круглий переріз
Небезпечна точка А знаходиться у площині дій сумарного згинального моменту. Матеріал знаходиться у плоско-напруженому стані, умова міцності записується за теоріями міцності.
Наприклад,по III теорії:
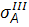 =
= 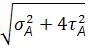 =
= 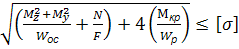
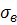 =
= 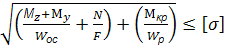
Знаходимо небезпечну точку в перерізі:
Лекція №Розрахунок тонкостінних осесиметричних оболонок
До осесиметричних тонких оболонок можна віднести цистерни, резервуари, повітряні й газові балони, котли, частини корпусів турбін і реактивних двигунів.
Тонкостінною осесиметричною оболонкою називається оболонка, що має форму тіла обертання, відношення товщини стінки якої до найменшого радіуса кривизни не перевищує 0,05.
Якщо така оболонка навантажена осеситмерично (тобто навантаження симетричне відносно осі оболонки), то задача зветься осесиметричною, і в цьому разі в усіх перерізах, утворених площинами, що проходять крізь вісь симетрії, і в перпендикулярних до них перерізах 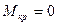 ;
; 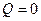 .Якщо оболонка немає різних переходів та жорстких защемлень і не навантажена зосередженими силами та моментами, то згин відсутній (
.Якщо оболонка немає різних переходів та жорстких защемлень і не навантажена зосередженими силами та моментами, то згин відсутній ( 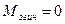 ), напруження розтягу, що виникають можна прийняти сталими по товщині, тобто оболонка знаходиться у безмоментному стані і для розрахунку розраховується безмоментна теорія оболонок.
), напруження розтягу, що виникають можна прийняти сталими по товщині, тобто оболонка знаходиться у безмоментному стані і для розрахунку розраховується безмоментна теорія оболонок.
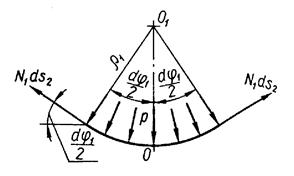
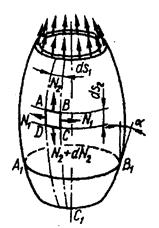 Розглянемо резервуар, що є осесиметричною оболонкою у безмоментному стані під внутрішнім тиском. В стінках оболонки виникають тільки напруження розтягу, розподілення яких по товщині можна прийняти сталими. Виділимо з розглядуваної оболонки малий елемент двома близькими осьовими перерізами та двома ортогональними до них перерізами. Розміри елемента по меридіану
Розглянемо резервуар, що є осесиметричною оболонкою у безмоментному стані під внутрішнім тиском. В стінках оболонки виникають тільки напруження розтягу, розподілення яких по товщині можна прийняти сталими. Виділимо з розглядуваної оболонки малий елемент двома близькими осьовими перерізами та двома ортогональними до них перерізами. Розміри елемента по меридіану 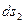 , а по перпендикулярному до нього напряму
, а по перпендикулярному до нього напряму 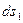 .
.
Радіуси кривизни медіана (перпендикулярного до нього перерізу) позначимо 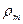 і
і 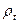 . Товщину стінки позначимо через
. Товщину стінки позначимо через 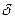 . На гранях виділеного елемента внаслідок симетрії діють тільки нормальні напруження
. На гранях виділеного елемента внаслідок симетрії діють тільки нормальні напруження 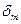 - у меридіальному;
- у меридіальному; 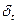 - у широтному напряму. У даному випадку резервуар знаходиться під внутрішнім тиском, і напруженням розтягування.
- у широтному напряму. У даному випадку резервуар знаходиться під внутрішнім тиском, і напруженням розтягування.
Виділимо елемент ABCD і запишемо умови рівноваги.
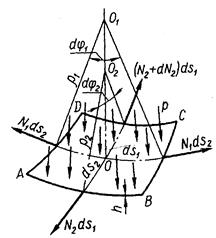
р – внутрішній тиск.
У гранях АВ та CD напруження можуть відрізнятися на величину 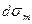 , навантаження на гранях AD і ВС внаслідок осьової симетрії однакові
, навантаження на гранях AD і ВС внаслідок осьової симетрії однакові
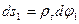
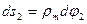
Запишемо умови рівноваги елемента, прирівнюючи до нуля суму проекцій усіх сил на нормаль ОО1 до елемента.
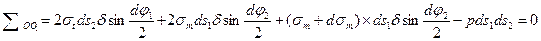 (2)
(2)
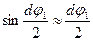 і
і 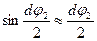 , так як кути малі.
, так як кути малі.
Також враховуючи рівняння (1)
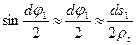 ;
; 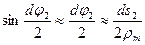
Доданок 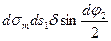 має більш високий порядок малості і ним можна знехтувати. Тоді рівняння (2) прийме вигляд:
має більш високий порядок малості і ним можна знехтувати. Тоді рівняння (2) прийме вигляд:
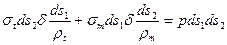 (4)
(4)
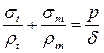 (5) – рівняння Лапласа
(5) – рівняння Лапласа
Це основне рівняння, що зв’язує напруження 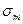 для тонкостінних оболонок обертання, яке зветься рівняння Лапласа.
для тонкостінних оболонок обертання, яке зветься рівняння Лапласа. 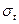 – зветься коловим (широтним, кільцевим) нормальним напруженням;
– зветься коловим (широтним, кільцевим) нормальним напруженням; 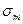 – меридіанним нормальним напруженням.
– меридіанним нормальним напруженням.
Тоді для розрахунку на міцність слід користуватися відповідною теорією міцності. Наприклад, за IV теорія міцності:
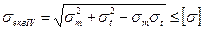 (6)
(6)
Деформації відповідно у широтному і меридіальному напрямку визначаються:
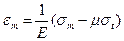 ;
; 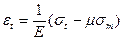 (7)
(7)
Розглянемо приклад розрахунку безмоментних оболонок.
1.Сферична посудина під внутрішнім тиском.
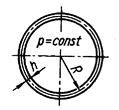
Внаслідок центральної симетрії 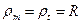 ;
; 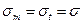
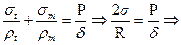
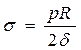
Таким чином: 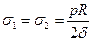
Умова міцності: 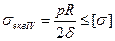
Циліндричний сосуд(посудина) під дією внутрішнього тиску р
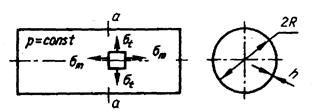
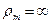 ;
; 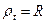
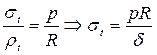
Для визначення 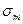 проведемо переріз до осі циліндра, і розглянемо рівновагу будь-якої з частин циліндра:
проведемо переріз до осі циліндра, і розглянемо рівновагу будь-якої з частин циліндра:
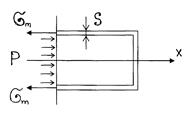
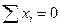
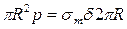
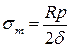
Елемент, що виділяємо з циліндричної оболонки знаходиться у плоско-напруженому стані:
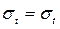 ;
; 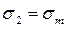 ;
; 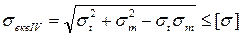
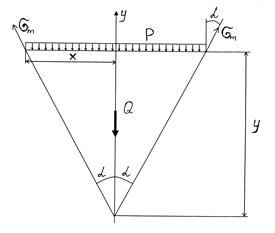
3.Конічна посудина під гідростатичним тиском
Закріплена по верхньому краю:
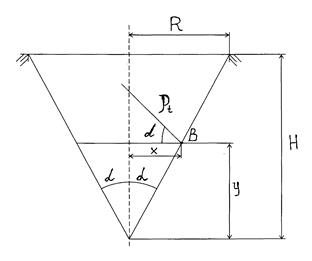
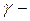 питома вага рідини
питома вага рідини
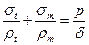
Тут 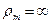
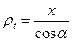 ;
; 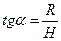
У довільній точці В на рівні у:
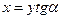 ; р=
; р= 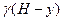
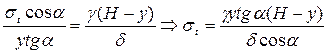
 Для визначення
Для визначення 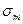 складемо рівняння відсіченої частини оболонки:
складемо рівняння відсіченої частини оболонки:
Вага рідини: 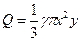
Тиск 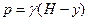
Рівняння рівноваги:
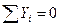
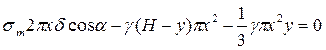
Підставимо 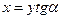 , отримаємо:
, отримаємо:
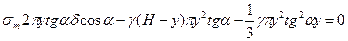
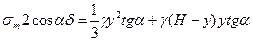
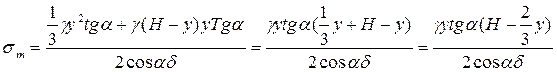
Визначимо небезпечну точку, тобто треба знайти 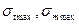 :
:
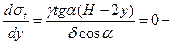 найдемо екстремум функції
найдемо екстремум функції 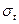
Н-2у=0 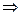
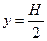
Тобто 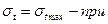
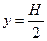
Знайдемо 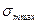
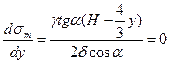 звідки
звідки 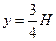 ;
;
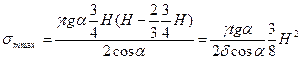
Як видно максимуми напружень 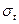 та
та 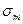 розташовані в різних перерізах по висоті посудини, отже умови міцності треба записати для двох точок (при
розташовані в різних перерізах по висоті посудини, отже умови міцності треба записати для двох точок (при 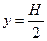 та при
та при 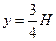 , тобто найбільш небезпечну). Епюри напружень мають вигляд:
, тобто найбільш небезпечну). Епюри напружень мають вигляд:
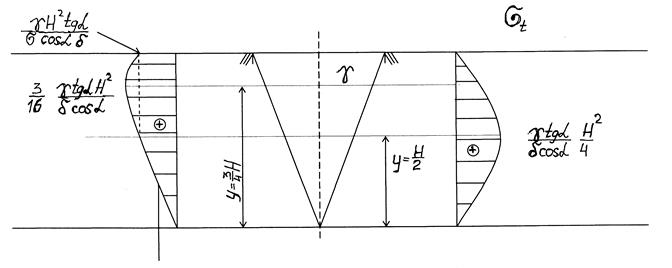
Найбільш небезпечна точка при 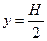 (знайшли
(знайшли 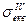 при
при 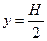 та при
та при 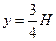 і порівняли їх і визначили небезпечну точку).
і порівняли їх і визначили небезпечну точку).
Дата добавления: 2017-01-13; просмотров: 1391;

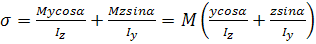 (2)
(2)