Лекція № Пружні коливання
Розглянемо механічні коливання, які дуже часто виникають при експлуатації елементів машин у енергетичних галузях.
Якщо пружне тіло буде виведене з положення рівноваги якою-небудь сторонньою причиною, то сила пружності цього тіла в новому положенні вже не зрівноважиться навантаженням, і виникнуть коливання. Розрізняють два класи коливальних процесів:
1. періодичні
2. неперіодичні
Періодичним – називається такий процес, при якому коливна величина взята у
Будь-який момент часу, через певний відрізок часу Т (період) повторюється
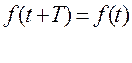
Решта функцій, які не задовольняють зазначеній умові називаються неперіодичними.
Класифікуючи механічні коливання за іншими ознаками, розрізняють такі типи коливань:
1. власні
2. вимушені
3. параметричні
4. автоколивання
Власними (вільними) називаються коливання, які виникають в ізольованій системі внаслідок зовнішнього збудження, що спричинює початкові відхилення від положення рівноваги, і тривають потім завдяки внутрішнім пружнім силам.
Вимушеними називають коливання пружної системи, які відбуваються при дії на систему ( протягом усього періоду коливань) заданих зовнішніх збуджувальних сил, що періодично змінюються і діють безперервно.
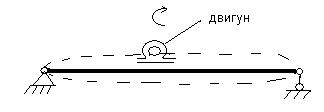
Параметричними називаються коливання пружної системи, в процесі яких періодично змінюються фізичні параметри системи, тобто величини, що характеризують масу системи або її жорсткість.
Автоколиваннями пружної системи називають незатухаючі коливання, що підтримуються такими зовнішніми силами, характер дій яких визначається самими коливальними процесами механічної системи.
Приклад автоколивань: флатер.
За характером деформації пружних елементів конструкцій коливання бувають: повздовжні, поперечні, крутильні, коливання змішаного типу – змінно-крутильними і т.п.
Гармонічні коливання це коливання за знаком синуса чи косинуса.
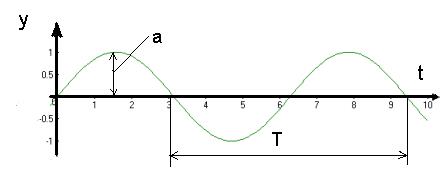
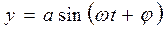
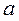 - амплітуда (м);
- амплітуда (м); 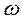 - кутова, колова, власна частота (
- кутова, колова, власна частота ( 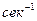 );
); 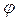 - початкова фаза.
- початкова фаза.
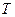 – період коливань
– період коливань
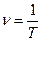 – технічна частота, або секундна частота, тобто число коливань за одну секунду. Одиниці вимірювання секундної частоти (Гц)
– технічна частота, або секундна частота, тобто число коливань за одну секунду. Одиниці вимірювання секундної частоти (Гц)
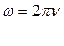
Кругова частота – це кількість коливань за 2π сек.
Власні гармонічні коливання пружної системи з одним ступенем вільності.
 Повне переміщення
Повне переміщення
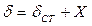
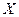 – відхилення від положення рівноваги
– відхилення від положення рівноваги
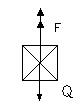
 – статичне подовження пружини F – сила пружності Q – сила ваги
– статичне подовження пружини F – сила пружності Q – сила ваги 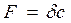 ;
;
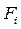 - сила інерції
- сила інерції
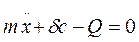
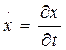 - похідна ;
- похідна ;
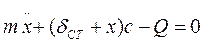
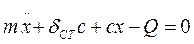
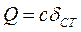
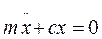
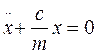
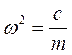
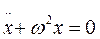 - рівняння власних коливань
- рівняння власних коливань
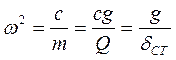
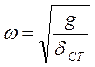
Рівняння має розв’язок
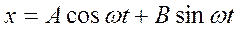
А, В – сталі інтегрування, що залежать від нових умов
Початкові умови: 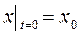 ;
; 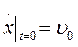
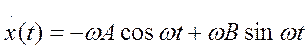
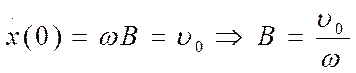
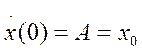
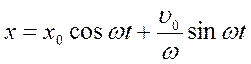
Якщо представити : 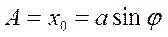
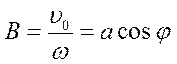
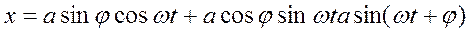 ,
,
де 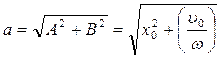
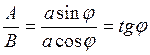
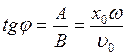
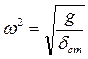
T = 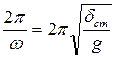
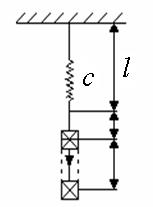
Приклад. Визначити власну частоту вантажу Q, що підвішений до кінця стержня.

l

Sст = 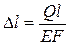
C – жорсткість стержня
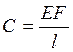
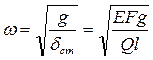
Приведена вище теорія справедлива для поперечних та крутильних коливань.






 H
H

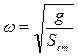
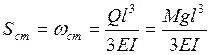
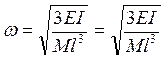
При крутильних коливаннях

Позначимо крутильну жорсткість стержня через
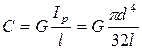
l


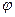
D
l – довжина вала, кут закручування 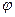
Рівняння коливання таке:
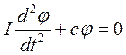
I – момент інерції маси диска відносно осі стержня, перпендикулярно до площини диску. Для круглого диска товщини діаметром D:
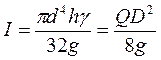
Q – вага диска 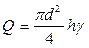
Позначив 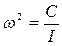 , рівняння коливань буде:
, рівняння коливань буде:
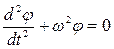
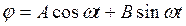 ;
; 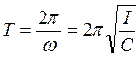
Вимушені коливання пружних систем з одним ступенем вільності:
Якщо вважати, що крім постійної ваги вантажу Q на нього діє періодична сила

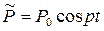 , то буде випадок вимушених коливань . P0 – амплітуда вимушеної сили ; р – частота вимушеної сили;
, то буде випадок вимушених коливань . P0 – амплітуда вимушеної сили ; р – частота вимушеної сили;
Рівняння вимушених коливань








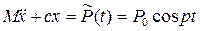

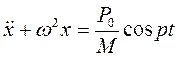

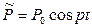
Розв’язок цього рівняння можна отримати як суму рівнянь загального однорідного рівняння та частинного неоднорідного рівняння
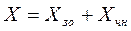
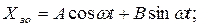
Рівняння частинного неоднорідного рівняння відбираємо по виду правої частини
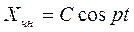
Де А, В, С – сталі, які підлягають визначенню.
Підставляємо частинного розв’язок у диференціальне рівняння
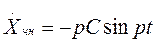 ;
; 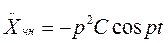
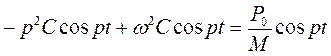

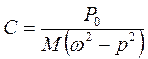
Тоді загальний розв’язок рівняння
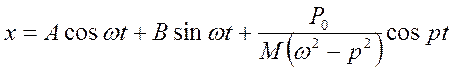
Сталі А та В визначаються з початкових умов
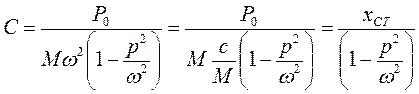
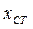 - статичне переміщення від сили
- статичне переміщення від сили 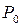
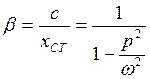 - коефіцієнт наростання коливань
- коефіцієнт наростання коливань
Розсіяння енергії при власних коливаннях системи з 1 ступенем вільності з урахуванням в’язкого тертя.
Розглянемо коливання системи з одним ступенем вільності з урахуванням в’язкого тертя:



Рівняння коливань:
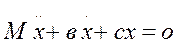
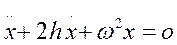 (*)
(*)
де 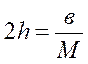 , в – коефіцієнт в’язкого тертя
, в – коефіцієнт в’язкого тертя
Загальний розв’язок рівняння (*) має вигляд:
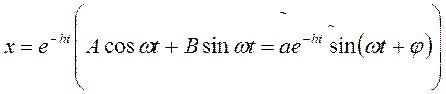 (**)
(**)
де 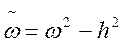
Розглядаючи рішення (**) можна побачити, що амплітуда коливань з часом
Зменшується. Сталі Ата В знаходимо , як і раніше з початкових умов . Графік руху буде такий :
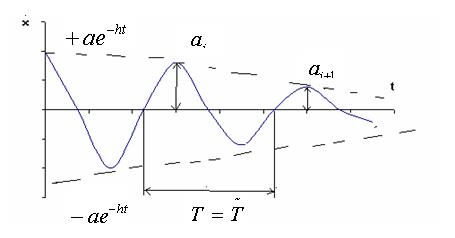
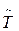 - період коливань системи з тертям
- період коливань системи з тертям
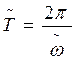
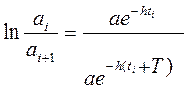 =ln e
=ln e 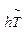 = h
= h 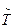 = const
= const
Вимушені коливання з урахуванням енергії.
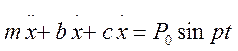

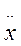 +2h
+2h 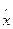 +
+ 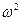 x=
x= 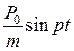
Загальне рішення
x= 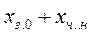 A, В - з початкових умов
A, В - з початкових умов

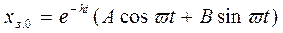 ;
; 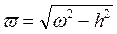
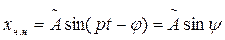
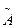 - амплітуда вимушених коливань
- амплітуда вимушених коливань
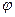 - початкова фаза вимушених коливань
- початкова фаза вимушених коливань
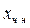 =p
=p 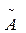 cos
cos 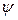
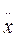 =-p
=-p 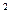
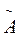 sin
sin 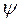
-p 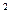
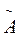 sin
sin 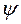 +2hp
+2hp 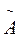 cos
cos 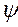 +
+ 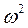
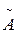 sin
sin 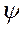 =
= 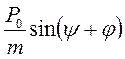
-p 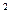
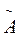 sin
sin 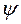 +2hp
+2hp 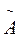 cos
cos 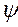 +
+ 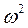
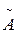 sin
sin 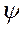 =
= 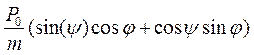
Прирівняємо коефіцієнти при sin 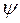 і cos
і cos 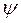
-p 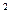
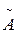 +
+ 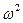
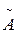 =
= 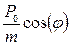
 *
*
2hp  =
= 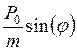
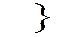 *
*
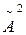 (
( 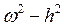 )
) 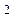
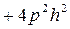
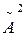 =
= 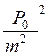 (
( 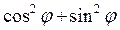 )
)
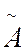 =
= 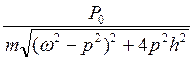 - амплітуда
- амплітуда
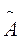 =
= 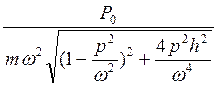 =
= 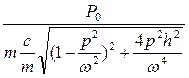 =
= 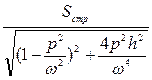
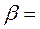
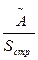 =
= 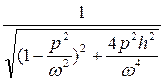
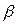 - коефіцієнт наростання амплітуди коливань
- коефіцієнт наростання амплітуди коливань
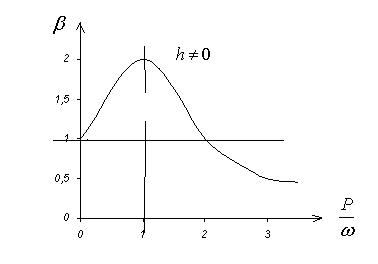
кут зсуву фаз :
tg 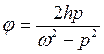 - отримали розділивши друге рівняння(*) на перше
- отримали розділивши друге рівняння(*) на перше
Напруження що виникає при коливаннях
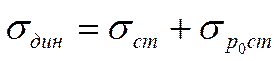 
|
Лекція № Розрахунки на міцність елементів теплоенергетичного обладнання під дією повторно-змінних навантажень
Тема 1: Поняття про втому матеріалів
Значна кількість деталей машин працює в таких умовах, коли напруження, які виникають у них періодично змінюється за значенням або за значенням та знаком. Якщо елементи конструкції багаторазово піддавати змінному навантаженню певного рівня, то після деякої кількості змін напружень у ньому з’явиться тріщина, яка поступово буде розвиватися.
Руйнування матеріалу під дією повторно – змінних напружень називається руйнуванням від втоми. Втомою матеріалів називають явище руйнування внаслідок поступового нагромадження в них пошкоджень, що приводять до виникнення тріщин при багаторазовому повторенні навантажень. Здатність металів чинити опір руйнуванню при дії повторно – змінних напружень називається опором втоми матеріалу, або витривалістю матеріалу. Максимальне напруження, при якому матеріал здатний чинити опір, не руйнуючись, при будь-якій довільно великій кількості повторень змінних напружень, називається границею витривалості (границею втоми).
Позначаються:
σ-1 – якщо нормальні напруження;
τ-1 – якщо дотичні напруження;
Границя витривалості визначається експериментально. Припускаємо, що напруження є періодичними функціями часу з періодом Т: Р =f(x), де Р – узагальнене напруження воно може бути σ – як нормальні напруження розглянемо і τ – якщо дотичні напруження.
Види циклів напружень:


Симетричний цикл – найбільш небезпечний цикл

Відновний цикл
Бувають ще несиметричні цикли.
Сукупність усіх значень напружень за час одного періоду називають циклом напружень
Основні параметри циклу
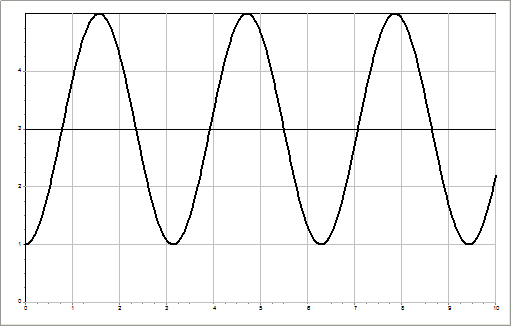
Середнє напруження циклу
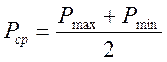
Амплітудне напруження циклу
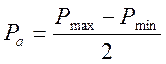
Розмах циклу це подвоєне значення амплітуди.
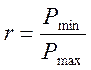
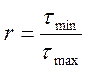
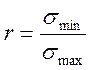
r – називається характеристикою циклу, або коефіцієнтом асиметрії циклу.
r=-1 симетричний цикл це Рсер=0 → Рmax= -Рmin
Від нульовий цикл (пульсуючий Рmin=0)
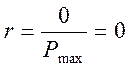
r=1 → Рmax= Рmin це статичне навантаження.
Границею витривалості здобуту при характеристиці циклу r позначають через Рr, тобто σr, τr.
Цикли, що мають однакові характеристики r називають подібними.
Границя витривалості знаходиться експериментально на спеціальних машинах. Найпоширеніші випробування – це згин при симетричному циклі навантаженні. Для випробувань беруть серію з 10-15 однакових відполірованих циліндричних зразків з діаметром робочої частини 5-10 мм.
Робоча частина
 Перший зразок навантажують до значного напруження σ1 – щоб він зруйнувався за порівняно невеликого числа циклів N1. Другий зразок випробують за меншим напруженням він вже простоїть число циклів N2. Потім для наступного зразку знов зменшують напруження, і так до тих пір поки крива не приближаються до асимптоти.
Перший зразок навантажують до значного напруження σ1 – щоб він зруйнувався за порівняно невеликого числа циклів N1. Другий зразок випробують за меншим напруженням він вже простоїть число циклів N2. Потім для наступного зразку знов зменшують напруження, і так до тих пір поки крива не приближаються до асимптоти.
Границя витривалості σ1 максимальним значенням періодичного-змінного напруження, за якого матеріал може необмежено довго чинити опір руйнації.
Якщо сталевий зразок витримав N=107 циклів – це число називається базою випробувань, може витримати необмежене число циклів.
Для кольорових металів границю витривалості визначають на базі випробувань N=108 циклів.

Знаючи тимчасовий опір σ в можна визначити границю витривалості так для сталі:
σ-1р=0,28σв; σ-1зг=0,4σв; τ-1=0,22σв;
Для кольорових металів: σ-1зг=(0,24/0,5)σв
Діаграма граничних напружень
Щоб охарактеризувати опір матеріалів дії напружень що змінюються з різною асиметрією циклу будують діаграму граничних напружень або діаграму Сміта
Починають з симетричного циклу r=-1; σср=0; σ-1max=σ-1; σ-1min= -σ-1 дані випробування партії зразків при певному
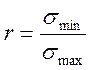
знаходимо
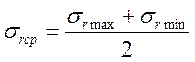
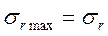
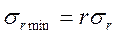
Роблячи так само для інших значень r дістанемо точки М1, N1, M2, N2 і т.д. Сполучимо лініями всі точки, що зображують максимальні та мінімальні граничні напруження циклів. β

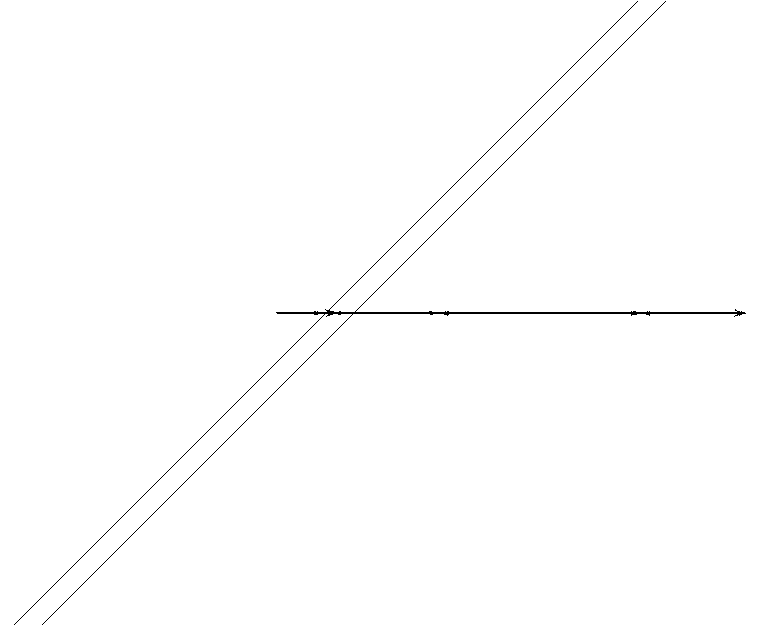
Кратна точка D відповідає циклу при якому σср=σmax=σmin і r=1, тобто сталому навантаженню (статичне навантаження) Ординати точок лінії AD відповідають границям витривалості матеріалу при різних значеннях коефіцієнта асиметрії циклів.
Промені, які проходять крізь початок координат діаграми граничних напружень, є геометричним місцем точок, що характеризують цикли з однаковим коефіцієнтом асиметрії.
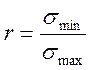
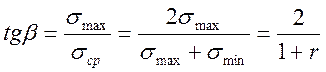
Для визначення границі витривалості матеріалу при даному значені коефіцієнта асиметрії r треба обчислити кут β за формулою
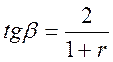
провести промінь між цім кутом до перетину з лінією АD. Ордината точки перетину дорівнює σr .
 Діаграму граничних напружень можна будувати також у координатах σа- σср.
Діаграму граничних напружень можна будувати також у координатах σа- σср.
На цій діаграмі пряма, проведена з початку координат під деяким кутом також характеризує цикли з однаковою асиметрією.
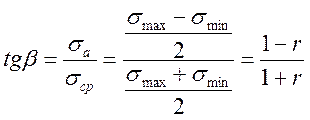
1. Вплив конструктивно-технологічних факторів на границю витривалості
Найбільш важливим фактором, що знижує границю витривалості, є концентрація напружень, спричинена різкою зміною перерізу. Концентраторами напружень є отвори в деталі, нарізки на поверхні шпона канавки.
Кількісною характеристикою концентрації напружень є теоретичний коефіцієнт напруження ασ, який дорівнює відвантаженню найбільшого місцевого напруження σmax до номінального напруження σ, тобто
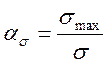
При розтягу стисканні
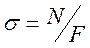
При згині
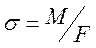
При крученні
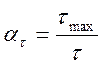
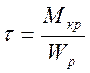
Дійну оцінку впливу концентратора напружень при змінних навантаженнях порівнявши границі витривалості, визначені з дослідів над гладенькими зразками (σ-1) і над зразками з досліджуваним концентратором (σ-1)d за симетричного циклу. Відношення цих величин називають ефективним коефіцієнтом концентрації напружень Кσ або Кτ
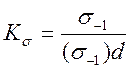
Ефективні коефіцієнти концентрації напружень Кσ менші за ασ. Кількісно цю різницю характеризує коефіцієнт чутливості матеріалу до концентрації напружень:
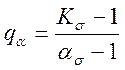
Тоді
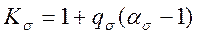
2. Вплив розмірів (масштабний фактор)
З дослідів встановлено, що границя витривалості залежить від абсолютних розмірів поперечного перерізу зразка: із збільшенням розмірів границя витривалості зменшується. Ця закономірність дістала назву масштабного фактора. Вона пояснюється тим, що із збільшенням об’єму матеріалу збільшується ймовірність неоднорідності його структури. Вплив розмірів деталі на границю витривалості враховують масштабним коефіцієнтом Eσ
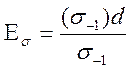
це відношення границі витривалості деталі розміром d до границі витривалості еталонного зразка похожої форми, який має стандартні розміри d=7…10мм.
Масштабний коефіцієнт визначають за допомогою графіків, наданих у довідковій літературі.
3. Вплив стану поверхні.
Поверхня деталі завжди має дефекти, пов’язані з якість механічної обробки, а також з корозією внаслідок впливу оточуючого середовища. Тому тріщини від втоми матеріалу починається з поверхні, а погана якість останньої приводить до зниження опору втомленості. Це пояснюється тим, що риски та подряпини на поверхні деталі є концентратором напружень. Вплив стану поверхні деталі на витривалість оцінюють коефіцієнтом якості поверхні βσ, який дорівнює відношенню границі витривалості (σ-1)n зразка із заданим станом поверхні, до границі витривалості σ-1 зразка з полірованою поверхнею:
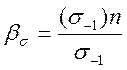
Значення βσ залежить від стану поверхні знаходять за допомогою наведених в довідковій літературі графіків и таблиць.
Запишемо коефіцієнт концентрації деталі.
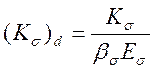
Лекція № Вплив різних факторів
на механічні властивості матеріалів
Механічні характеристики матеріалів залежать від багатьох факторів.
На властивості металів та сплавів істотно впливають хімічний склад, їх термічна та хімічна обробка, умови експлуатації—температура, середовище, характер навантаження тощо.
Останнім часом розвиваються нові види техніки: реактивна авіація, ракетна техніка, атомна енергетика тощо. Матеріали, що застосовуються у нерівних конструкціях нової техніки, зазнають дії високих температур, великих швидкостей навантажування, агресивних рідких та газоподібних середовищ, радіоактивних, особливо нейтронних, проникних випромінювань. Для роботи в цих умовах створюють нові спеціальні сплави та композиційні матеріали [1].
Нижче розглядається вплив деяких факторів на механічні характеристики найбільш важливих у машинобудуванні матеріалів — сталі, чавуну, алюмінію, різних сплавів.
 |
12.1. Вплив високих температур. [1]Багато деталей сучасних машин (наприклад, парових та газових турбін, реактивних двигунів, атомних реакторів та ін.) працюють при високих температурах, що досягають 800...1000 °С. Випробування показали, що всі механічні характеристики металів істотно змінюються залежно від температури.
На рис. 12.1 наведено діаграми напружень вуглецевої сталі при різних температурах, а на рис. 12.2 — графіки залежності від температури границі текучості, тимчасового опору й відносного подовження при розтяганні. В інтервалі температур 150...250 °С тимчасовий опір досягає найбільшого значення, а відносне подовження після розриву — найменшого; сталь, як кажуть, стає сильно ламкою. За більш високих температур міцність вуглецевої сталі швидко зменшується, тому при температурах, вищих за 350...400 °С, таку сталь не застосовують.
З підвищенням температури також істотно зменшується модуль пружності Е (рис. 12.3), а коефіцієнт Пуассона дещо збільшується. Так, при зростанні температури від кімнатної до 500 °С коефіцієнт Пуассона збільшується від 0,28 до 0,33.
 Вуглецеві сталі при високих температурах дуже окислюються, на їхній поверхні утворюється окалина. У зв'язку з цим застосовують спеціальні жаростійкі та жароміцні сталі, які містять у собі різні легуючі добавки. Жаростійкістю називають властивість матеріалу протистояти хімічному руйнуванню поверхні при високих температурах, а жароміцністю — здатність зберігати при високих температурах механічні властивості. Останнім часом створено спеціальні сплави, а також металокерамічні матеріали, що надійно працюють при температурах до 100 °С.
Вуглецеві сталі при високих температурах дуже окислюються, на їхній поверхні утворюється окалина. У зв'язку з цим застосовують спеціальні жаростійкі та жароміцні сталі, які містять у собі різні легуючі добавки. Жаростійкістю називають властивість матеріалу протистояти хімічному руйнуванню поверхні при високих температурах, а жароміцністю — здатність зберігати при високих температурах механічні властивості. Останнім часом створено спеціальні сплави, а також металокерамічні матеріали, що надійно працюють при температурах до 100 °С.
 |
12.2. Повзучість [1]. При високих температурах істотне значення має явище повзучості матеріалів (крип), яке характеризується зростанням пластичної деформації з часом при постійному напруженні, що не спричинює пластичних деформацій під час короткочасної дії навантаження. Залежно від напруження та температури деформація, що виникає внаслідок повзучості, може або припинитися, або продовжуватися до руйнування матеріалу.
На рис. 12.4, а наведено криві повзучості сталі при постійній температурі для різних напружень  , а на рис. 12.4, б — криві повзучості при постійному напруженні, але різних температурах, причому Т1 < Т2 < Т3 < Т4 < Т5. Як видно із порівняння графіків, збільшення напруження при постійній температурі й підвищення температури при постійному напруженні однаково впливають на повзучість матеріалу, а саме — швидкість повзучості збільшується.
, а на рис. 12.4, б — криві повзучості при постійному напруженні, але різних температурах, причому Т1 < Т2 < Т3 < Т4 < Т5. Як видно із порівняння графіків, збільшення напруження при постійній температурі й підвищення температури при постійному напруженні однаково впливають на повзучість матеріалу, а саме — швидкість повзучості збільшується.
Окремі відрізки кривих рис. 12.4 характеризують різні швидкості наростання деформації. Розглянемо, наприклад, криву 4. Вертикальний відрізок Оа відображує подовження, здобуте відразу після навантажування. Відрізок аb — це відрізок неусталеної повзучості, оскільки швидкість її тут з часом зменшується. Прямолінійний відрізок bс називається відрізком усталеної повзучості, що характеризується її постійною швидкістю. Відрізок сd характеризує зростання швидкості повзучості, що закінчується руйнуванням зразка (точка d).
Решта кривих повзучості відрізняється від кривої 4 тим, що в них немає того чи іншого відрізка. Так, криві 1, 2 та 3 зображують випадки, коли повзучість не спричинює руйнування (на них немає відрізка сd). Крива 5 не має відрізка усталеної повзучості (точки b та с збігаються). Ця крива відповідає випадку, коли період неусталеної повзучості заміняється відразу періодом із зростаючою її швидкістю, який закінчується руйнуванням. Межа між цими двома періодами визначається точкою перегину b.
Границею повзучості називається найбільше напруження, при якому швидкість або деформація повзучості при даній температурі за певний проміжок часу не перевищує встановленого значення (наприклад, швидкості 0,0001 %/год. або деформації 1 % за 10 000 год.).
Якщо границю повзучості визначають за деформацією, то позначають її літерою 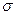 з трьома числовими індексами: двома нижніми й одним верхнім. Перший нижній індекс відображує задане подовження (сумарне або залишкове), %; другий нижній індекс — заданий час випробування, год.; верхній індекс — температуру, °С. Наприклад, запис
з трьома числовими індексами: двома нижніми й одним верхнім. Перший нижній індекс відображує задане подовження (сумарне або залишкове), %; другий нижній індекс — заданий час випробування, год.; верхній індекс — температуру, °С. Наприклад, запис 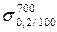 означає границю повзучості при допуску на деформацію 0,2% за 100 год. випробування при температурі 700 °С. При цьому треба додатково зазначити, за сумарною чи залишковою деформацією визначалася границя повзучості.
означає границю повзучості при допуску на деформацію 0,2% за 100 год. випробування при температурі 700 °С. При цьому треба додатково зазначити, за сумарною чи залишковою деформацією визначалася границя повзучості.
Якщо границя повзучості визначається за швидкістю повзучості, то її потрібно позначати літерою 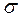 з двома числовими індексами: одним верхнім й одним нижнім. Нижній індекс відображує задану швидкість повзучості, %/год; верхній — температуру випробування, °С. Наприклад,
з двома числовими індексами: одним верхнім й одним нижнім. Нижній індекс відображує задану швидкість повзучості, %/год; верхній — температуру випробування, °С. Наприклад, 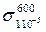 - це границя повзучості при швидкості її
- це границя повзучості при швидкості її 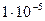 %/год при температурі 600 °С. При цьому треба додатково зазначити час випробування, протягом якого було досягнуто задану швидкість повзучості.
%/год при температурі 600 °С. При цьому треба додатково зазначити час випробування, протягом якого було досягнуто задану швидкість повзучості.
Деталі, що працюють при високих температурах, розраховують на повзучість спеціальними методами з використанням експериментальних даних, які характеризують повзучість матеріалу. Метою таких розрахунків є визначення границь повзучості.
За результатами експериментального визначення швидкості повзучості 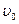 при розтяганні зразків будують графіки в логарифмічних координатах lg
при розтяганні зразків будують графіки в логарифмічних координатах lg 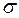 ~lg
~lg 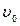 . Експериментальні точки добре групуються навколо деякої прямої (рис. 12.5, а).
. Експериментальні точки добре групуються навколо деякої прямої (рис. 12.5, а).
Зазначимо, що в деяких матеріалах (свинець, бетон, високо-полімерні матеріали тощо) повзучість спостерігається й при нормальній температурі.
 |
12.3. Тривала міцність [1].У разі високої температури й довгочасної дії навантаження відбувається руйнування матеріалу при напруженні, яке менше за тимчасовий опір матеріалу при даній температурі. У зв'язку з цим виникає потреба визначити тривалу міцність матеріалів.
Границею тривалої міцності називається напруження, що спричинює розрив зразка після заданого строку безперервної дії цього напруження при певній температурі. Позначається границя тривалої міцності літерою σ з двома числовими індексами. Верхній індекс вказує температуру випробування, °С, нижній — задану тривалість випробування до руйнування, год. Останню можна позначити кількістю годин або цифрою 10 з показником степеня. Наприклад, 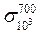 або
або 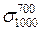 —границя тривалої міцності за 1000 год випробування при температурі 700 °С.
—границя тривалої міцності за 1000 год випробування при температурі 700 °С.
Випробування на тривалу міцність полягає в тому, що зразки піддають різним напруженням при певній температурі і дізнаються про час до їх розриву. Результати подають у вигляді графіка (рис. 12.5, б). Маючи криву тривалої міцності матеріалу, можна визначити руйнівне напруження за заданим строком роботи деталі при заданій температурі; або за заданим напруженням можна визначити час до руйнування. Наприклад, деталь, виготовлена з матеріалу, для якого криву тривалої міцності зображено на рис. 12.5, б, при напруженні З0 МПа та температурі 500°С зруйнується через 2550 год.
Результати експериментального визначення тривалої міцності зручно подавати у логарифмічних координатах lg 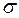 ~lgt, де вони досить добре апроксимуються прямими (рис. 12.5, а).
~lgt, де вони досить добре апроксимуються прямими (рис. 12.5, а).
Зазначимо, що чим менше руйнівне напруження, а отже, більший час розриву, тим менше відносне подовження при розриві, тобто матеріал стає більш крихким. Для низки матеріалів (наприклад, для високо-полімерів) зазначений ефект виявляється і при кімнатній температурі.
12.4. Релаксація напружень [1].Релаксацією напруженьназивається зменшення їх з часом унаслідок повзучості в навантаженій деталі при незмінній її повній деформації. У більшості металів релаксація помітна лише при високих температурах (рис. 12.6). Для ілюстрації цього явища наведемо такі приклади.
 |
Між розведеними кінцями розрізаного сталевого кільця вставимо пластинку (рис. 12.7). Унаслідок деформації кільця в ньому виникнуть напруження, і кінці кільця, намагаючись зблизитися, з великою силою стиснуть пластинку. Якщо це з'єднання витримати деякий час при високій температурі, то в кільці відбудеться релаксація напружень, сила затискання пластинки зменшиться і її можна буде легко вийняти.
Відомо, що початкове затягування болтів, які працюють при високій температурі, з часом слабшає, і це спричинює потребу підтягувати їх.
12.5. Вплив низьких температур [1]. Намеханічні властивості деяких матеріалів істотно впливають низькі температури. Це виявляється в тому, що матеріали, пластичні при нормальній температурі, стають крихкими при низьких температурах. Такі матеріали називають холодноламкими.
 Холодноламкість характерна для металів, що мають кристалічні ґратки у вигляді об’ємноцентрованого куба або гексагональні. До них належать більшість чорних металів, зокрема сталі, а також цинкові сплави. Виявляється холодноламкість як при статичній дії навантаження, так і при динамічній. Як приклад на рис. 12.8 наведено графіки зміни границі текучості, тимчасового опору, відносних подовження і звуження при статичних випробуваннях вуглецевої сталі при низьких температурах.
Холодноламкість характерна для металів, що мають кристалічні ґратки у вигляді об’ємноцентрованого куба або гексагональні. До них належать більшість чорних металів, зокрема сталі, а також цинкові сплави. Виявляється холодноламкість як при статичній дії навантаження, так і при динамічній. Як приклад на рис. 12.8 наведено графіки зміни границі текучості, тимчасового опору, відносних подовження і звуження при статичних випробуваннях вуглецевої сталі при низьких температурах.
Метали, що кристалізуються в системі куба з центрованими гранями (мідь, алюміній, нікель, срібло, золото тощо), не виявляють холодноламкості ні за якого зниження температури. Наприклад, алюміній при температурі рідкого азоту (-196°С) збільшує міцність приблизно в 2 рази, одночасно збільшуючи відносне подовження в 4 рази. Аналогічно поводять себе мідь та нікель. Багато сплавів алюмінію, міді, а також деякі сталі не виявляють холодноламкості.
Дата добавления: 2017-01-13; просмотров: 1037;
