Напруження в сталеалюмінієвому проводі від зміни температури

Температурний коефіцієнт лінійного розширення алюмінію майже в два рази більший, ніж сталі. Якби між алюмінієвою та сталевою частинами проводу було відсутнє тертя, то під час нагрівання проводу, наприклад, до температури, яка перевищує температуру його виготовлення (q >q₀ ), алюмінієва частина проводу більше би видовжилася, ніж сталева. А за температури нижчої, ніж температура виготовлення (q <q₀ ), алюмінієва частина проводу стала би коротшою, ніж сталева. В дійсності алюмінієві та стальні дротинки скручені між собою і переміщуватися одні відносно інших не можуть. Провід веде себе як єдине ціле, і видовження алюмінію та сталі під час нагрівання буде однаковим, але при цьому алюмінієва частина проводу буде стискатися, а сталева розтягуватися (рис. 6.1). В алюмінієвій та сталевій частинках проводу виникають температурні напруження.

Якщо б під час нагрівання проводу від q₀ до q алюмінієва і стальна частини розширювалися незалежно, то вони б видовжилися

; ,

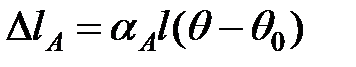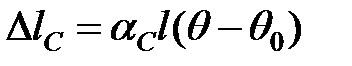(6.8)

де a_А , a_С – коефіцієнти температурного розширення алюмінію і сталі.

В дійсності обидві частини розширюються на

,

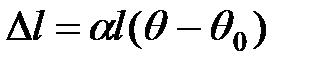(6.9)

де a – фіктивний коефіцієнт температурного розширення проводу.

Дійсне ж видовження алюмінієвої частини проводу буде менше на

,

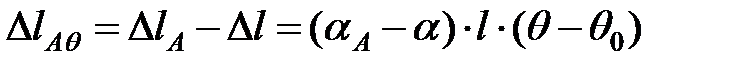(6.10)

а сталевої більше на

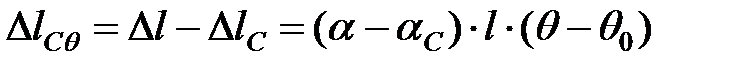
(6.11)

порівняно з незалежним видовженням. На алюмінієву частину проводу діє сила стискання Т_Аq , а на сталеву – сила розтягування Т_Сq . В обох частинах проводу виникають температурні напруження s_Сq і s_Аq . Напруження стискання в алюмінієвій та сталевій частинах проводу можуть бути відповідно визначені за виразами:

; .

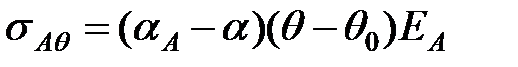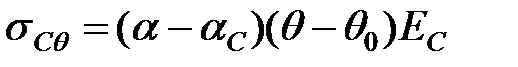(6.12)

Вираз для визначення фіктивного коефіцієнта температурного розширення проводу a можна отримати з умови рівноваги проводу (сила стискання алюмінієвої частини проводу дорівнює силі розтягу його стальної частини)

.

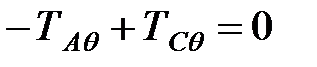(6.13)

З врахуванням формул 13.4, 13.11, 13.12 рівняння буде мати вигляд

.

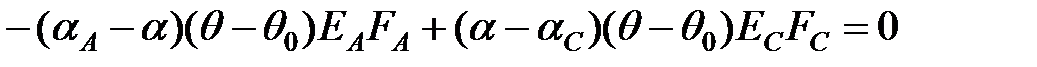(6.14)

Отже, значення фіктивного коефіцієнта температурного розширення проводу можна визначити за виразом

.

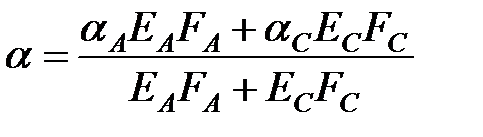(6.15)

Максимальне напруження в сталеалюмінієвому проводі виникає від механічного навантаження та від зміни температури проводу. Результуюче напруження в алюмінієвій частині проводу s_А визначають, як

,

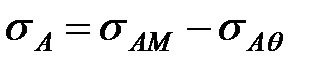(6.16)

де s_АМ , s_Аq - відповідно напруження від механічного навантаження та від зміни температури.

З врахуванням рівняння (6.12) для алюмінієвої частини проводу отримаємо

.

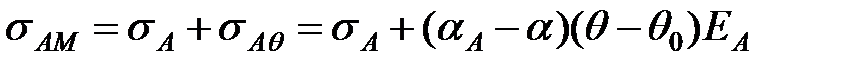(6.17)

Враховуючи рівняння (6.5), фіктивне напруження проводу буде рівне

.

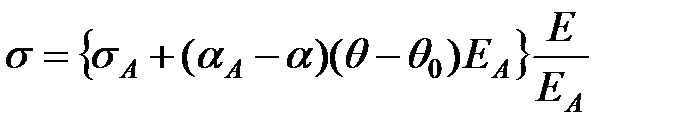(6.18)

Рис. 6.1.

Допустиме напруження в сталеалюмінієвому проводі [s] визначають за виразом

,

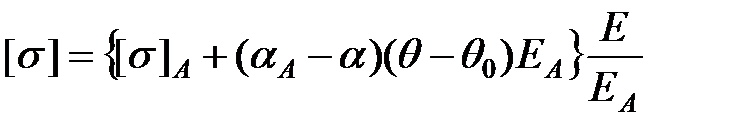(6.19)

де [s]_А , a_А ,Е_А – допустиме напруження, коефіцієнт температурного розширення і модуль пружності алюмінієвої частини проводу; a ,Е визначають з формул 6.7 і 6.15; q , q₀ – відповідно температура проводу та температура виготовлення проводу.

Температурне напруження в алюмінієвій частині проводу s_Аq за умови q >q₀ приводить до збільшення допустимого напруження сталеалюмінієвого проводу [s] у порівнянні з допустимим напруженням алюмінієвого проводу. Напруження за низької температури [s]_qнн не перевищує напруження за найбільшого навантаження [s]_¡нб. Досвід експлуатації повітряних ліній показав, що значення [s]_qнн може бути збільшене до значення [s]_Uнб . 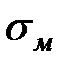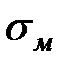На сьогодні прийнято, що [s]_qнн = [s]_Uнб = (0,35¸0,45) , де – межа міцності під час розтягування проводу. За такої умови напруження в алюмінієвій частині проводу не виходить за допустимі межі.