Агрегатные состояния
Состояние данной массы газа определяется тремя величинами (параметрами): давлением p, объемом V и температурой T. Эти величины связаны между собой функциональной зависимостью, которая может быть представлена соотношением f (p, V, T) = 0, называемым уравнением состояния. Уравнение состояния идеального газа выводится из трех законов – Бойля – Мариотта, Гей-Люссака и Авогадро. Реальные газы подчиняются этим законам тем точнее, чем меньше давление и выше температура [1].
Закон Бойля – Мариотта. При постоянной температуре объем данной массы обратно пропорционален давлению. Если V1 и V2 – объемы газа при давлении p1 и p2 соответственно, то
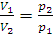
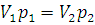 , или
, или 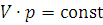 (1.1)
(1.1)
Из закона Бойля – Мариотта вытекает следствие: при постоянной температуре плотность газа ρ пропорционально его давлению:
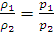 (1.1a)
(1.1a)
Законы Гей-Люссака и Шарля. При постоянном давлении с повышением температуры на 1°С объем данной массы газа увеличивается на 1/273,15 его объема при 0°С:
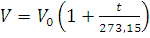 (1.2)
(1.2)
где V – объем газа при температуре t °С, а V0 – объем газа при 0°С.
При замене шкалы Цельсия абсолютной температурной шкалой (шкалой Кельвина), для которой T=273,15+t, этот закон можно сформулировать следующим образом: при постоянном давлении объем данной массы газа пропорционален его абсолютной температуре:
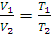 (1.3)
(1.3)
где V1 и V2 – объемы газа при абсолютных температурах T1 и T2
При постоянном объеме зависимость давления данной массы газа от температуры записывается уравнениями, аналогичными (1.2) и (1.3):
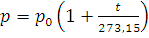 (1.4)
(1.4)
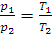 (1.5)
(1.5)
Объединенный закон Бойля – Мариотта – Гей-Люссака выражается уравнением:
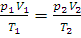 (1.6)
(1.6)
где p1 – давление и V1 – объем данной массы газа при абсолютной температуре T1, p2- давление и V2 – объем той же массы газа при абсолютной температуре T2.
Закон Авогадро: в равных объемах различных газов при одинаковых условиях содержится равное число молекул.
Число молекул (NA) в 1 моль вещества одинаково у всех веществ и равно 6,02·1023 (число Авогадро). Следовательно, количества веществ 1 моль, находящихся в газообразном состоянии при одинаковой температуре и одинаковом давлении, занимают равные объемы. При нормальных условиях (температура 0°С и давление = 1,01325·105 Па) объем 1 моль газа равен 22,414л.
Уравнение состояния идеального газа – уравнение Менделеева – Клайперона для одного моля газа имеет вид:
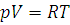 (1.7)
(1.7)
а для любого количества газообразного вещества:
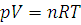 (1.8)
(1.8)
где R – универсальная газовая постоянная, числовое значение которой зависит от единиц измерения других величин. Величина ее выражается в единицах СИ Дж/(моль·К).
Уравнение (1.8) может быть использовано для определения относительной молекулярной массы Мч. Заменяя в нем величину n отношением m/M, где m – масса газа, а M – молярная масса данного газа, и решая его относительно M, получим:
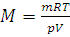 (1.9)
(1.9)
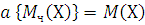
Закон Дальтона: общее давление смеси газов равно сумме парциальных давлений составных частей (компонентов):
 (1.10)
(1.10)
где pоб – общее давление смеси газов, p1, p2, pk – парциальные давления компонентов смеси. Парциальным давлением называется давление каждого компонента, если бы он один занимал объем, равный объему смеси той же температуре.
Уравнения (1.8) и (1.9) применимы к смесям газов, химически не взаимодействующих друг с другом, а также к каждому компоненту смеси. В первом случае n – общее количество вещества компонентов (n=n1+n2+…+nk=∑ni, где i=1, 2, …, k), M – средняя «смешанная» молярная масса, во втором случае n – количество вещества каждого компонента, т.е. n1, n2, …, nk, p – парциальное давление компонента, V – общий объем смеси.
Зависимость между парциальными давлениями и общим выражается уравнениями:
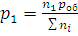 ,
, 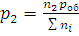 , …,
, …, 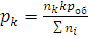 (1.11а)
(1.11а)
Отношения n1/∑ni, n2/∑ni, …, nk/∑ni, называют молярными долями данного компонента. Если молярную долю обозначить через x, то парциальное давление любого i-го компонента смеси (где i = 1, 2, …, k) будет равно:
 (1.11б)
(1.11б)
Таким образом, парциальное давление каждого компонента равно произведению его молярной доли на общее давление смеси.
Для идеальных газов молярная доля x равна объемной доле φ (V1/∑υi, V2/∑υi, …, Vk/∑υi). Если состав смеси выражен в объемных долях (%), то φ'
φ1'/100 = x1, φ2'/100 = x2, …, φk'/100 = xk, (1.12)
Кинетическая теория газов. Основным уравнением кинетической теории газов для 1 моль является уравнение:
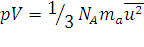 , (1.13)
, (1.13)
где ma – масса молекулы; ū – средняя квадратичная скорость молекул; NA – число молекул в 1 моль. Для любого количества вещества в уравнении вместо NA входит N.
Из основного уравнения кинетической теории газов можно вывести изложенные выше газовые законы и некоторые новые положения.
Сопоставляя уравнения (1.7) и (1.13) получим для 1 моль газа:
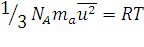 , (1.14)
, (1.14)
1. Отсюда находим среднюю квадратичную скорость молекул:
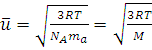 (1.15)
(1.15)
где M = NA·ma – молярная масса газа.
Из этого уравнения следует, что для одного и того же газа средняя квадратичная скорость молекул прямо пропорциональна корню квадратному из абсолютной температуры:
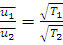 (1.16)
(1.16)
где ū1 – средняя квадратичная скорость при температуре T1, а ū2 –то же самое при T2.
Для различных газов при одинаковой температуре средняя квадратичная скорость молекул обратно пропорциональна корню квадратному из относительных молекулярных масс:
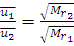 (1.17)
(1.17)
Здесь ū1 и 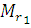 относятся к первому газу, а ū2 и
относятся к первому газу, а ū2 и  - ко второму.
- ко второму.
2. Из уравнения (1.14) находим:
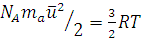 (1.18)
(1.18)
Выражение, стоящее в левой части этого равенства, есть средняя кинетическая энергия поступательного движения молекул идеального газа в количестве вещества 1 моль. Обозначив ее через Е, получим:
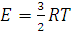 (1.19)
(1.19)
Разделив обе части уравнения (1.18) на NA, найдем, что средняя кинетическая энергия поступательного движения одной молекулы газа равна:
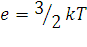 (1.20)
(1.20)
где 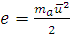 , а
, а 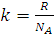 - константа, называемая постоянной Больцмана.
- константа, называемая постоянной Больцмана.
Следовательно, кинетическая энергия идеального газа пропорциональна абсолютной температуре.
Примеры
1.В баллоне емкостью 20 л находится водород под давлением 162·105 Па. Сколько шаров-пилотов можно наполнить водородом, если объем шара равен 200 л и давление в нем должно быть равно 2·105 Па? Водород при этих условиях считать идеальным газом.
Решение. Так как температура и масса газа остаются постоянными, то для решения задачи применим закон Бойля – Мариотта (1.1). После наполнения шаров-пилотов объем водорода (V2) буде равен:
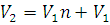
где V3 – объем одного шара; n – число шаров; V1 – объем баллона, в котором водород после наполнения последнего шара находится под давлением 2·105 Па. Заменив в уравнении (1.1) V2 его значением, получим:
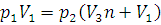
Отсюда
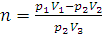
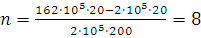
Находим, что водородом можно наполнить восемь шаров-пилотов.
2.При нормальных условиях плотность азота равна 1,25 г/л. Определить плотность газа при 0°С и давлении 5,065·105 Па.
Решение. Требуется определить плотность азота при 0°С и давлении 5,065·105 Па. Из уравнения (I, 1а) находим ρ2 – плотность при давлении p2:
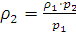 ;
; 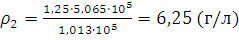
3. При постоянном давлении открытая двухлитровая колба охлаждается от 200 до 0°С. Насколько увеличится масса воздуха в колбе, если плотность воздуха при нормальных условиях равна 1,293 г/л? Изменением объема колбы вследствие охлаждения стекла пренебречь.
Решение. Объем одного и того же количества газа согласно закону Гей-Люссака при 0°С должен быть меньше, чем при 200°С. Если при t2 = 0°С его объем V2 = 2 л, то при t1 = 200°Сон может быть определен из уравнения (1.3):
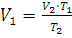 ;
; 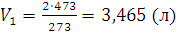
При 0°С масса газа в двухлитровой колбе равна 1,293x2=2,586 (г). При 200°С такую же массу будет иметь 3,465 л. Таким образом, если температура понизится с 200°С до 0°С, то в колбу войдет 3,465-2=1,465 (л) воздуха; соответствующая масса может быть определена из пропорции:
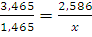 ;
; 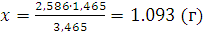
Следовательно, масса газа в колбе увеличится на 1,093 г.
4.Смесь эквивалентных количеств этана и кислорода находится в замкнутом сосуде при температуре 15°С и давлении 1·105 Па. Каково будет давление после взрыва смеси и приведения содержимого сосуда к первоначальной температуре?
Решение. Напишем уравнение реакции горения этана:
2С2Н6 + 7О2 = 4СО2 + 6Н2О
Вода при температуре 15°С будет в жидком состоянии, и при подсчета числа молекул не нужно учитывать образовавшихся молекул воды (так как объем жидкости по сравнению с объемом газа той же массы несоизмеримо мал). Из уравнения следует, что из 9 молекул исходных веществ образовалось 4 молекулы. Так как объем газов и температура остаются постоянными, то с уменьшением числа молекул в 9/4 раза и давление должно уменьшиться в такое же число раз, т.е. оно будет равно: 1·105:9/4=0,4·105 Па.
5.Для хлорирования питьевой воды хлор доставляется в баллонах под давлением. Давление в этих баллонах равно ,722·105 Па при 0°С и 15,47·105 Па при 30°С. Можно ли считать хлор в этих условиях идеальным газом?
Решение. Так как в баллоне объем постоянен, то для идеального газа, как следует из уравнения (I, 5),  - величина постоянная. Вычисляем это отношение для хлора: при 0°С
- величина постоянная. Вычисляем это отношение для хлора: при 0°С 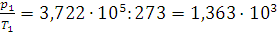 , а при 30°С
, а при 30°С 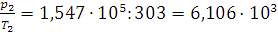 . Оно непостоянно. Следовательно, хлор в этих условиях считать идеальным газом нельзя.
. Оно непостоянно. Следовательно, хлор в этих условиях считать идеальным газом нельзя.
6. При температуре 18°С и давлении 98,64 кПа объем газа равен 2 л. Привести объем газа к равным нормальным условиям.
Решение. Из уравнения (1.6) находим V1 – объем при нормальном давлении 1,013·105 Па и температуре 273 К. Данные задачи переводим в единицы СИ:
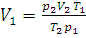 ;
; 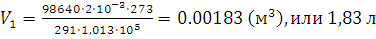
7. Вычислить при нормальных условиях газовую постоянную R, выразив ее в: а) Па·м3/(моль·К); б) Дж/(моль·К).
Решение. Из уравнения (1.7) находим: 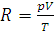 . Подставляем в эту формулу числовые значения: p=1.01325·105Па, Т-273,15 К и Vm=2,2414·10-2 м3 (молярный объем газа):
. Подставляем в эту формулу числовые значения: p=1.01325·105Па, Т-273,15 К и Vm=2,2414·10-2 м3 (молярный объем газа):
а) 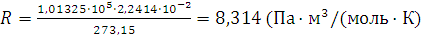 ;
;
б) 8,314 Па·м3/(моль·К) = 8,314 Н/м2 · м3/(моль·К) = 8,314 Дж/(моль·К).
8. Какое количество вещества и какая масса кислорода находится в газометре емкостью 10 л при 20°С и под давлением 100 кПа?
Решение. Решаем уравнение (1.8) относительно n: 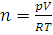 . Данные задач подставляем в уравнение в единицах СИ: R=8,314 Дж/(моль·К), p=1·105 Па, Т=273+20=293 К, V=0,01 м3:
. Данные задач подставляем в уравнение в единицах СИ: R=8,314 Дж/(моль·К), p=1·105 Па, Т=273+20=293 К, V=0,01 м3:
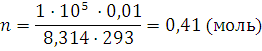
m = nM ; m = 0,41 · 32 = 13,12 (г)
9. По методу В. Майера определялась относительная молекулярная масса этилового эфира. При испарении эфира массой 0,0856 г его пары вытеснили в эвдиометрическую трубку воздух объемом 29,2 мл; высота водяного столба в эвдиометрической трубке 22,5 см, температура воздуха 17°С, атмосферное давление 1005 гПа. Давление насыщенного пара воды при 17°С равно 19,37гПа. Вычислить относительную молекулярную массу эфира и найти относительную ошибку опыта в процентах.
Решение. Давление сухого воздуха, заключенного в эвдиометрической трубке, будет равно:
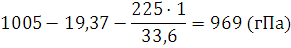
где 1 – значение плотности воды и 13,6 – значение плотности ртути. Подставляем в уравнение (I, 9) соответствующие значения, выразив их в единицах СИ, получаем:
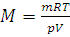 ;
; 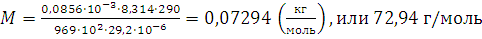
Таким образом, относительная молекулярная масса эфира равна 72,94. Относительная ошибка в процентах равна:
(74,08-72,94)·100:74,08-1,54 %
где 74,08 – табличная величина относительной молекулярной массы эфира.
10. Смешаны водород объемом 3 л и под давлением 2·105 Па с кислородом объемом 2 л под давлением 1·105 Па. Общий объем смеси равен 4 л. Определить парциальные давления газов и общее давление смеси.
Решение. Водород, занимавший объем V1, равный 3 л, при давлении p1 равном 2·105 Па, после смешивания с кислородом распространится в объеме V2, равном 4 л. Парциальное давление водорода , равное p2, находим из закона Бойля – Мариотта (1.1):
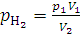 ;
; 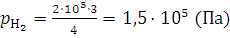 .
.
Парциальное давление кислорода находим аналогичным способом:
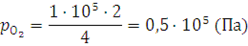
Общее давление p смеси равно: 1,5·105 + 0,5·105 = 2·105 (Па).
11. Смесь из 2 моль азота, 3 моль кислорода и некоторого количества вещества аммиака при 20°С и давлении 4·105 Па занимает объем 40 дм3. Вычислить количество аммиака в смеси и парциальное давление каждого из газов.
Решение. Из уравнения (1.8) находим n – общее количество всех газообразных веществ, составляющих смесь, и подставляем R, равное 8,314 Дж/(моль·К), p = 4·105 Па, V = 4·10-2 м3, T =273+20 = 293 К :
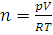 ;
;
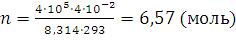
Количество вещества аммиака
n (NH3) = 6,57 – 2 – 3 = 1,57 (моль)
Парциальное давление газов вычисляем по уравнению (1.11а):
p (N2) = 4·105 · 2 : 6,57 = 1,217·105 (Па);
p (O2) = 4·105 · 3 : 6,57 =1,826·105 (Па);
p (NH3) = 4 · 105 · 1,57 : 6,57 =0,956·105 (Па).
12. 0,5 моль водорода и 0,25 моль азота находятся в газометре вместимостью 5 л при 10°С. Вычислить парциальное давление каждого из газов и состав смеси в объемных долях.
Решение. Парциальное давление каждого компонента находим из уравнения (1.8):
 ;
;
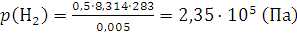
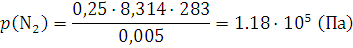
По формуле (1.12) вычисляем содержание водорода и азота в объемных долях:
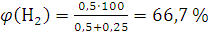 ;
;
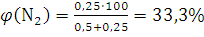
13. Какое давление будет иметь при 0°С кислород объемом 10 л и количеством вещества 0,25 моль? Средняя квадратичная скорость молекул кислорода при этой температуре равна 461 м/с.
Решение. Из формулы (1.13) находим давление, подставляя значения в единицах СИ: 10 л равны 0,01 м3, масса газа (N·ma) равна произведению молярной массы на количество вещества, т.е. 0,032 кг/моль · 0,25 моль = 0,008 кг:
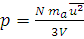 ;
; 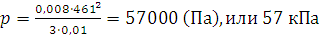
14. При какой температуре средняя квадратичная скорость молекул хлора будет равна 500 м/с?
Решение. Из формулы (1.14) находим T:
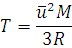
Подставляем значения, выражая их в СИ: ū в м/с, М в кг/моль, а R в Дж/(моль·К), и получаем:
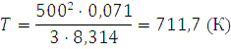
Следовательно, температура t будет равна:
711,7 – 273 = 483,7 (°С)
Дата добавления: 2016-12-26; просмотров: 2636;
