Постановка задачи выбора рациональной организации вагонопотоков на разветвленном участке железной дороги
|
На рисунке стрелками задана некоторая ориентация, принимаемая в качестве "+" (нечетное направление).
В качестве основных исходных данных принимаем величины вагонопотоков, представленные матрицей их корреспонденций:
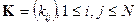 ,
,
где kij - величина вагонопотока назначением из i-ой станции в j-ю;
N - число станций на полигоне.
Для полигона «У» матрица имеет вид:
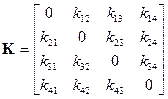 ,
,
В общем случае эта матрица всегда имеет нули на главной диагонали и может быть представлена в виде суммы двух матриц:
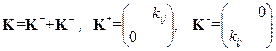 ,
,
в соответствии с ориентацией направления движения (нечетное/четное).
Для подобного разбиения матрицы вагонопотоков на верхнетреугольную ("+" - ориентированную) и нижнетреугольную ("-" - ориентированную) нумерацию станций участка следует задать, пользуясь понятием топологической сортировки .
Для двух смежных станций i, j полагается 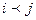 , если на перегоне i-j направление i®j является нечетным ( + ).
, если на перегоне i-j направление i®j является нечетным ( + ).
Известно, что такая топологическая сортировка всегда возможна на ориентированном графе, если он не содержит ориентированных циклов.
Кроме того, следует учитывать разложение матрицы вагонопотоков по признаку состояния подвижного состава (вагоны груженые или порожние):
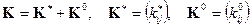
соответственно kij = kij* + kij0 ,
где kij* , kij0 - число груженых и порожних вагонов назначением из i в j, соответственно.
Вагонопоток задается на пространстве назначений, равном
{< станция отправления, станция назначения>} = S ´ S ,
где S - множество станций полигона.
Поездопоток необходимо рассмотреть на пространстве путей. Например, на полигоне "У" поезда назначением из А в D могут следовать одним из четырех путей:
ABD, ACD, ABCD, ACBD.
При этом не рассматриваем случаи, когда поезд циркулирует по замкнутому маршруту, т.е. вкладываем в термин "путь" то же содержание, что и в теории графов: маршрут, не проходящий дважды через одну и ту же вершину графа (станцию). Тем не менее, включаем в модель многогруппные поезда. Так что поезд, следующий по маршруту ABCD, может включать в себя вагоны различных назначений.
Нечетная (+) ориентация задает на множестве S топологическую сортировку, которая является частичной упорядоченностью.
Каждый путь p на полигоне "У" также определяет частичную упорядоченность на S , обозначаемую далее символом 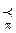 :
:
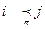
записываем в случае, если станция i предшествует станции j на пути p.
Образуем множество P всех путей на полигоне "У". Каждый вариант организации вагонопотоков соответствует определенному поездопотоку на пространстве путей П.
Для каждого пути pÎP определено множество поездов, следующих по этому пути (назовем это множество поездопотоком пути p):
Vp ={Vp(1),…,Vp(pp)},
где pp - число поездов на маршруте p .
Обозначим å={ Vp }, p Î P множество всех поездопотоков путей. Полный поездопоток, то есть вариант q организации вагонопотоков теперь можно представить как отображение из множества путей во множество поездопотоков путей
q : P®å , q (p)=Vp,
Поскольку каждый поезд следует по участку линейной конфигурации, он в модели может быть задан так же, как общий вагонопоток, то есть матрицей корреспонденций вагонопотока поезда
Vp(k)=(V(k)p,ij)1£i,j£N , 1 £ k £ pp, pÎП,
В этой матрице изменение индексов i, j можно ограничить лишь станциями пути p , причем, если эти индексы расставить не в порядке, принятом при "+" - ориентации всего полигона, а в порядке их следования по маршруту p , то эта матрица всегда будет верхнетреугольной.
Выпишем ограничения на величины вагонопотоков поездов, фиксирующие множество допустимых вариантов организации вагонопотоков:
1) в каждой матрице Vp(k) ненулевыми элементами Vp,ij(k) могут быть только те, у которых i предшествует j на пути p ( ip 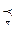 j ), иначе:
j ), иначе:
Vp,ij(k)¹0 (i 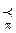 j),
j),
2) по длине или массе поезда:
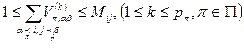 ,
,
 где i, j - смежные станции;
где i, j - смежные станции;
Mij - максимально возможное число вагонов в поезде на участке i - j.
В этом неравенстве фигурирует величина
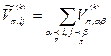 ,
,
равная числу вагонов в поезде Vp(k) на участке i - j;
3) ограничение по максимальной величине вагонопотока:
0 £ Vp,ij(k) £ kij (i 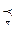 j , 1£ k £pp, pÎP),
j , 1£ k £pp, pÎP),
4) по пропускной способности:
pij + qПij + qлij £ pmaxij ,
где i, j - смежные станции,
pij - число грузовых поездов на участке i-j,
qПij - число пассажирских поездов на участке i-j,
qлij - число поездных локомотивов следующих резервом на участке i-j.
Величина qПij в расчетах принимается фиксированной, а qлij рассчитывается с помощью принципа непарности в зависимости от соотношения четных и нечетных грузовых поездов.
5) По числу сортировочных или сортировочно-отправочных путей на технической станции, используемых при формировании поездов:
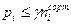
где 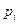 - число грузовых поездов, формируемых на станции i;
- число грузовых поездов, формируемых на станции i;
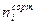 - число сортировочных или сортировочно-отправочных путей на станции i, используемых для формирования поездов;
- число сортировочных или сортировочно-отправочных путей на станции i, используемых для формирования поездов;
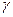 - коэффициент, учитывающий возможность занятия нескольких путей при формировании поезда в одно назначение (
- коэффициент, учитывающий возможность занятия нескольких путей при формировании поезда в одно назначение ( 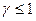 ).
).
6) последнее ограничение является ограничением типа "равенство" и указывает на необходимость полного распределения вагонопотоков по поездам:
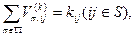
Дата добавления: 2016-12-16; просмотров: 859;
