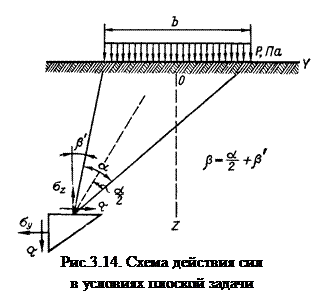
Распределение напряжений в случае плоской задачи. Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями

Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями, длина которых значительно превосходит их поперечные размеры:

,

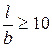где l – длина фундамента; b – ширина фундамента. При этом распределение напряжений под любой частью сооружения, выделенной двумя параллельными сечениями, перпендикулярными оси сооружения, характеризует напряженное состояние под всем сооружением и не зависит от координат, перпендикулярных к направлению загруженной плоскости.

Рассмотрим действие погонной нагрузки в виде непрерывного ряда сосредоточенных сил Р, каждая из которых приходится на единицу длины. В этом случае составляющие напряжений в любой точке М с координатами R и b могут быть найдены по аналогии с пространственной задачей:

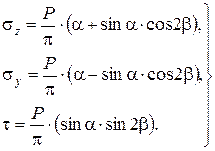(3.27)

Если соотношения геометрических характеристик рассматриваемых точек z, y, b представить в виде коэффициентов влияния K, то формулы для напряжений можно записать так:

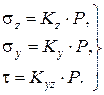(3.28)

Значения коэффициентов влияния K_z, K_y, K_yz табулированы в зависимости от относительных координат z/b, y/b (табл. II.3 приложения II).

Важное свойство плоской задачи в том, что составляющие напряжений t и s_y в рассматриваемой плоскости z0y не зависят от коэффициента поперечного расширения n₀, как в случае пространственной задачи.

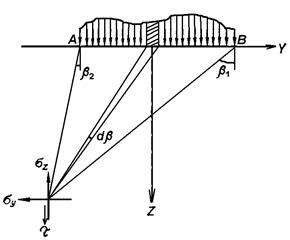
Рис.3.15. Произвольное распределение

нагрузки по ширине полосы b

Если нагрузка распространяется от точки A(b=b₂) до точки B(b=b₁), то, суммируя напряжения от ее отдельных элементов, получим выражения для напряжений в любой точке массива от действия сплошной полосообразной нагрузки.

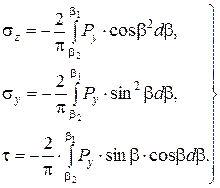(3.29)