Структурно-фазовая деформируемость грунтов

Если передать на поверхность грунта давление через штамп и замерить деформации от каждой ступени нагрузки, то график зависимости между напряжениями и деформациями e (в см) будет иметь вид, показанный на рис.2.29.

Многочисленные исследования показывают, что зависимость между напряжениями и деформациями нелинейна, и в общем виде ее можно записать как

e = a_c s_c+ a _n(s_n -s_c)^m, (2.61)

где a_c и a_n – коэффициенты, определяемые опытом; s_c – напряжение, не превышающее структурной прочности грунта s_c£P_стр; s_n – напряжения, обусловливающие деформации грунта, s_n­-s_c=s; m – параметр нелинейности, определяемый опытным путем.

Коэффициент a_c обратно пропорционален модулю упругости:

.

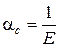Коэффициент a_n зависит от модуля общей деформации E₀:

,

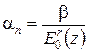где b – коэффициент, зависящий от коэффициента Пуассона; r – параметр, меньший или равный единице, определяется также опытным путем.

При давлениях больше структурной прочности формулу (2.60) можно записать так:

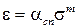, (2.62)

где a_cn – общий коэффициент пропорциональности,

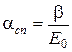. (2.63)

Опыты показали, что при давлениях 0,3…0,5 МПа с достаточной для практики точностью зависимость между напряжениями и деформациями можно принять линейной (отрезок Oa на рис.2.29).

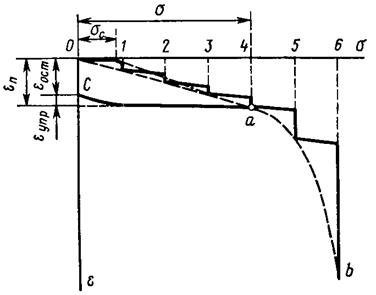
Рис.2.29. Зависимость между напряжениями и деформациями при ступенчатом возрастании нагрузки

В этом случае m = 1 и зависимость между напряжениями и деформациями

e=a_cns. (2.64)

При небольших изменениях давлений зависимость между общими деформациями и напряжениями для грунтов можно принимать линейной - принцип линейной деформируемости.

Деформируемость отдельных компонентов грунта. Напряженно-деформируемое состояние (НДС) скелета грунта, однокомпонентных и квазиоднофазных грунтов можно описать с помощью уравнений (2.61) и (2.64) при t = 0 и t = ¥, т.е. когда процесс перераспределения фаз грунта в единице объема не начался или уже закончился. Для промежуточных отрезков времени НДС грунтов будет зависеть от времени t.

Для практических расчетов часто используют теорию наследственной ползучести Больцмана - Вольтерра. При однократном загружении в течение Dt₀ напряжением s(t₀) относительная деформация скелета грунта e(t) определяется по формуле

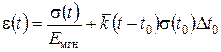. (2.65)

При непрерывном загружении

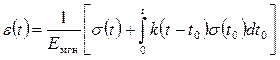, (2.66)

где 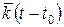– ядро ползучести, .

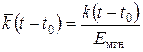Формулы (2.65) и (2.66) показывают, что полная относительная деформация скелета грунта зависит не только от напряженного состояния в начале загружения, но и от предыдущей "истории" нагружения ( ).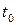

Простейший вид ядра ползучести, дающий хорошую сходимость с опытами, имеет вид

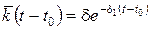, (2.67)

где d и d₁ – параметры ползучести, определяемые опытным путем.

Дегазированная вода имеет модуль упругости порядка 2×10³ МПа. Однако в грунтовой воде всегда имеются пузырьки воздуха и растворенные газы, которые существенно влияют на величину и протекание во времени деформации водонасыщенных грунтов. Коэффициент объемной сжимаемости газосодержащей поровой жидкости можно определить по формуле

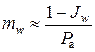, (2.68)

где J_w – коэффициент водонасыщенности грунта; P_a – атмосферное давление, Па.