Собственные векторы и собственные значения линейного оператора. Определение. Пусть R – заданное - мерное линейное пространство
Определение. Пусть R – заданное 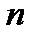 - мерное линейное пространство. Ненулевой вектор
- мерное линейное пространство. Ненулевой вектор 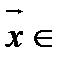 R называется собственным вектором линейного оператора
R называется собственным вектором линейного оператора 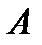 , если найдется такое число
, если найдется такое число 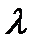 , что выполняется равенство:
, что выполняется равенство:
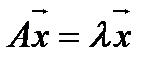 (2)
(2)
Число 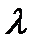 называется собственным числом (значением) линейного оператора
называется собственным числом (значением) линейного оператора 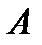 , соответствующим вектору
, соответствующим вектору 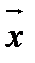 .
.
Если линейный оператор 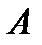 в базисе
в базисе 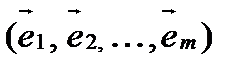 имеет матрицу:
имеет матрицу:
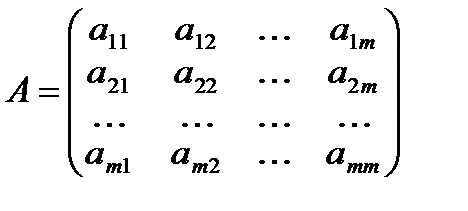 , то собственными числами линейного оператора
, то собственными числами линейного оператора 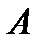 служат действительные корни
служат действительные корни 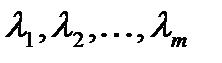 характеристического уравнения
характеристического уравнения 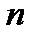 -ой степени, которое можно записать в виде:
-ой степени, которое можно записать в виде:
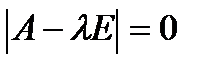 , (3)
, (3)
где 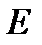 - единичная матрица.
- единичная матрица.
Собственным вектором 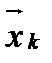 , соответствующим собственному числу
, соответствующим собственному числу 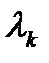 , является любой вектор
, является любой вектор 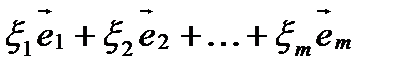 , координаты которого удовлетворяют системе линейных однородных уравнений:
, координаты которого удовлетворяют системе линейных однородных уравнений:
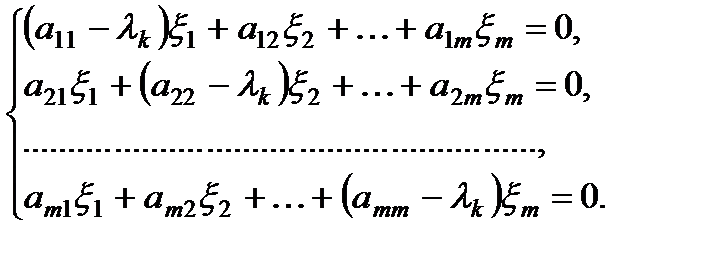 (4)
(4)
Пример 53. Найти собственные числа и собственные векторы линейного оператора  заданного матрицей
заданного матрицей 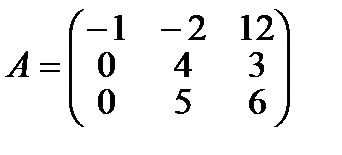 .
.
Решение: составляем характеристическое уравнение используя формулу (3):
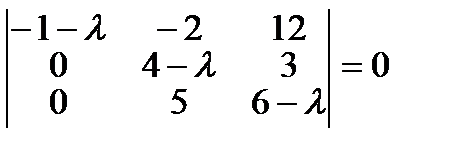 (*)
(*)
Вычислим полученный определитель (понижением порядка):
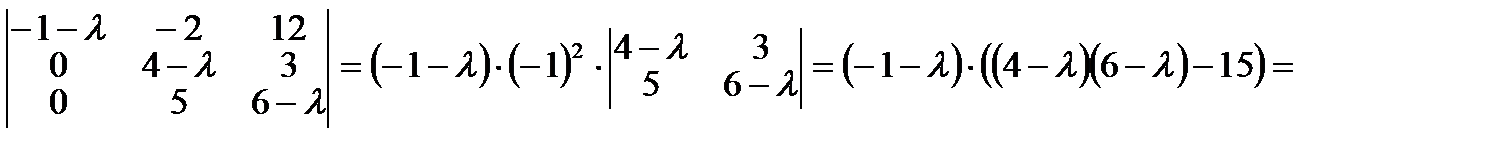
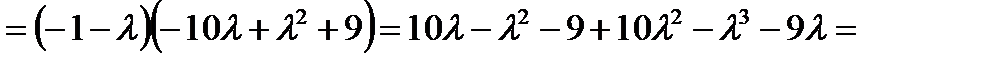
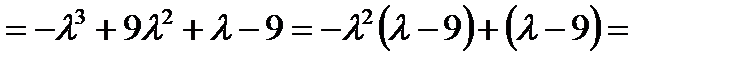
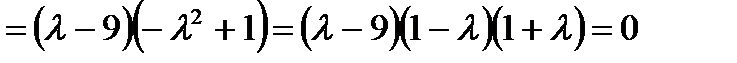
Видно, что  - собственные числа линейного оператора.
- собственные числа линейного оператора.
Найдем собственные векторы.
1) Если 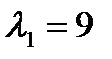 , то для определения координат собственного вектора получаем систему уравнений:
, то для определения координат собственного вектора получаем систему уравнений:
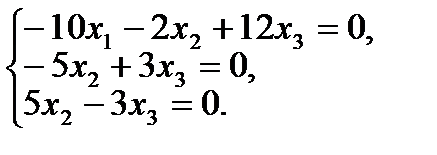
Решим данную систему методом Гаусса:
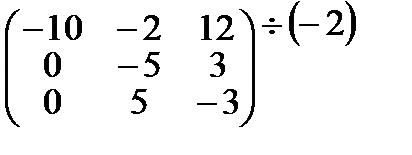 ~
~ 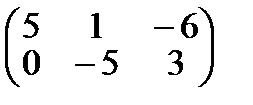
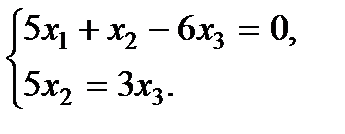
Пусть 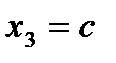 (свободная переменная), тогда
(свободная переменная), тогда 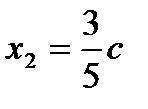 ,
,
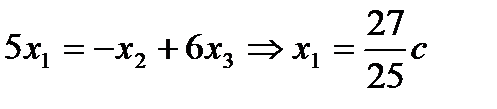 .
.
Получим 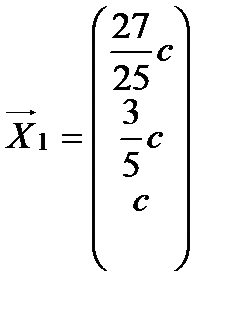 - собственный вектор.
- собственный вектор.
2) Если 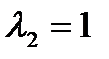 , тогда
, тогда 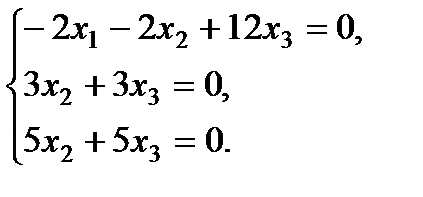 .
.
Решаем систему:
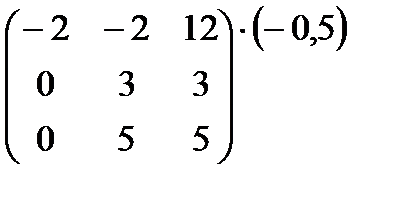 ~
~ 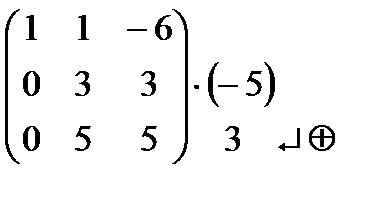 ~
~ 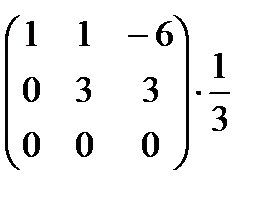 ~
~ 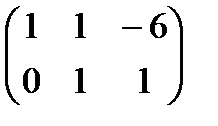 .
.
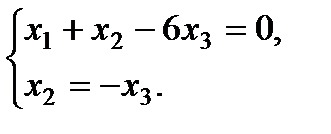 Пусть
Пусть 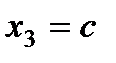 , тогда
, тогда 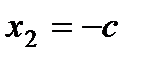 и
и 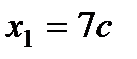 .
.
Получим 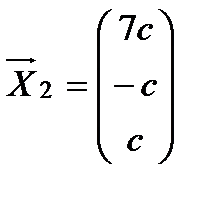 - собственный вектор.
- собственный вектор.
3) Если 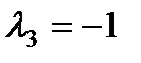 , тогда
, тогда
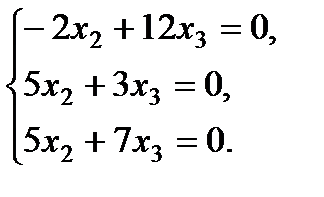 .
.
Решаем систему:
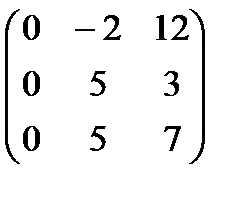 . Пусть
. Пусть 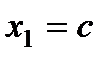 , тогда
, тогда 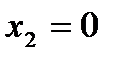 и
и 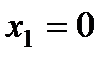 .
.
Получим 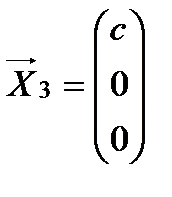 - собственный вектор.
- собственный вектор.
Дата добавления: 2016-05-11; просмотров: 1441;
