Динамические характеристики элементов САУ.

Выше мы получили выражение (2.4), определяющее передаточную функцию линейного элемента системы управления. Это чрезвычайно важное выражение в теории автоматического управления. Оно связывает изображение выходного сигнала Y(s) c изображением входного сигнала Х(s) через динамические свойства элемента системы управления.

Ясно, что входное воздействие может иметь произвольный вид. Однако, чтобы охарактеризовать наиболее существенные черты динамического поведения объекта управления можно использовать некоторые "стандартные" виды входных воздействий. При этом выходной сигнал будет содержать определенную информацию о свойствах объекта управления.

Такие "стандартные" виды воздействий называются типовыми входными воздействиями. К ним относятся:

1) Единичная ступенчатая функция: 1(t).

2) Единичная импульсная функция: δ(t).

3) Гармонические функции: sin(ωt) и cos(ωt).

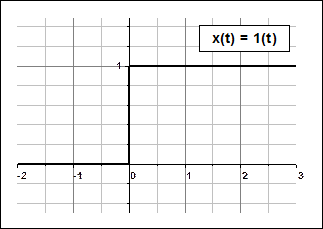
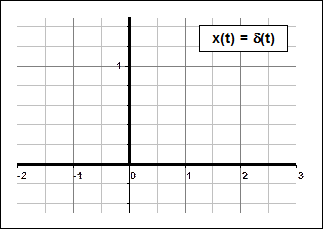
а) б)

Рис. 2.4. Единичная ступенчатая функция а) и единичная импульсная функция б).

Математически эти функции описываются следующим образом:

; .

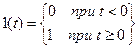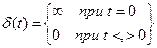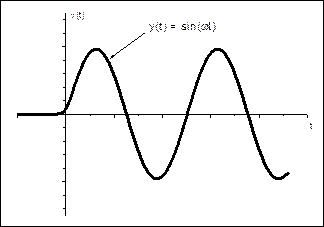
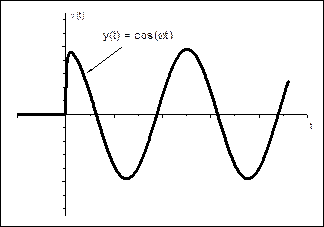
Рис. 2.5. Гармонические функции.

Динамической характеристикой любого элемента системы управления называется его реакция на типовое входное воздействие. В зависимости от вида типового воздействия разделяют временные и частотные характеристики.

Временные характеристики:

§ переходная характеристика h(t);

§ весовая функция или импульсная переходная функция w(t).

7.Динамические характеристики элементов САУ. Частотные характеристики.

Частотные характеристики:

§ амплитудно-фазовая частотная характеристика (АФЧХ) или частотная передаточная функция;

§ амплитудная частотная характеристика (АЧХ);

§ фазовая частотная характеристика (ФЧХ);

§ логарифмическая амплитудная частотная характеристика (ЛАЧХ либо ЛАХ);

§ логарифмическая фазовая частотная характеристика (ЛФЧХ либо ЛФХ).

Перечисленные выше характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Эти характеристики являются исчерпывающим описанием динамических свойств звена.