Устойчивость рыночного равновесия

Проблема устойчивости рыночного равновесия всегда волновала экономистов-теоретиков, так как выводы о стабильности системы имеют далеко идущие последствия о степени государственного вмешательства (или невмешательства) в ход экономического развития.

При анализе устойчивости равновесия следует использовать динамические модели, в которых учитывается фактор времени. В качестве примера возьмем «паутинообразную» простейшую модель.

Данная модель поведения производителей предполагает ряд допущений, которые упрощают действительность. Во-первых, производители не могут корректировать ранее принятые решения о каких-то объемах производства (например, картофеля или пшеницы). Во-вторых, не допускается возможность образования запасов с последующей их реализацией, и не учитываются случайные явления (например, колебания урожайности). Причем производитель основывает свои ожидания будущей цены на фактической цене, которая имела место на рынке, в частности, в период посевной компании, то есть на цене предшествующего периода:

Q_St = S (P_t-1),

где Q_St - объем предложения товара в период времени t, P_t-1 - фактическая цена товара в период времени t-1.

В отличие от производителей потребители не принимают решения об объемах закупок заранее. Поэтому объем спроса в любой период зависит от цены товара в данном периоде:

Q_dt = D (P_t)

где Q_dt - объем спроса на товар в период t; P_t - цена товара в период t.

Представим эту ситуацию графически (рис. 18). Вышеназванные зависимости объемов спроса и объемов предложения

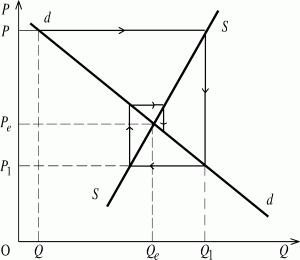
от цены отражают соответственно линии dd и SS. Если предположить, что в какой-то начальный период времени (t = 0) по цене P было раскуплено товара в количестве Q, то в следующий период (t = 1) этого товара будет предложено к продаже в количестве Q₁. Однако данный объем предложения может быть реализован лишь по цене P₁. В дальнейшем рыночная ситуация будет развиваться таким образом, что сокращение предложения и увеличение спроса станет происходить соответственно движению паутинообразной линии, которая стремится к положению равновесия в точке с координатами P_e и Q_e, где равновесие является наиболее устойчивым.

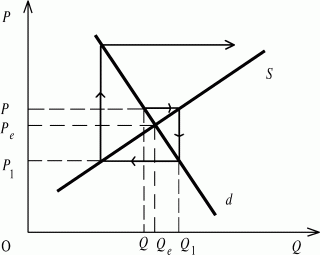
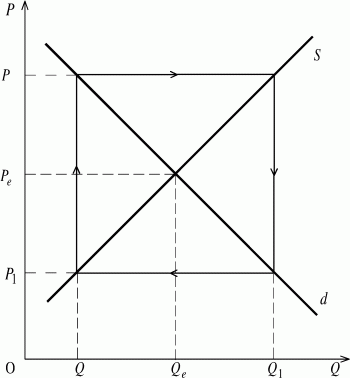
Следовательно, в паутинообразной модели заложены колебания цен и объемов продукции, которые при одних условиях приводят к равновесию, а при других - удаляют от него. Равновесие является устойчивым, если линия предложения имеет больший угол наклона в соотвествующую сторону, чем линия спроса (рис. 18). Hа графике неустойчивого равновесия наблюдается обратная картина (рис. 19). Когда же углы наклона линий спроса и предложения одинаковы, то совершаются равномерные циклические колебания названных параметров (рис. 20).

Как показано на рисунках, в состоянии устойчивого равновесия цена совершает затухающие колебания (рис. 21). В случаях отклонения для цены характерны как нарастающие колебания с постепенным удалением от точки равновесия (рис. 22), так и равномерные колебательные движения вокруг этой точки (рис. 23).

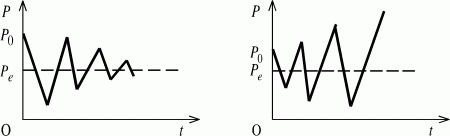
Hадо сказать, что на практике два последних варианта колебаний не очень реалистичны, так как рыночная система обладает стабилизирующими факторами. Дело в том, что рано или поздно производители скорректируют процедуру определения будущей цены, например, на основе анализа динамики цен за несколько предшествующих периодов. Создание запасов товаров и их конъюнктурное изменение может также повлиять на стабилизацию рыночного равновесия.