Уточнення коренів. Метод проб
Попередній підрозділ був присвячений першому з етапів наближеного розв’язання алгебраїчних і трансцендентних рівнянь – відділенню коренів.
Другий етап – уточнення коренів, тобто доведення їх до заданого ступеня точності.
Дано рівняння 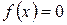 , де
, де 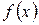 – неперервна функція. Треба знайти корінь цього рівняння
– неперервна функція. Треба знайти корінь цього рівняння 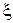 з точністю до ε, де ε – деяке додатне достатньо мале число.
з точністю до ε, де ε – деяке додатне достатньо мале число.
 |
Вважатимемо, що корінь 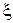 відділений і знаходиться на відрізку [а, b], тобто має місце нерівність
відділений і знаходиться на відрізку [а, b], тобто має місце нерівність 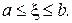 Числа а і b є наближеними значеннями кореня відповідно з недостачею і з надлишком. Похибка цих наближень не перевищує довжини відрізка b – а. Якщо
Числа а і b є наближеними значеннями кореня відповідно з недостачею і з надлишком. Похибка цих наближень не перевищує довжини відрізка b – а. Якщо 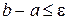 , то бажана точність обчислень досягнута, і за наближене значення кореня
, то бажана точність обчислень досягнута, і за наближене значення кореня 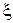 можна прийняти або а, або b. Але якщо
можна прийняти або а, або b. Але якщо 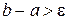 , то бажана точність обчислень не досягнута і необхідно звузити інтервал, в якому знаходиться корінь
, то бажана точність обчислень не досягнута і необхідно звузити інтервал, в якому знаходиться корінь 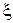 , тобто підібрати такі числа
, тобто підібрати такі числа 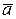 і
і 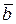 , щоб виконувалася нерівність
, щоб виконувалася нерівність 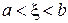 і
і 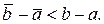 При
При 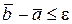 обчислення треба зупинити і за наближене значення кореня з точністю до ε прийняти або
обчислення треба зупинити і за наближене значення кореня з точністю до ε прийняти або 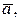 або
або 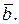 Треба відмітити, що значення кореня буде більш точним, коли за наближене значення кореня прийняті не кінці відрізка
Треба відмітити, що значення кореня буде більш точним, коли за наближене значення кореня прийняті не кінці відрізка 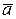 і
і 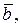 а середина цього відрізка, тобто
а середина цього відрізка, тобто 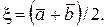 Помилка при цьому не буде перевищувати величину
Помилка при цьому не буде перевищувати величину 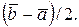
Метод проб. Нехай дано рівняння 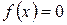 , де
, де 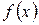 – неперервна функція, і корінь
– неперервна функція, і корінь 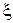 відділений на відрізку [а, b], тобто
відділений на відрізку [а, b], тобто 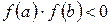 , при чому
, при чому 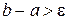 . Треба знайти корінь цього рівняння
. Треба знайти корінь цього рівняння 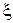 з точністю до ε (рис. 8).
з точністю до ε (рис. 8).
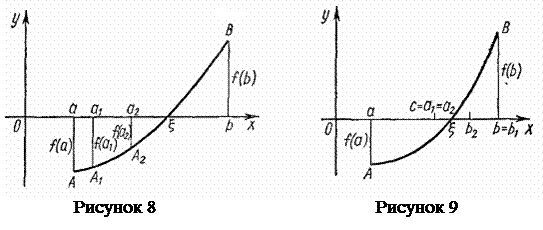 |
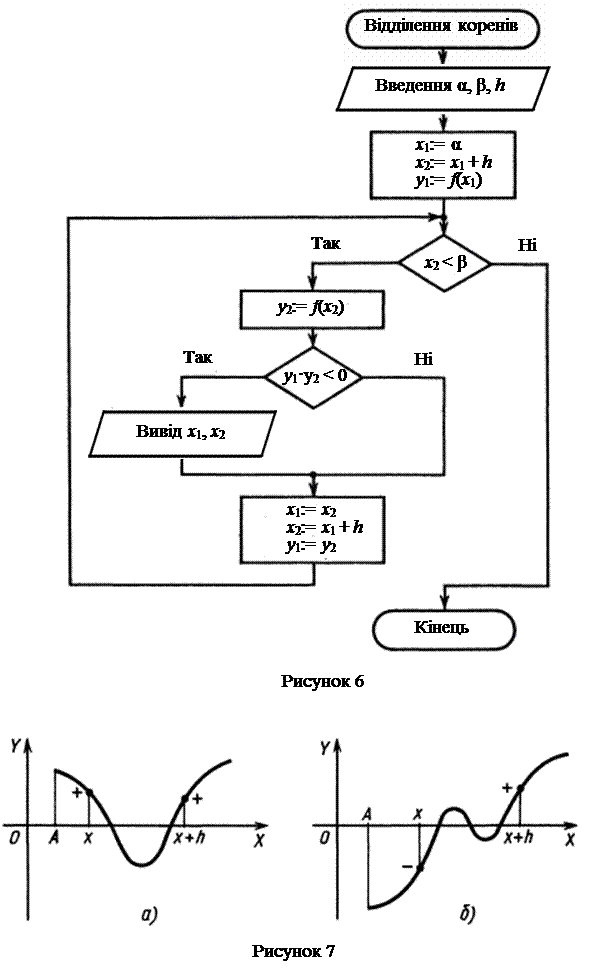
На відрізку [а, b] вибирають довільним чином точку а1, яка розділить його на два відрізки [а, а1] і [а1, b]. З цих двох відрізків вибирають той, на кінцях якого функція приймає значення з протилежними знаками. У нашому прикладі
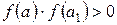 і
і 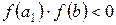 , тому вибирають відрізок [а1, b]. Потім на цьому звуженому відрізку знову довільним чином беруть точку а2 і знаходять знаки добутків
, тому вибирають відрізок [а1, b]. Потім на цьому звуженому відрізку знову довільним чином беруть точку а2 і знаходять знаки добутків 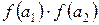 і
і 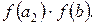 Оскільки
Оскільки 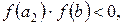 то вибирають відрізок [а2, b]. Цей процес продовжують до тих пір, поки довжина відрізка, на якому знаходиться корінь, не стане меншою ε. Корінь ξ отримують як середньоарифметичне значення кінців найденого відрізка, причому помилка кореню не перевищуватиме
то вибирають відрізок [а2, b]. Цей процес продовжують до тих пір, поки довжина відрізка, на якому знаходиться корінь, не стане меншою ε. Корінь ξ отримують як середньоарифметичне значення кінців найденого відрізка, причому помилка кореню не перевищуватиме 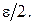
Метод половинного ділення. Метод проб у такому вигляді, як описаний вище на ЕОМ не застосовується. Для складання програми і проведення розрахунків на ЕОМ метод проб застосовується у вигляді так званого метода половинного ділення, який в літературі з числових методів можна знайти під назвою "метод дихотомії".
Нехай корінь ξ рівняння 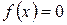 , де
, де 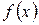 – неперервна функція, і корінь
– неперервна функція, і корінь 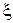 відділений на відрізку [а, b], тобто
відділений на відрізку [а, b], тобто 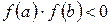 , при чому
, при чому 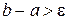 . Треба знайти корінь цього рівняння
. Треба знайти корінь цього рівняння 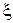 з точністю до ε.
з точністю до ε.
Як і раніше, візьмемо на відрізку [а, b] проміжну точку а1, однак не довільним чином, а так щоб вона знаходилася в середині відрізка, тобто 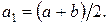 Ця точка розділить [а, b] на два відрізки [а, а1] і [а1, b], довжина яких дорівнює
Ця точка розділить [а, b] на два відрізки [а, а1] і [а1, b], довжина яких дорівнює 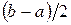 (рис. 9). Якщо
(рис. 9). Якщо 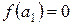 , то а1 буде коренем рівняння
, то а1 буде коренем рівняння 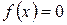 . Якщо ж
. Якщо ж 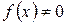 , то з двох відрізків [а, а1] і [а1, b], що утворилися, вибирають той, на кінцях якого функція
, то з двох відрізків [а, а1] і [а1, b], що утворилися, вибирають той, на кінцях якого функція 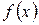 приймає значення протилежних знаків. Ітераційний процес продовжують за схемою, розглянутою вище, до тих пір поки не буде знайдено корінь рівняння з заданою точністю, або інакше – поки відрізок [а, b] не стане меншим за ε.
приймає значення протилежних знаків. Ітераційний процес продовжують за схемою, розглянутою вище, до тих пір поки не буде знайдено корінь рівняння з заданою точністю, або інакше – поки відрізок [а, b] не стане меншим за ε.
Треба відмітити, що функція 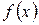 розраховується з деякою похибкою ε1. З цих двох відрізків вибираємо той, на кінцях якого функція приймає значення з протилежними знаками. У нашому прикладі
розраховується з деякою похибкою ε1. З цих двох відрізків вибираємо той, на кінцях якого функція приймає значення з протилежними знаками. У нашому прикладі 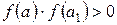 і
і 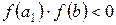 , тому вибираємо відрізок [а1, b].
, тому вибираємо відрізок [а1, b].
Процес ділення відрізка навпіл продовжують до тих пір, коли на якомусь n-му етапі або середина буде коренем рівняння (випадок, який рідко зустрічаються на практиці), або буде отриманий відрізок 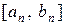 такий, що
такий, що 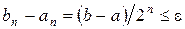 і
і 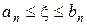 (число n вказує на кількість проведених ділень). Числа an і bn – корні рівняння
(число n вказує на кількість проведених ділень). Числа an і bn – корні рівняння 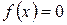 з точністю до ε. За наближене значення кореня треба взяти
з точністю до ε. За наближене значення кореня треба взяти 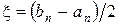 , причому похибка не буде перевищувати
, причому похибка не буде перевищувати 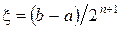
Зазначимо, що при практичній програмній реалізації методу половинного ділення (методу дихотомії) замість розрахунку добутку 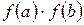 , пов’язаного з визначенням однаковості або різниці знаків функції
, пов’язаного з визначенням однаковості або різниці знаків функції 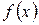 в точках a і b, доцільно скористатися стандартною підпрограмою-функцією SIGN(X) , яка в тому чи іншому вигляді присутня в усіх алгоритмічних мовах. Значення, що видається цією підпрограмою-функцією, відповідає наступному математичному визначенню:
в точках a і b, доцільно скористатися стандартною підпрограмою-функцією SIGN(X) , яка в тому чи іншому вигляді присутня в усіх алгоритмічних мовах. Значення, що видається цією підпрограмою-функцією, відповідає наступному математичному визначенню:
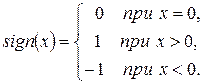
Подібна заміна в алгоритмі методу половинного ділення обґрунтовується тим, що при наближенні точок a і b до кореню рівняння при розрахунку добутку 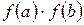 може статися зникнення порядку внаслідок малості співмножників. Тому використання знакової функції є переважним.
може статися зникнення порядку внаслідок малості співмножників. Тому використання знакової функції є переважним.
Оскільки при зменшенні інтервалу 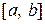 в процесі половинного ділення точка а завжди залишається зліва від шуканого кореня, то, не дивлячись на її переміщення, знак
в процесі половинного ділення точка а завжди залишається зліва від шуканого кореня, то, не дивлячись на її переміщення, знак 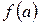 не буде змінюватися. Тому знак
не буде змінюватися. Тому знак 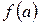 визначається тільки один раз, а в процесі ділення вихідного інтервалу узнають знак тільки в середній точці
визначається тільки один раз, а в процесі ділення вихідного інтервалу узнають знак тільки в середній точці 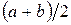 і порівнюють його на збіг або розходження зі знаком
і порівнюють його на збіг або розходження зі знаком 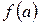 . При збігу точку а переміщують в середину відрізка, в протилежному випадку переміщують точку b.
. При збігу точку а переміщують в середину відрізка, в протилежному випадку переміщують точку b.
Метод хорд
 |
Метод хорд є одним із поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. Він, як і метод половинного ділення, призначений для уточнення кореня рівняння на інтервалі
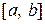 , на кінцях якого ліва частина рівняння
, на кінцях якого ліва частина рівняння 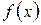 приймає різні знаки. На відміну від методу половинного ділення чергове наближення в методі хорд береться не в середині відрізку, а в точці х1, в якій пряма лінія, проведена через точки
приймає різні знаки. На відміну від методу половинного ділення чергове наближення в методі хорд береться не в середині відрізку, а в точці х1, в якій пряма лінія, проведена через точки 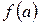 і
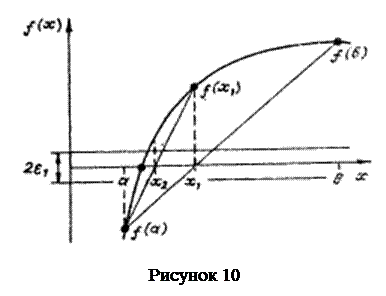
і 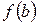 , перетинає вісь абсцис (рис. 10). Отже, ідея методу хорд полягає в тому, що на достатньо малому проміжку
, перетинає вісь абсцис (рис. 10). Отже, ідея методу хорд полягає в тому, що на достатньо малому проміжку 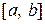 дуга кривої
дуга кривої 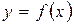 замінюється стягуючою її хордою і за наближене значення кореня приймається точка перетину хорди з віссю абсцис.
замінюється стягуючою її хордою і за наближене значення кореня приймається точка перетину хорди з віссю абсцис.
За новий інтервал для продовження ітераційного процесу вибирають той з двох 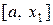 або
або 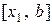 , на кінцях якого функція
, на кінцях якого функція 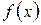 приймає значення з різними знаками.
приймає значення з різними знаками.
Процес уточнення кореня закінчується, коли відстань між черговими наближеннями буде менше заданої похибки ε1
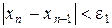
або коли значення функції 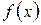 попадуть в область шуму, тобто
попадуть в область шуму, тобто
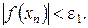
Рівняння прямої лінії, що проходить через точки 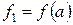 і
і 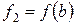 має вигляд
має вигляд
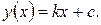
Коефіцієнти k і c рівняння цієї прямої визначають наступним чином
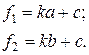
Розв’язавши цю систему рівнянь, отримують
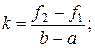
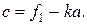
Точку перетину прямої 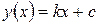 з віссю абсцис знаходять, прирівнюючи
з віссю абсцис знаходять, прирівнюючи 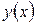 до нуля
до нуля
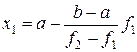
або
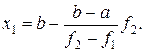
На завершення треба відзначити, що в більшості випадків при розв’язанні рівнянь методом хорд застосовується менша кількість ітерацій порівняно з методом половинного ділення.
Дата добавления: 2016-11-02; просмотров: 1045;
