Оценка значимости параметров взаимосвязи
Получив оценки корреляции и регрессии, необходимо проверить их на соответствие истинным параметрам взаимосвязи.
Существующие программы для ЭВМ включают, как правило, несколько наиболее распространенных критериев. Для оценки значимости коэффициента парной корреляции рассчитывают стандартную ошибку коэффициента корреляции:
| s | = | 1- rxy | (8.8) | |||||
| rxy | ||||||||
| n - 2 | ||||||||
| В первом приближении нужно, чтобы s r | < rxy . Значимость rxy проверяется его | |||||||
| xy |

сопоставлением с s rxy , при этом получают:




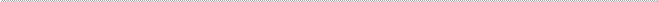

| tрасч. = rxy × | n - 2 | (8.9) | |||
| - rxy | |||||

где tрасч – так называемое расчетное значение t-критерия.

Если tрасч больше теоретического (табличного) значения критерия Стьюдента (tтабл.) для заданного уровня вероятности и (n-2) степеней свободы, то можно утверждать, что rxy значимо.
Подобным же образом на основе соответствующих формул рассчитывают стандартные ошибки параметров уравнения регрессии, а затем и t-критерии для каждого параметра. Важно опять-таки проверить, чтобы соблюдалось условие tрасч > tтабл. В противном случае доверять полученной оценке параметра нет оснований.
Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, вычисляя его расчетное значение:




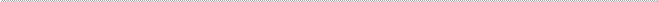

| Fрасч. = | R2 | (n - m) | (8.10) | |
| (1- R2 )(m -1) | ||||
где n – число наблюдений;
m –число параметров уравнения регрессии.

Fрасч также должно быть больше Fтеор при v1 = (m-1)и v2 = (n-m)степенях свободы.В противном случае следует пересмотреть форму уравнения, перечень переменных и т.д.
Дата добавления: 2016-10-17; просмотров: 609;
