Индивидуальные индексы и их применение в экономическом анализе

Индекс –это относительная величина,показывающая,во сколько раз уровеньизучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различие условий может проявляться во времени (тогда говорят об индексах динамики), в пространстве (территориальные индексы), в выборе в качестве базы сравнения какого-либо условного уровня, например планового показателя, уровня договорных обязательств и т.п. Соответственно вводят индекс выполнения обязательств или, если плановый уровень сравнивается с уровнем предыдущего периода, – индекс планового задания.
В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но главным образом для определения экономической значимости причин, объясняющих абсолютное различие сравниваемых уровней.
Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня этого явления в других условиях.
Так, уровень товарооборота в виде суммы выручки от продажи товара в условиях отчетного года Q1 сравнивается с аналогичной суммой выручки базисного года Q0. В итоге получаем индивидуальный индекс товарооборота:
| iQ = Q1 / Q0 , | (7.1) |
Аналогичные индивидуальные индексы можно рассчитать и для любого интересующего нас показателя. В частности, поскольку сумма выручки определяется ценой товара (р) и количеством продаж в натуральном измерении (q), можно определить индивидуальные индексы цены ip и количества проданных товаров – iq:




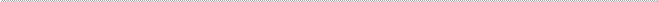
 iq = p1 / p0 , iq = q1 - q0 (7.2)
iq = p1 / p0 , iq = q1 - q0 (7.2)

С аналитической точки зрения iq показывает, во сколько раз увеличилась (или уменьшилась) общая сумма выручки под влиянием изменения объема продажи в натуральных единицах.
Аналогично ip показывает, во сколько раз изменилась общая сумма выручки под влиянием изменения цены товара. Очевидно, что
| i | = i | q | × i | или Q | = Q | i | q | × i | p | (7.3) | |
| Q | p |
Вторая формула представляет двухфакторную индексную мультипликативную модель итогового показателя, в данном случае – объема товарооборота. Посредством такой модели находят прирост итога под влиянием каждого фактора в отдельности.
Так, если выручка от продажи некоторого товара возросла с 8 млн. руб. в предыдущем периоде до 12,180 млн. руб. в последующем и известно, что это объясняется увеличением количества проданного товара на 5 % при цене на 45 % большей, чем в предыдущем периоде, то можно записать следующее соотношение:
12,180 = 8 × 1,05 × 1,45 (млн. руб.).
Очевидно, что общий прирост выручки в сумме 12,180-8 = 4,180 млн. руб. объясняется изменением объема продажи и цены. Прирост выручки за счет изменения объема продажи (в натуральном выражении) составит:
| DQ(q) = Q0 × (iq - 1) | (7.4) |
| или в нашем примере: | |
| DQ(q)=8×(1,05-1)=0,40млн.руб. | |
| Тогда за счет изменения цены данного товара сумма выручки изменилась на: | |
| DQ(q)=(Q1- Q0)- DQ(q)= Q1- Q0×iq = Q0×iq ×(ip -1) | (7.5) |
или
DQ(p) = 8 ×1,05 ×(1,45 -1) = 3,78млн.руб.
Очевидно, что общий прирост товарооборота складывается из приростов, объясняемых каждым фактором в отдельности, т.е.
| DQ = Q1 - Q0 = DQ(q) + DQ(p) | (7.6) |
или
DQ = 12,18 - 8 = 0,40 + 3,78 = 4,18млн.руб
Можно заметить, что существует и другой способ распределения общего прироста по факторам в двухфакторной индексной мультипликативной модели, а именно:
| DQ(q) = Q0 ×iq ×(iq -1) и DQ(p) = Q0 ×(ip -1), | (7.7) |
В нашем примере общий прирост выручки (4,18 млн. руб.) объясняется теперь:
- изменением цены:
DQ(p) = 8 ×(1,45 -1) = 3,60млн.руб
- изменением объема продажи:
DQ(q) = 8 ×1,45 ×(1,05 -1) = 0,58млн.руб
Выбор конкретной формы разложения общего прироста итога должен определяться конкретными условиями развития изучаемого показателя, в данном случае – конъюнктурой спроса-предложения. В экономической практике и большинстве научных рекомендаций в настоящее время преобладает первое направление, когда сначала выясняют вклад в общий прирост количественного фактора при базисном уровне качественного признака (цен), а затем – вклад качественного фактора (цены) в расчете на отчетный уровень количественного показателя (объема – q).
Дата добавления: 2016-10-17; просмотров: 549;
