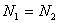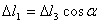Расчет статически неопределимых систем по способу допускаемых нагрузок.
Совсем другие результаты мы получим, если будем применять способ допускаемых нагрузок к статически неопределимым системам, стержни которых изготовлены из материала, обладающего способностью к большим пластическим деформациям, например из малоуглеродистой стали.
В качестве примера рассмотрим систему из трех стержней, нагруженных силой Q (рис. 2). Пусть все стержни сделаны из малоуглеродистой стали с пределом текучести 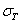 . Длины крайних стержней, как и выше, обозначим
. Длины крайних стержней, как и выше, обозначим 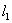 ; длину среднего
; длину среднего 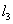 . Допускаемое напряжение
. Допускаемое напряжение 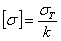
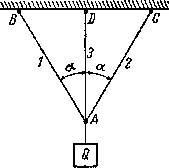
Рис.2. Расчетная схема однократно статически неопределимой стержневой системы.
Как и раньше, при расчете этой статически неопределимой системы зададимся отношением площадей стержней; примем, что все три стержня будут иметь одинаковую площадь F. Получим:
Используя закон Гука, получим:
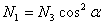
Следовательно:
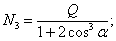
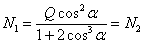
Так как 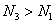 , средний стержень напряжен больше, чем крайние; поэтому подбор площади сечения F надо произвести по формуле:
, средний стержень напряжен больше, чем крайние; поэтому подбор площади сечения F надо произвести по формуле:
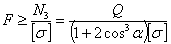
Ту же величину площади надо дать и боковым стержням; в них получается некоторый дополнительный запас.
Применим способ допускаемых нагрузок; условием прочности будет:
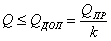
Что в данном случае следует понимать под предельной нагрузкой конструкции? Так как конструкция выполнена из материала, имеющего площадку текучести, то, по аналогии с простым растяжением стержня из такого материала, за предельную нагрузку следует взять груз, соответствующий достижению состояния текучести для всей конструкции в целом. Назовем эту нагрузку 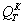 . Пока сила Q не достигла этого значения, для дальнейшей деформации (опускания точки A) требуется возрастание нагрузки. Когда же Q сделается равным
. Пока сила Q не достигла этого значения, для дальнейшей деформации (опускания точки A) требуется возрастание нагрузки. Когда же Q сделается равным 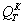 , дальнейший рост деформаций будет происходить уже без увеличения нагрузки, — конструкция выйдет из строя.
, дальнейший рост деформаций будет происходить уже без увеличения нагрузки, — конструкция выйдет из строя.
Для определения величины 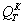 рассмотрим постепенный ход деформации нашей стержневой системы. Так как средний стержень напряжен сильнее крайних, то в нем раньше, чем в других, напряжение дойдет до предела текучести. Нагрузку, соответствующую этому моменту, обозначим QТ; она будет равна:
рассмотрим постепенный ход деформации нашей стержневой системы. Так как средний стержень напряжен сильнее крайних, то в нем раньше, чем в других, напряжение дойдет до предела текучести. Нагрузку, соответствующую этому моменту, обозначим QТ; она будет равна:
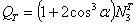
где 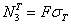 — усилие в среднем стержне, соответствующее его пределу текучести.
— усилие в среднем стержне, соответствующее его пределу текучести.
Напряжения в крайних стержнях, имеющих ту же площадь, в этот момент еще не дойдут до предела текучести, и эти стержни будут упруго сопротивляться дальнейшей деформации. Для того чтобы эта деформация происходила, необходимо дальнейшее увеличение нагрузки до тех пор, пока в крайних стержнях напряжения тоже не дойдут до предела текучести. Лишь тогда будет достигнута предельная грузоподъемность конструкции 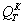 .
.
Так как при нагрузке QТ напряжения в среднем стержне дойдут уже до предела текучести 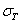 , то при дальнейшем возрастании груза они, а стало быть и усилие N3, останутся без увеличения. Наша статически неопределимая система превратится в статически определимую, состоящую из двух стержней АВ и АС и нагруженную в точке А силой Q, направленной вниз, и известным усилием
, то при дальнейшем возрастании груза они, а стало быть и усилие N3, останутся без увеличения. Наша статически неопределимая система превратится в статически определимую, состоящую из двух стержней АВ и АС и нагруженную в точке А силой Q, направленной вниз, и известным усилием 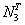 , равным
, равным 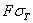 (Рис.3).
(Рис.3).
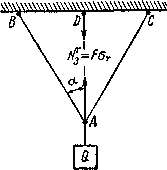
Рис.3. Эквивалентная статически определимая система
Такая схема работы нашей конструкции будет иметь место, пока
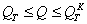
Для иллюстрации хода деформации рассматриваемой конструкции изобразим графически зависимость между силой Q и перемещением f точки А (Рис. 4). Пока 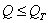 опускание точки А равно удлинению среднего стержня и определяется формулой
опускание точки А равно удлинению среднего стержня и определяется формулой
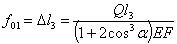

Рис.4. Динамика деформации в зависимости от нагрузочной способности системы
Как только Q будет заключаться в промежутке 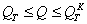 перемещение точки А должно быть вычислено, как опускание этого узла в системе двух стержней АС и АВ, нагруженных в точке А силой
перемещение точки А должно быть вычислено, как опускание этого узла в системе двух стержней АС и АВ, нагруженных в точке А силой 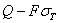
 . Так как:
. Так как:
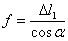
и, в свою очередь:

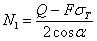
Отсюда
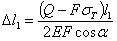
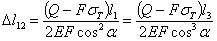
Для f12 (на втором участке) получаем уравнение прямой, но уже не проходящей через начало координат. После достижения нагрузкой Q значения 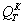 напряжения в крайних стержнях достигнут предела текучести, и система будет деформироваться без увеличения нагрузки. График перемещения идет теперь параллельно оси абсцисс.
напряжения в крайних стержнях достигнут предела текучести, и система будет деформироваться без увеличения нагрузки. График перемещения идет теперь параллельно оси абсцисс.
Для определения предельной грузоподъемности всей системы 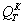 мы должны для системы двух стержней, нагруженных силой
мы должны для системы двух стержней, нагруженных силой 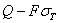 , найти то значение Q, при котором напряжения и в крайних стержнях дойдут до предела текучести. Такая задача решена в предыдущем параграфе; подставляя в выражение (а) § 26 вместо Р величину
, найти то значение Q, при котором напряжения и в крайних стержнях дойдут до предела текучести. Такая задача решена в предыдущем параграфе; подставляя в выражение (а) § 26 вместо Р величину 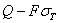 , получаем:
, получаем:
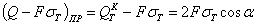
Отсюда
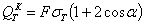
Допускаемая нагрузка будет равна
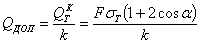
а учитывая, что
 ,
,
получаем
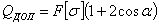
Окончательно:
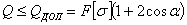
и
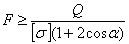
Эта величина меньше, чем полученная обычным методом расчета, т. е.
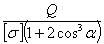
При 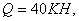
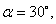
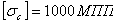 (сталь) получаем: по обычному способу
(сталь) получаем: по обычному способу
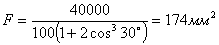
по способу допускаемых нагрузок:
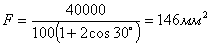
Таким образом, метод расчета по допускаемым нагрузкам позволяет спроектировать статически неопределимую систему из материала, обладающего площадкой текучести, экономичнее, чем при расчете по допускаемым, напряжениям. Это понятно: при способе расчета по допускаемым напряжениям мы считали за предельную нагрузку нашей конструкции величину QТ, при которой до предела текучести доходил лишь материал среднего стержня, крайние же были недонапряжены. При методе расчета по допускаемым нагрузкам предельная грузоподъемность определяется величиной 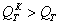 . При нагрузке
. При нагрузке 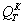 полностью используется материал всех трех стержней.
полностью используется материал всех трех стержней.
Таким образом, новый метод расчета позволяет реализовать скрытые при старом способе запасы прочности в статически неопределимых системах, добиться повышения их расчетной грузоподъемности и действительной равнопрочности всех частей конструкции. Не представит никаких затруднений распространить этот метод на случай, когда соотношение площадей среднего и крайних стержней не будет равно единице.
Изложенные выше теоретические соображения проверялись неоднократно на опыте, причем всегда наблюдалась достаточно близкая сходимость величин предельной нагрузки — вычисленной и определенной при эксперименте. Это дает уверенность в правильности теоретических предпосылок метода допускаемых нагрузок.
Лекция № 14. Учет собственного веса при растяжении и сжатии.
Дата добавления: 2016-10-17; просмотров: 573;