Круги Мора (пряма задача)

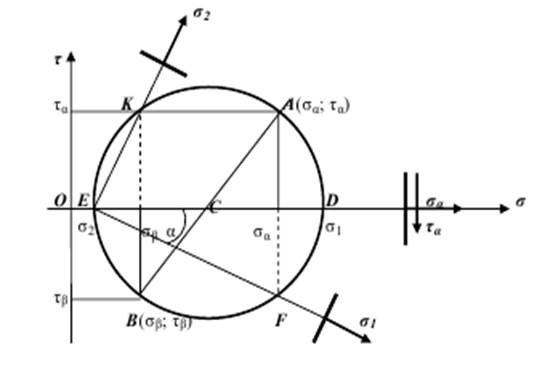
Круг Мора – це геометричне місце точок (у випадку плоского напруженого стану – коло), координати яких відповідають чисельним значенням нормальних і дотичних напружень, що діють у точці на площадках, які мають різні кути нахилу. Тобто круг Мора – це геометрична інтерпретація напруженого стану в певній точці навантаженого твердого тіла.

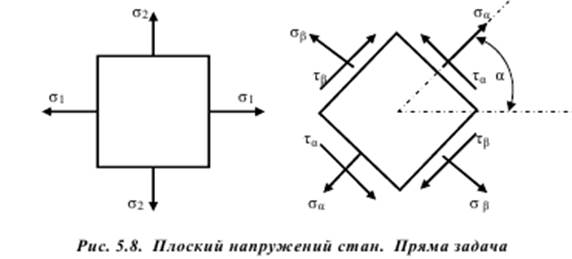
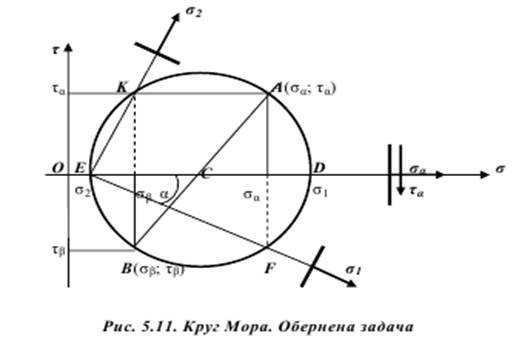
Тепер отримаємо аналітичні залежності для розв’язування оберненої задачі. Для цього можна або розглянути залежності (5.7; 5.10) або вивести їх за допомогою круга Мора.

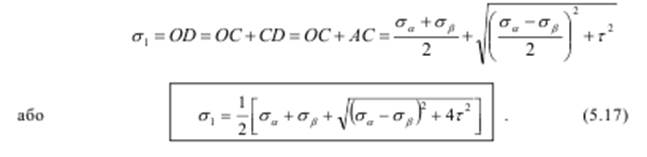
Лекція №8

Деформований стан в точці. Узагальнений закон Гука.

План лекції:

8.1. Узагальнений закон Гука.

8.2. Об’ємна деформація.

8.1. Узагальнений закон Гука.

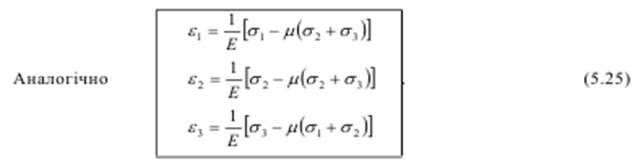
Залежності (5.25) називають узагальненим законом Гука для ізотропного тіла. Ці вирази справедливі не тільки для головних, але й для будь-яких трьох взаємно перпендикулярних напрямків, оскільки при малих деформаціях вплив зсуву на лінійну деформацію є малою величиною другого порядку.

8.2. Об’ємна деформація.

Лекція №9

Критерії пластичності і руйнування. Теорії міцності

План лекції:

9.1. Питома потенціальна енергія зміни форми.

9.2. Теорії міцності.

9.2.1. І теорія міцності.

9.2.2. ІІ теорія міцності.

9.2.3. ІІІ теорія міцності.

9.2.4. Критерій Мора

9.1. Питома потенціальна енергія зміни форми.

Питома потенціальна енергія деформації u − це енергія, яка накопичується в елементарному об’ємі тіла при його пружній деформації. Повну питому потенціальну енергію при розгляді деяких процесів доцільно уявити у вигляді суми двох компонент u_v − питомої потенціальної енергії, яка йде на зміну об’єму; та u_ф − питомої потенціальної енергії, яка йде на зміну форми.

Уявивши собі деформацію, коли змінюється об’єм, але форма залишається незмінною, використовуючи закон Гука та вводячи поняття усереднених напружень і деформацій, неважко вивести формулу

9.3. Теорії міцності

Міцність тіла, що знаходиться у складному напруженому стані, навряд чи може бути оцінена порівнянням із допустимим напруженням тільки одного, нехай і найбільшого напруження.

9.2.5. І теорія міцності

Перше найпростіше припущення полягає в тому, що небезпечний стан матеріалу настає в той момент, коли найбільше за абсолютною величиною нормальне напруження досягає небезпечного значення. Цю гіпотезу називають теорією найбільших напружень або першою теорією міцності.

Таким чином, і в загальному випадку, коли всі три головні напруження σ1,σ2 і σ3 не дорівнюють нулю, при перевірці за цією теорією необхідно враховувати величину лише найбільшого розтягуючого та найбільшого стискаючого напруження. Величини ж двох інших головних напружень відсутні і, начебто, ніякого впливу на міцність матеріалу, на досягнення ним небезпечного стану не впливають і про них при перевірці міцності можна забути. Тоді до певної міри втрачається відмінність між перевіркою міцності при лінійному напруженому стані та при об'ємному.

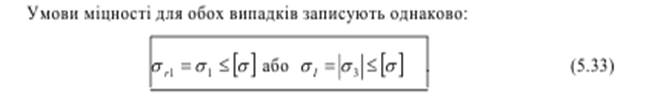
При перевірці вказаної гіпотези дослідами виявилася невідповідність її висновків із результатами дослідів на всебічний стиск не тільки пластичних матеріалів, але й крихких.

Лише для випадку розтягу крихких матеріалів ця теорія узгоджується з дослідами. Оскільки ця теорія дає або зайві, або недостатні розміри перетинів елементів конструкцій при складному напруженому стані, її не застосовують і вона має лише історичне значення.

9.2.6. ІІ теорія міцності

Висунута недоліками першої, і певною мірою на противагу їй, друга гіпотеза пропонує виникнення небезпечного стану визначати не рівнем найбільшого напруження, а величиною найбільшого відносного видовження (або вкорочення).

Якщо це так, то перевірку міцності слід проводити за найбільшими відносними деформаціями. Зберігаючи той же коефіцієнт запасу, для найбільшої відносної поздовжньої деформації в загальному випадку (всі головні напруження не дорівнюють нулю) за допустиму ми повинні вибирати ту ж величину, що і при простому розтягу.

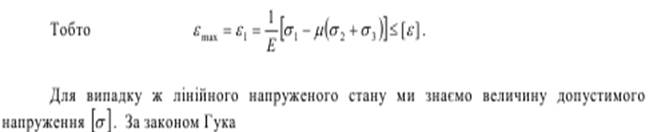
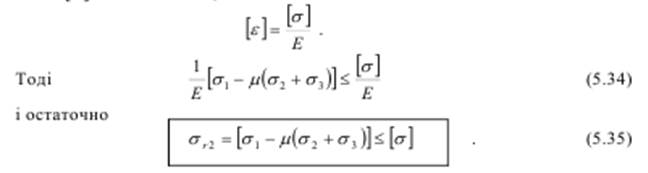
Ця гіпотеза також суперечить результатам досліджень міцності пластичних матеріалів. Якби вона була для таких матеріалів вірна, то зразок, що розтягується в двох або трьох напрямах, був би міцнішим за зразок, який розтягується лінійно. Досвід цього не підтверджує. Не підтверджується ця гіпотеза і при всесторонньому рівномірному стиску. Для крихкого стану матеріалу теорія найбільших відносних деформацій дає результати, що, як правило, узгоджуються з дослідом.

9.2.7. ІІІ теорія міцності

Третя гіпотеза міцності (або теорія найбільших дотичних напружень) стверджує, що головну роль у виникненні небезпечного стану матеріалу відіграє найбільше напруження, але вже не нормальне, а дотичне, що дорівнює напіврізниці найбільшого і найменшого головних напружень:

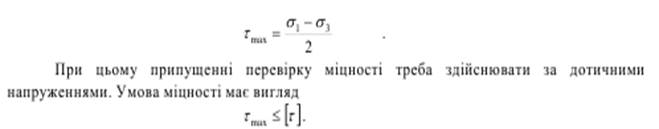
Третя умова міцності достатньо близько узгоджується з результатами дослідів, особливо для пластичних матеріалів. Вона підтверджується дослідами на всебічний стиск.

Ця теорія забезпечує міцність елементів конструкцій, що розраховуються.

У тому простому вигляді розрахункових напружень (5.36) умова міцності може бути написана лише для тих матеріалів, для яких допустимі напруження на розтяг і стиск можуть бути прийняті рівними, наприклад, для сталі. Для таких матеріалів, як чавун, камінь і т. д. в умову (5.36) необхідно внести зміни, які вперше запропонував Х.Мор.

9.2.4. Критерій Мора

Формули (5.39) і (5.40) представляють умову міцності за теорією найбільшої потенціальної енергії зміни форми.