Модель пространства состояний системы
Приведем еще одну формальную модель (она подробно рассмотрена в работе [54]). Эта модель очень проста, однако она позволяет сформулировать, что нам нужно делать, чтобы не попасть в тупиковое состояние.
 ' Напомним, что деревом в теории графов называют граф, не имеющий циклов.
' Напомним, что деревом в теории графов называют граф, не имеющий циклов.
260_______________________ Глава 8. Проблема тупиков и методы борьбы с ними
Пусть состояние операционной системы сводится к состоянию различных ресурсов в системе (свободны они или выделены какому-нибудь процессу). Состояние системы изменяется процессами, когда они запрашивают, приобретают или освобождают ресурсы — это единственно возможные действия (точнее, мы принимаем во внимание только такие действия). Если процесс не блокирован в данном состоянии, он может изменить это состояние на новое. Однако так как в общем случае невозможно знать априори, какой путь может избрать произвольный процесс в своей программе (это неразрешимая проблема!), то новое состояние может быть любым из конечного числа возможных. Следовательно, процессы нами будут трактоваться как недетерминированные объекты. Введенные ограничения на известные понятия приводят нас к нескольким формальным определениям.
□ Система есть пара 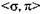 , где
, где
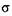 — множество состояний системы
— множество состояний системы 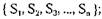
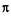 — множество процессов
— множество процессов 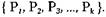
□ Процесс Р; есть частичная функция, отображающая состояние системы в непу
стые подмножества ее же состояний. Это обозначается так:
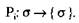
Если процесс Р; определен на состоянии S, то область значений 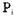 обозначается как
обозначается как 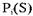 . Если
. Если 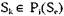 , то мы говорим, что
, то мы говорим, что 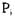 может изменить состояние S,. в
может изменить состояние S,. в
состояние Sk посредством операции, и используем обозначение 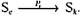 Наконец, запись
Наконец, запись  означает, что
означает, что 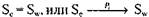 для некоторо-
для некоторо-
го i, или 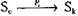 для некоторых i и Sk, причем
для некоторых i и Sk, причем 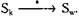
Другими словами, система может быть переведена посредством n > О операций с помощью m > 0 различных процессов из состояния St. в состояние Sw. Мы говорим, что процесс заблокирован в данном состоянии, если он не может изменить состояние, то есть в этом состоянии процесс не может ни требовать, ни получать, ни освобождать ресурсы. Поэтому справедливо следующее. Процесс Р: заблокирован в состоянии S,,, если не существует ни одного состояния
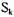 ,такого что
,такого что 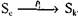 , причем
, причем 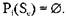
Далее, мы говорим, что процесс 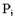 находится в тупике в данном состоянии
находится в тупике в данном состоянии 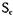 , если он заблокирован в состоянии
, если он заблокирован в состоянии 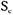 и если вне зависимости от того, какие операции (изменения состояний) произойдут в будущем, процесс
и если вне зависимости от того, какие операции (изменения состояний) произойдут в будущем, процесс 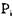 остается заблокированным. Поэтому дадим еще одно определение.
остается заблокированным. Поэтому дадим еще одно определение.
Процесс 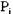 находится в тупике в состоянии
находится в тупике в состоянии 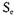 , если для всех состояний
, если для всех состояний 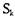 , таких что
, таких что 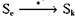 , процесс Р, блокирован в состоянии
, процесс Р, блокирован в состоянии 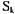
Приведем пример. Определим систему 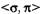 :
:
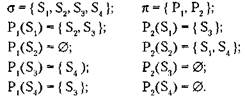
формальные модели для изучения проблемы тупиковых ситуаций_______________ 261
Некоторые возможные последовательности изменений для этой системы таковы:
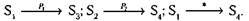
Последовательность  может быть реализована, например, следующим
может быть реализована, например, следующим
образом: 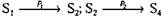 или же
или же 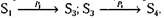
Заметим, что процесс 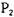 находится в тупике как в состоянии
находится в тупике как в состоянии 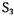 , так и в состоянии
, так и в состоянии 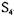 ; для последнего случая
; для последнего случая  или
или 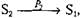 и процесс
и процесс 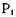 не оказыва-
не оказыва-
ется заблокированным ни в 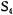 , ни в
, ни в 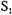
Диаграмма переходов этой системы изображена на рис. 8.7.
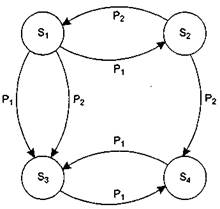
Рис. 8.7. Пример системы <!!!!!!!!!!!!!!!!!!!!о, я> на четыре состояния
Состояние S называется тупиковым, если существует процесс 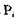 , находящийся в тупике в состоянии S.
, находящийся в тупике в состоянии S.
Теперь мы можем сказать, что, по определению, тупик предотвращается при введении такого ограничения на систему, чтобы каждое ее возможное состояние не было тупиковым состоянием. Введем еще одно определение.
Состояние 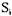 есть безопасное состояние, если для всех
есть безопасное состояние, если для всех 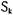 , таких что
, таких что 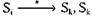 не является тупиковым состоянием.
не является тупиковым состоянием.
Рассмотрим еще один пример системы 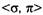 . Граф ее состояний приведен на
. Граф ее состояний приведен на
рис. 8.8. Здесь состояния S2 и S3 являются безопасными; из них система никогда не сможет попасть в тупиковое состояние. Состояния S, и S4 могут привести как к безопасным состояниям, так и к опасному состоянию S5. Состояния S6 и S7 являются тупиковыми.
Наконец, в качестве еще одной простейшей системы вида <!!!!!!!!!!!а, п> приведем пример тупика с ресурсами типа SR, уже рассмотренный нами ранее и проиллюстрированный рис. 8.3. Для этого определим состояния процессов Pj и Р2, которые используют ресурсы R, и R2 (табл. 8.1).
Пусть состояние системы 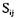 означает, что процесс
означает, что процесс 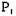 находится в состоянии
находится в состоянии 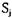 , а процесс Р2 — в состоянии
, а процесс Р2 — в состоянии 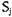 . Возможные изменения в пространстве состояний
. Возможные изменения в пространстве состояний
262_______________________ Глава 8, Проблема тупиков и методы борьбы с ними
этой системы изображены на рис. 8.9. Вертикальными стрелками показаны возможные переходы из одного состояния в другое для процесса Р,, а горизонтальными — для процесса Р2. В данной системе имеется три опасных состояния: S22, S23 и S32. Попав в любое из них, мы неминуемо перейдем в тупиковое состояние S33.
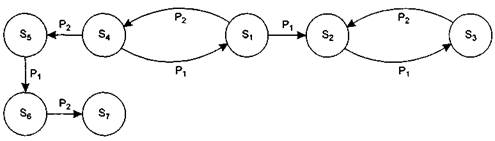
Рис. 8.8. Пример системы <а, !!!!!!!!!!п> с безопасными, опасными и тупиковым состояниями
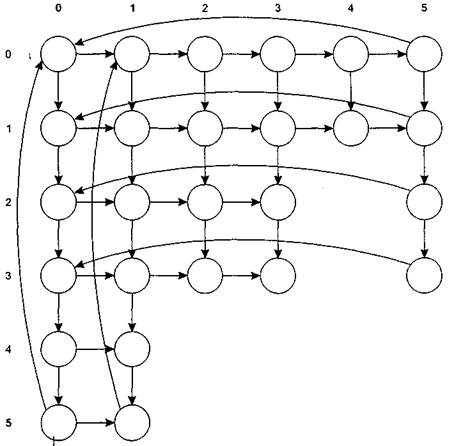
Рис. 8.9. Модель системы из двух процессов
Методы борьбы с тупиками____________________________________________ 263
Таблица 8.1. Состояния процессов Р, и Р2 при использовании ресурсов R, и R2
 Р, Описание Р2 Описание
Р, Описание Р2 Описание
0  Не держит никаких ресурсов 0 Не держит никаких ресурсов
Не держит никаких ресурсов 0 Не держит никаких ресурсов
1 Запросил ресурс R2l не держит 1 Запросил ресурс R,, не держит
никаких ресурсов никаких ресурсов
2 Держит ресурс R2 2 Держит ресурс R,
3 Запросил ресурс R,, держит ресурс R2 3 Запросил ресурс R2, держит ресурс R,
4 Держит ресурсы R, и R2 4 Держит ресурсы R, и R2
5 Держит ресурс R2 после освобождения 5 Держит ресурс R2 после освобождения
ресурса R, ресурса R,
 Теперь, когда мы знаем понятия надежного, опасного и безопасного состояний, можно рассмотреть методы борьбы с тупиками.
Теперь, когда мы знаем понятия надежного, опасного и безопасного состояний, можно рассмотреть методы борьбы с тупиками.
Дата добавления: 2016-09-20; просмотров: 773;
