Потребность потребностей

А 2 3 6 1

В 3 2 7 2

С______________ 2__________ 3_________ 5________________ _0________________________

Последний столбец в таблице показывает нам, сколько еще единиц ресурса может затребовать каждый из процессов, если бы он получил ресурс на свой текущий запрос.

Если запрос процесса А будет удовлетворен первым, то он в принципе может за­просить еще одну единицу ресурса R, и уже в этом случае мы получим тупиковую ситуацию, поскольку ни один из наших процессов не сможет продолжить свои вычисления. Следовательно, при выполнении запроса процесса А мы попадаем в ненадежное' состояние.

Если первым будет выполнен запрос процесса В, то у нас останется свободной еще одна единица ресурса R. Однако если процесс В запросит еще две, а не одну едини­цу ресурса R, а он может это сделать, то мы опять получим тупиковую ситуацию.

Если же мы сначала выполним запрос процесса С и выделим ему не две (как про­цессу В), а все три единицы ресурса R, то у нас не останется никакого резерва, но процесс С сможет благополучно завершиться и вернуть системе все свои ресурсы, поскольку на этом его потребности в ресурсах заканчиваются. Это приведет к тому, что свободное количество ресурса R станет равно пяти. После этого уже можно будет удовлетворить запрос либо процесса В, либо процесса А, но не обоих сразу.

Часто бывает так, что последовательность запросов, связанных с каждым процес­сом, заранее не известна. Но если заранее известен общий запрос на ресурсы каж­дого типа, то выделение ресурсов можно контролировать. В этом случае необходи­мо для каждого требования, в предположении, что оно удовлетворено, определить, существует ли среди общих запросов от всех процессов некоторая последователь-

¹ Термин «ненадежное состояние» не предполагает, что в данный момент существует или в какое-то время обязательно возникнет тупиковая ситуация. Он просто говорит о том, что в случае некоторой неблагоприятной последовательности событий система может зайти в тупик.

266_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

ность требований, которая может привести к опасному состоянию. Данный под­ход является примером контролируемого выделения ресурса.

Классическое решение этой задачи предложено Дейкстрой и известно как алго­ритм банкира [53]. Алгоритм банкира напоминает процедуру принятия решения о том, может ли банк безопасно для себя дать взаймы денег. Принятие решения основывается на информации о потребностях клиента (нынешних и максимально возможных в принципе) и учете текущего баланса банка. Хотя этот алгоритм прак­тически нигде не используется, рассмотрим его, так как он интересен с методичес­кой и академической точек зрения.

Пусть существует N процессов, для каждого из которых известно максимальное количество потребностей в некотором ресурсе R (обозначим эти потребности че­рез Max(i)). Ресурсы выделяются не сразу все, а в соответствии с текущим запро­сом. Считается, что все ресурсы i-ro процесса будут освобождены по его завершении. Количество полученных ресурсов для i-ro процесса обозначим Получ(i). Остаток в потребностях i-ro процесса на ресурс R обозначим через Остаток(i). Признак того, что процесс может не завершиться, — это значение false для переменной Заверш(i). Наконец, переменная Своб_рес будет означать количество свободных единиц ре­сурса R, а максимальное количество ресурсов в системе определено значением Все-го_рес. Текст программы алгоритма банкира приведен в листинге 8.4.

Листинг 8.4.Алгоритм банкира Дейкстры

Begin

Своб_рес := Всего_рес: For i := 1 to N do Begin

Своб_рес := Своб_рес - Получ(i); Остаток(i) := Max(i) - Получ(i): Заверш(i) := false: { процесс может не завершиться } End:

flag := true: { признак продолжения анализа } while flag do begin

flag := false: for i := 1 to N do begin

if ( not ( Заверш(i)) )) and ( Остаток(i) <= Своб_рес ) then begin

Заверш(i)) := true: Своб_рес := Своб_рес + Получ(i)); Flag := true End End End; If Своб_рес - Bcero_pec

then Состояние системы безопасное.

и можно выдать ресурс else Состояние небезопасное.

и выдавать ресурс нельзя end.

Каждый раз, когда что-то может быть выделено из числа остающихся незанятыми ресурсов, предполагается, что соответствующий процесс работает, пока не окон-

Методы борьбы с тупиками____________________________________________ 267

чится, а затем его ресурсы освобождаются. Если в конце концов все ресурсы осво­бождаются, значит, все процессы могут завершиться и система находится в безопас­ном состоянии. Другими словами, согласно алгоритму банкира система удовлет­воряет только те запросы, при которых ее состояние остается надежным. Новое состояние безопасно тогда и только тогда, когда каждый процесс может окончить­ся. Именно это условие и проверяется в алгоритме банкира. Запросы процессов, приводящие к переходу системы в ненадежное состояние, не выполняются и от­кладываются до момента, когда их можно будет выполнить.

Алгоритм банкира позволяет продолжать выполнение таких процессов, которым в случае системы с предотвращением тупиков пришлось бы ждать. Хотя алгоритм банкира относительно прост, его реализация может обойтись довольно дорого. Основным накладным расходом стратегии обхода тупика с помощью контролиру­емого выделения ресурса является время выполнения алгоритма, так как он вы­полняется при каждом запросе. Причем, алгоритм работает наиболее медленно, когда система близка к тупику. Необходимо отметить, что обход тупика неприме­ним при отсутствии информации о требованиях процессов на ресурсы.

Рассмотренный алгоритм примитивен, в нем учитывается только один вид ресур­са, тогда как в реальных системах количество различных типов ресурсов бывает очень большим. Были опубликованы варианты этого алгоритма для большого числа различных типов системных ресурсов. Однако все равно алгоритм не получил рас­пространения. Причин тому несколько.

□ Алгоритм исходит из того, что количество распределяемых ресурсов в системе
фиксировано. Иногда это не так, например вследствие неисправности отдель­
ных устройств.

□ Алгоритм требует, чтобы пользователи заранее указывали свои максимальные
потребности в ресурсах. Это чрезвычайно трудно реализовать. Часть таких све­
дений, конечно, могла бы предоставлять система программирования, но все
равно оставшуюся часть информации о потребностях в ресурсах должны
давать пользователи. Однако чем более дружественными по отношению к
пользователям становятся компьютеры, тем чаще встречаются пользователи,
которые не имеют ни малейшего представления о том, какие ресурсы им потре­
буются.

D Алгоритм требует, чтобы число работающих процессов оставалось постоянным. Очевидно, что это требование также, в общем, нереалистично, особенно в муль-титерминальных системах и в условиях, когда пользователь запускает несколько параллельных процессов.

Обнаружение тупика

Чтобы распознать тупиковое состояние, необходимо для каждого процесса опре­делить, сможет ли он когда-либо снова развиваться, то есть изменять свои состоя­ния. Так как нас интересует возможность развития процесса, а не сам процесс сме­ны состояния, то достаточно рассмотреть только самые благоприятные изменения состояния.

268_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

Очевидно, что незаблокированный процесс (имеющий все необходимые ресурсы или только что получивший ресурс и поэтому пока незаблокированный) через не­которое время освобождает все свои ресурсы и затем благополучно завершается. Освобождение ранее занятых ресурсов может «разбудить» некоторые ранее за­блокированные процессы, которые, в свою очередь, развиваясь, смогут освободить другие ранее занятые ресурсы. Это может продолжаться до тех пор, пока либо не останется незаблокированных процессов, либо какое-то количество процессов все же останется заблокированными. В последнем случае (если существуют заблоки­рованные процессы при завершении указанной последовательности действий) начальное состояние S является состоянием тупика, а оставшиеся процессы нахо­дятся в тупике в состоянии S. В противном случае S не есть состояние тупика.

Обнаружение тупика посредством редукции графа повторно используемых ресурсов

Наиболее благоприятные условия для незаблокированного процесса Р_; могут быть представлены редукцией (сокращением) графа повторно используемых ресурсов (см. описание модели Холта ранее в разделе «Понятие тупиковой ситуации при выполнении параллельных вычислительных процессов»). Редукция графа может быть описана следующим образом.

- Граф повторно используемых ресурсов сокращается процессом Р_:, который не является ни заблокированной, ни изолированной вершиной, путем удаления всех ребер, входящих в вершину Р_: и выходящих из P_h Эта процедура является эквивалентной приобретению процессом Р, неких ресурсов, на которые он ра­нее выдавал запросы, а затем освобождению всех его ресурсов. Тогда Pj стано­вится изолированной вершиной.

- Граф повторно используемых ресурсов несокращаем (не редуцируется), если

он не может быть сокращен ни одним процессом. - Граф ресурсов типа SR является полностью сокращаемым, если существует

последовательность сокращений, которая удаляет все дуги графа.

Лемма: для ресурсов типа SR порядок сокращений дуг графа повторно используе­мых ресурсов несуществен; все последовательности ведут к одному и тому же не­сокращаемому графу.

Допустим, что лемма неверна. Тогда должно существовать некоторое состояние S, которое сокращается до некоторого несокращаемого состояния S, с помощью пос­ледовательности seq, и до несокращаемого состояния S₂ с помощью последователь­ности seq₂ так, что 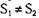(то есть все процессы в состояниях S, и S₂ или заблокиро­ваны, или изолированы).

Если сделать такое предположение, то мы приходим к противоречию, которое устраняется только при условии, что S, = S₂. Действительно, предположим, что последовательность seq, состоит из упорядоченного списка процессов (Р„ Р₂, .... Р_к). Тогда последовательность seq, должна содержать процесс Р, который не содер­жится в последовательности seq₂. В противном случае S, = S₂, потому что редукция графа только удаляет дуги, уже существующие в состоянии S, а если последо­вательности seq, и seq₂ содержат одно и то же множество процессов (пусть и в раз-

Методы борьбы с тупиками____________________________________________ 269

личном порядке), то должно быть удалено одно и то же множество дуг. И доказа­тельство по индукции покажет, что 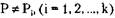приводит к нашему проти­воречию.

- Имеет место соотношение 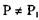, так как вершина S может быть редуцирована
процессом Р, а состояние S₂ должно, следовательно, также содержать процесс Р,.

- Пусть 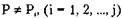. Однако поскольку после редукции процессами P_i?

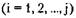возможно еще сокращение графа процессом P_j+I, это же самое дол­жно быть справедливо и для последовательности seq₂ независимо от порядка следования процессов. То же самое множество ребер графа удаляется с помо­щью процесса Р;. Таким образом,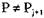

Следовательно, 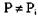для i = 1, 2,..., к и Р не может существовать, а это противоре-

чит нашему предположению, что 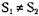. Следовательно, Si = S₂.

Теорема о тупике: Состояние S есть состояние тупика тогда и только тогда, когда граф повторно используемых ресурсов в состоянии S не является полностью со­кращаемым.

- Для доказательства предположим, что состояние S есть состояние тупика, и
процесс Pi находится в тупике в S. Тогда для всех 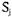, таких что про­
цесс Pj заблокирован в состоянии Sj (по определению). Так как сокращения гра­
фа идентичны для серии операций процессов, то конечное несокращаемое
состояние в последовательности сокращений должно оставить процесс Pj бло­
кированным. Следовательно, граф не является полностью сокращаемым.

- Предположим теперь, что состояние S не является полностью сокращаемым. Тогда существует процесс Р,, который остается заблокированным при всех воз­можных последовательностях операций редукции в соответствии с леммой (см. выше). Так как любая последовательность операций редукции графа по­вторно используемых ресурсов, оканчивающаяся несокращаемым состоянием, гарантирует, что все ресурсы типа SR, которые могут когда-либо стать доступ­ными, в действительности освобождены, то процесс Р_; навсегда заблокирован и, следовательно, находится в тупике.

Первое следствие: процесс Р; не находится в тупике тогда и только тогда, когда серия сокращений приводит к состоянию, в котором Р_: не заблокирован.

Второе следствие: если S есть состояние тупика (по ресурсам типа SR), то по край­ней мере два процесса находятся в тупике в S.

Из теоремы о тупике непосредственно следует и алгоритм обнаружения тупиков. Нужно просто попытаться сократить граф по возможности эффективным спосо­бом; если граф полностью не сокращается, то начальное состояние было состояни­ем тупика для тех процессов, вершины которых остались в несокращенном графе. Рассмотренная нами лемма позволяет предложить алгоритмы обнаружения тупи­ка. Например, можно представить систему посредством графа повторно использу­емых ресурсов и попробовать выполнить его редукцию, причем делать это следу­ет, стараясь упорядочивать сокращения удобным образом.

Граф повторно используемых ресурсов может быть представлен матрицами или списками. В обоих случаях экономия памяти может быть достигнута за счет взве-

270_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

шенных ориентированных мультиграфов (слиянием определенных дуг получения или дуг запроса между конкретным ресурсом и данным процессом в одну дугу с соответствующим весом, определяющим количество единиц ресурса).

Рассмотрим вариант с матричным представлением. Поскольку граф двудольный, он представляется двумя матрицами размером n x m. Одна матрица — матрица распределения 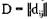, в которой элемент 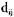отражает количество единиц R, ре-

сурса, выделенного процессу 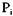, то есть 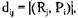где 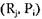— это дуга между

вершинам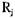и и 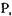.ведущая из 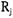в Pj. Вторая матрица — матрица запросов ,

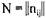где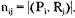

В случае использования связанных списков для отображения той же структуры можно построить две группы списков. Ресурсы, выделенные некоторому процессу 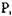, связаны с 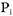указателями:

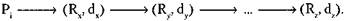
Здесь 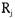— вершина, представляющая ресурс, 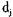— вес дуги, то есть 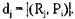Подобным образом и ресурсы, запрошенные процессом 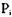, связаны вместе.

Аналогичные списки создаются и для ресурсов (списки распределенных и запро­шенных ресурсов):

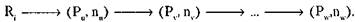
Здесь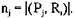

Для обоих представлений удобно также иметь одномерный массив доступных еди­ниц ресурсов 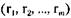, где г, обозначает число доступных (нераспределенных единиц) ресурса 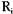, то есть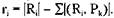

Простой метод прямого обнаружения тупика заключается в просмотре по порядку списка (или матрицы) запросов, причем, где возможно, производятся сокращения дуг графа до тех пор, пока нельзя будет сделать более ни одного сокращения. При этом самая плохая ситуация возникает, когда процессы упорядочены в некоторой последовательности 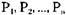, а единственно возможным порядком сокращений

является обратная последовательность, то есть 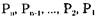, а также в случае,

когда процесс запрашивает все m ресурсов. Тогда число проверок процессов равно:

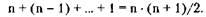
Таким образом, время выполнения такого алгоритма в наихудшем случае пропор­ционально 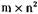, поскольку каждая проверка требует испытания m ресурсов.

Более эффективный алгоритм может быть получен за счет хранения некоторой дополнительной информации о запросах. Для каждой вершины процесса 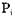опре­деляется так называемый счетчик ожиданий w, отображающий количество ресур­сов (не число единиц ресурса), которые в какое-то время вызывают блокировку процесса. Кроме того, можно сохранять для каждого ресурса запросы, упорядо­ченные по размеру (числу единиц ресурса). Тогда следующий алгоритм сокраще­ний, записанный на псевдокоде, имеет максимальное время выполнения, пропор­циональное m х n.

Методы борьбы с тупиками____________________________________________ 271

For all P !!!!!!!!!!1 L do

Begin for all R₃ з |(Rj.P)| > 0 do Begin r, := i-j + |(R,.P)|:

For all P, э 0 < "| CPi.Rj) | <= Tj do Begin w, := w, - 1;

If w, = 0 then L := L U {Pi}
End
End
End
Deadlock := Not (L = {PI. P2... Pn}):

Здесь L — это текущий список процессов, которые могут выполнять редукцию гра­фа. Можно сказать, что L = {P_f | w, = 0}. Программа выбирает процесс Р из списка L, процесс Р сокращает граф, увеличивая число доступных единиц rj всех ресурсов fy, распределенных процессу Р, обновляет счетчик ожидания w, каждого процесса Р₍, который сможет удовлетворить свой запрос на частный ресурс Rj, и добавляет Р₍ к L, если счетчик ожидания становится нулевым.

Методы обнаружения тупика по наличию замкнутой цепочки запросов

Структура графа обеспечивает простое необходимое (но не достаточное) условие для тупика. Для любого графа G = <Х, Е> и вершины х I X пусть Р(х) обозначает множество вершин, достижимых из вершины х, то есть

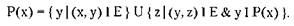
Можно сказать, что в ориентированном графе потомством вершины х, обозначен­ным как Р(х), называется множество всех вершин, в которые ведут пути из х.

Тогда если существует некоторая вершина 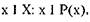то в графе G имеется

цикл.

Первая теорема; цикл в графе повторно используемых ресурсов является необхо­димым условием тупика.

Для доказательства этой теоремы (которое мы опустим¹) можно воспользоваться следующим свойством ориентированных графов: если ориентированный граф не содержит цикла, то существует линейное упорядочение вершин такое, что если существует путь от вершины i к вершине], то i появляется перед j в этом упорядо­чении.

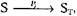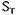Вторая теорема: если S не является состоянием тупика и где есть

состояние тупика, в том и только в том случае, когда операция процесса 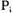есть запрос и 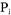находится в тупике в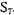

Это следует понимать таким образом, что тупик может быть вызван только при запросе, который не удовлетворен немедленно. Учитывая эту теорему, можно сде­лать вывод, что проверка на тупиковое состояние может быть выполнена более эффективно, если она проводится непрерывно, то есть по мере развития процес­сов. Тогда надо применять редукцию графа только после запроса от некоторого

' При желании его можно найти в [54].

272_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

процесса 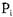и на любой стадии необходимо сначала попытаться сократить граф с помощью процесса 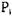. Если процесс 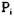смог провести сокращение графа, то ника­кие дальнейшие сокращения не являются необходимыми.

Ограничения, накладываемые на распределители, на число ресурсов, запрошен­ных одновременно, и на количество единиц ресурсов, приводят к более простым условиям для тупика.

Пучок, или узел, в ориентированном графе G = <Х, Е> — это подмножество вер­шин Z I X, таких что 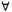х I Z, Р(х) = Z, то есть потомством каждой вершины из Z является само множество Z. Каждая вершина в узле достижима из каждой другой вершины этого узла, и узел есть максимальное подмножество с этим свойством. Поясним сказанное рис. 8.10.

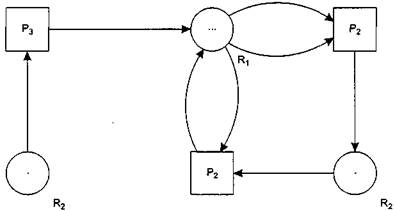
Рис. 8.10. Пример узла в модели Холта

Следует заметить, что наличие цикла — это необходимое, но не достаточное условие для узла. Так, на рис. 8.11 изображены два подграфа. Подграф а пред­ставляет собой пучок (узел), тогда как подграф б представляет собой цикл, но узлом не является. В узел должны входить дуги, но они не должны из него вы­ходить.

Если состояние системы таково, что удовлетворены все запросы, которые мо­гут быть удовлетворены, то существует простое достаточное условие существо­вания тупика. Эта ситуация возникает, если распределители ресурсов не от­кладывают запросы, которые могут быть удовлетворены, а выполняют их по возможности немедленно (большинство распределителей следуют именно этой дисциплине).

Состояние называется фиксированным, если каждый процесс, выдавший запрос, заблокирован.

Третья теорема: если состояние системы фиксированное (все процессы, имею­щие запросы, удовлетворены), то наличие узла в соответствующем графе повтор­но используемых ресурсов является достаточным условием тупика.

Методы борьбы с тупиками___________________________________________ 273

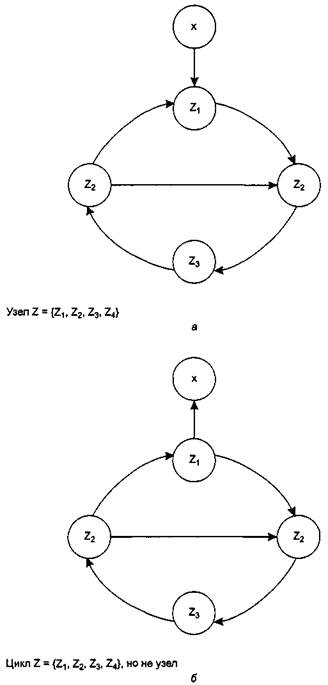
Рис. 8.11. Узел и цикл в ориентированном графе

274_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

Для доказательства предположим, что граф содержит узел Z. Тогда все процессы в этом узле должны быть заблокированы только по ресурсам, принадлежащим Z, так как никакие ребра не могут выходить из Z по определению. Аналогично, по той же самой причине все распределенные ресурсы узла Z принадлежат процессам из Z. Наконец, все процессы в Z должны быть заблокированы согласно условию фикси­рованности и определению узла. Следовательно, все процессы в узле Z должны быть в тупике.

Допустим, что каждый ресурс имеет единичную емкость (по одной единице ресур­са), то есть 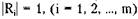. При этом ограничении наличие цикла также становится достаточным условием тупика.

Четвертая теорема: граф повторно используемых ресурсов с единичной емкос­тью указывает на состояние тупика тогда и только тогда, когда он содержит цикл. Необходимость цикла доказывает первая теорема. Для доказательства достаточ­ности допустим, что граф содержит цикл, и рассмотрим только лишь процессы и ресурсы, принадлежащие циклу. Так как каждая вершина-процесс должна иметь входящее и исходящее ребра, она должна выдать запрос на некоторый ресурс, при­надлежащий циклу, и должна удерживать некоторый ресурс, принадлежащий тому же циклу. Аналогично, каждый ресурс единичной емкости в цикле должен быть захвачен некоторым процессом. Следовательно, каждый процесс в цикле блоки­руется на ресурсе, который может быть освобожден только некоторым процессом из этого цикла; поэтому процессы в цикле находятся в тупике.

Чтобы обнаружить тупик в случае ресурса единичной емкости, мы должны просто проверить граф повторно используемых ресурсов на наличие циклов.

Алгоритм обнаружения тупика по наличию замкнутой цепочки запросов

Итак, распознавание тупика может быть основано на анализе модели распределе­ния ресурсов. Один из алгоритмов, основанный на методе обнаружения замкну­той цепи запросов, был разработан сотрудниками фирмы IBM и применялся в од­ной из ОС этой компании. Он использует информацию о состоянии системы, содержащуюся в двух таблицах: таблице текущего распределения (назначения) ресурсов RATBL и таблице заблокированных процессов PWTBL (для каждого вида ресурса может быть свой список заблокированных процессов). При каждом за­просе на получение или освобождение ресурсов содержимое этих таблиц модифи­цируется, а запрос анализируется в соответствии со следующим алгоритмом [22].

1. Начало алгоритма. Приходит запрос от процесса с номером J на занятый ресурс
с номером I.

2. Поместить номер ресурса I в таблицу PWTBL в строке с номером процесса J.

3. Использовать I в качестве смещения в таблице RATBL, чтобы найти номер про­
цесса К, который владеет ресурсом.

4. Использовать К в качестве смещения в таблице PWTBL.

5. Проверить, ждет ли процесс с номером К освобождения какого-либо ресурса с
номером Г. Если нет, то перейти к шагу 6, в противном случае — к шагу 7.

Методы борьбы с тупиками____________________________________________ 275

6. Перевести процесс с номером J в состояние ожидания и выйти из алгоритма.

7. Использовать Г в качестве смещения в таблице RATBL, чтобы найти номер К'
блокирующего его процесса.

8. Проверить, что К' = J. Если нет, перейти к шагу 9, в противном случае — к ша-
гуП.

9. Проверить, вся ли таблица PWTBL просмотрена. Если да, то перейти к шагу
6, в противном случае — к шагу 10.

10. Присвоить К := К' и перейти к шагу 4.

11. Сделать вывод о наличии тупика с последующим восстановлением.

12. Конец алгоритма.

Для иллюстрации описанного алгоритма распознавания тупика рассмотрим сле­дующую последовательность событий.

1. Процесс Р1 занимает ресурс R1.

2. Процесс Р2 занимает ресурс R3.

3. Процесс РЗ занимает ресурс R2.

4. Процесс Р2 занимает ресурс R4.

5. Процесс Р1 занимает ресурс R5.

В результате таблица распределения ресурсов (RATBL) принимает такой вид, как показано в табл. 8.3.

Таблица 8.3.Таблица распределения ресурсов

Ресурсы Процессы

_ _

R2 РЗ

R3 Р2

R4 Р2

R5_____________ Р1________________________________________________________________

6. Пусть процесс Р1 пытается занять ресурс R3, поэтому в соответствии с описан­
ным алгоритмом J = 1,1 = 3, К = 2. Процесс К не ждет никакого ресурса, поэто­
му процесс Р1 блокируется по ресурсу R3.

7. Далее, пусть процесс Р2 пытается запять ресурс R2: J = 3,1 = 2, К = 3. Процесс
с номером К=3 не ждет никакого ресурса, поэтому процесс Р2 блокируется по
ресурсу R2.

8. И наконец, пусть процесс РЗ пытается обратиться к ресурсу R5: J = 3, I = 5,
К = 1, Г = 3, К¹ = 2, К¹ <> J, поэтому берем К = 2, I = 2, К' = 3.

В этом случае К' = J, то есть тупик определен. Таблица заблокированных процес­сов (PWTBL) теперь будет выглядеть так, как показано в табл. 8.4. Равенство J = К' означает, что существует замкнутая цепь взаимоисключающих и ожидающих процессов, то есть выполняются все четыре условия существования тупика.

276_______________________ Глава 8. Проблема тупиков и методы борьбы с ними

Таблица 8.4.Таблица заблокированных ресурсов

Процесс Ресурс

__ _

Р2 R2

РЗ_____________ R5_______________________________________________________________

Для описанного нами примера можно построить модель Холта, как показано на рис. 8.12. Здесь пронумерованы дуги запросов, которые процессы последователь­но генерировали в соответствии с нашим примером. Из рисунка сразу видно, что в результате такой последовательности запросов образовалась замкнутая цепоч­ка: (8, 5, 6, 2, 7, 3), что и говорит о существовании тупика.

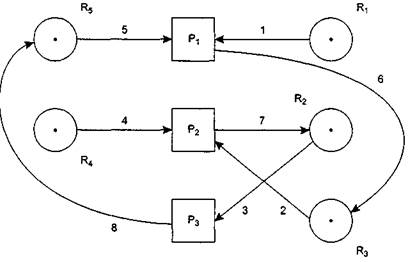
Рис. 8.12. Граф распределения ресурсов

Распознавание тупика требует дальнейшего восстановления вычислений.

Восстановление можно интерпретировать как запрет постоянного пребывания в опасном состоянии. Существуют следующие методы восстановления:

- принудительный перезапуск системы, характеризующийся потерей информа­
ции обо всех процессах, существовавших до перезапуска;

- принудительное завершение процессов, находящихся в тупике;

- принудительное последовательное завершение процессов, находящихся в ту­пике, с последующим вызовом алгоритма распознавания после каждого завер­шения до исчезновения тупика;

- перезапуск процессов, находящихся в тупике, с некоторой контрольной точки, то есть из состояния, предшествовавшего запросу на ресурс;

- перераспределение ресурсов с последующим последовательным перезапуском
процессов, находящихся в тупике.

Контрольные вопросы и задачи_________________________________________ 277

Основные издержки восстановления составляют потери времени на повторные вычисления, которые могут оказаться весьма существенными. К сожалению, в ряде случаев восстановление может стать невозможным, например исходные данные, поступившие с каких-либо датчиков, могут измениться, тогда предыдущие значе­ния будут безвозвратно потеряны.

Контрольные вопросы и задачи

1. Что такое тупиковое состояние? Приведите несколько примеров возникнове­
ния тупиковой ситуации.

2. Что является причиной возникновения тупиков на ресурсах типа SR? Пере­
числите условия, при которых возникает тупик.

3. Приведите пример графа повторно используемых ресурсов. Что позволяет сде­
лать эта модель Холта?

4. Приведите пример теоретико-множественного описания сети Петри.

5. Что такое маркировка сети Петри? Что представляет собой пространство воз­
можных состояний сети Петри?

6. Приведите пример графического представления сети Петри.

7. Что следует предпринять для реализации стратегии предотвращения тупико­
вых ситуаций? Какие реальные проблемы при этом возникают?

8. Что представляет собой «обход тупика»? Приведите алгоритм банкира Дейк-
стры. Почему на практике невозможно воспользоваться алгоритмом банкира
для борьбы с тупиковыми ситуациями?

9. Что такое «опасное состояние»? Приведите пример опасного состояния на мо­
дели состояний системы.

10. Опишите метод обнаружения тупика посредством редукции графа повторно
используемых ресурсов.

11. Опишите алгоритм обнаружения тупика по наличию замкнутой цепочки за­
просов.

Глава 9. Архитектура операционных систем

Как комплекс системных управляющих и обрабатывающих программ (см. главу 1), операционная система представляет собой очень сложный конгломерат взаимо­связанных программных модулей и структур данных, которые должны обеспечи­вать надежное и эффективное выполнение вычислений. Большинство потенци­альных возможностей операционной системы, ее технические и потребительские параметры — все это во многом определяется архитектурой системы — ее структу­рой и основными принципами построения.

В г лаве 1 мы упомянули несколько наиболее распространенных классификаций. Очевидно, что системы, ориентированные на диалог, должны иметь иные страте­гию обслуживания и дисциплину диспетчеризации, чем системы пакетной обра­ботки. Диалоговое взаимодействие предполагает реализацию развитой интерфей­сной подсистемы, обеспечивающей взаимодействие пользователя с компьютером. Это отличие сказывается и на особенностях построения систем. Очевидно, что для диалоговых операционных систем необходимо предусмотреть множество механиз­мов, которые позволят пользователям эффективно управлять своими вычислени­ями.

Аналогично, и системы, реализующие мультизадачный режим работы, отличают­ся по своему строению от однозадачных систем. Если система допускает работу нескольких пользователей, то желательно иметь достаточно развитую подсистему информационной безопасности. А это, в свою очередь, налагает определенные тре­бования и на идеологию построения операционной системы, и на выбор конкрет­ных механизмов, помогающих реализовать защиту информационных ресурсов и ввести ограничения на доступ к другим видам ресурсов. Поскольку операционные системы помимо функций организации вычислений и организации интерфейса пользователя предоставляют интерфейсы для взаимодействия программ с опера­ционной системой, мы в этой главе рассмотрим и интерфейсы прикладного про­граммирования.

Основные принципы построения операционных систем_______________________ 279