Распределение вероятности ожидаемых доходов по двум инвестиционным проектам

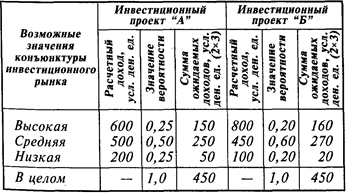
Более наглядное представление об уровне риска дают результаты расчета среднеквадратического (стан­дартного) отклонения, представленные в табл. 3.3.

Таблица 3.3.

Расчет среднеквадратического (стандартного) отклонения по двум инвестиционным проектам

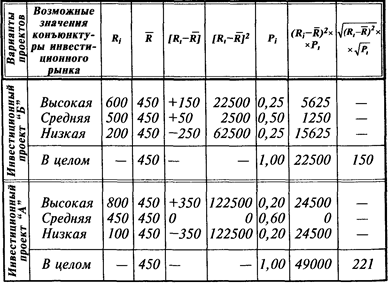
Результаты расчета показывают, что средне-квадратическое (стандартное) отклонение по ин­вестиционному проекту "А " составляет 150, в то время как по инвестиционному проекту "Б" — 221, что свидетельствует о большем уровне его риска.

Рассчитанные показатели среднеквадратиче­ского (стандартного) отклонения по рассматривае­мым инвестиционным проектам могут быть интер­претированы графически (рис. 3.11.)

Из графика видно, что распределение вероят­ностей проектов "А " и "Б " имеют одинаковую вели­чину расчетного дохода, однако в проекте "А " кри­вая уже, что свидетельствует о меньшей колебле­мости вариантов расчетного дохода относительно средней его величины R, а следовательно и о меньшем уровне риска этого проекта.

Вероятность

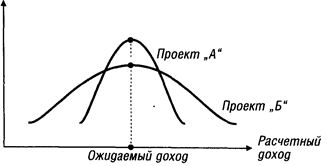
Рисунок 3.11. Распределение вероятности ожидаемого (расчетного) дохода по двум инвести­ционным проектам.

г) Коэффициент вариации. Он позволяет определить Уровень риска, если показатели среднего ожидаемого дохода от осуществления финансовых операций разли­чаются между собой. Расчет коэффициента вариации осуществляется по следующей формуле:

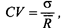
где CV— коэффициент вариации;

σ—среднеквадратическое (стандартное) отклонение;

R—среднее ожидаемое значение дохода по рас­сматриваемой финансовой операции.

Пример: Необходимо рассчитать коэффициент вариации по трем инвестиционным проектам при раз­личных значениях среднеквадратического (стандарт­ного) отклонения и среднего ожидаемого значения дохода по ним. Исходные данные и результаты рас­чета приведены в табл 3 4

Таблица 3 4.

Расчет коэффициента вариации по трем инвестиционным проектам

Результаты расчета показывают, что наимень­шее значение коэффициента вариации — по проекту "А", а наибольшее — по проекту "В" Таким обра­зом, хотя ожидаемый доход по проекту "В" на 33% выше, чем по проекту "А" ((600 – 450) / 450 х 100) , уровень риска по нему, определяемый коэффициентом вариации, выше на 61% )(0,53 – 0,33) / 0,33 х 100)

Следовательно, при сравнении уровней рисков по отдельным инвестиционным проектам предпоч­тение при прочих равных условиях следует отдавать тому из них, по которому значение коэффициентов вариации самое низкое (что свидетельствует о наи­лучшем соотношении доходности и риска).

д) Бета-коэффициент (или бета) Он позволяет оце­нить индивидуальный или портфельный систематичес­кий финансовый риск по отношению к уровню риска финансового рынка в целом. Этот показатель использу­ется обычно для оценки рисков инвестирования в от­дельные ценные бумаги. Расчет этого показателя осу­ществляется по формуле:

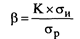
где β—бета-коэффициент;

К — степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;

σ_и — среднеквадратическое (стандартное) отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);

σ_р — среднеквадратическое (стандартное) отклонение доходности по фондовому рынку в целом.

Уровень финансового риска отдельных ценных бу­маг определяется на основе следующих значений бета-коэффициентов:

Β = 1— средний уровень,

β > 1 — высокий уровень,

β < 1 — низкий уровень.

2 Экспертные методы оценки уровня финансового риска применяются в том случае, если на предприятии отсутствуют необходимые информативные данные для осуществления расчетов экономико-статистическими методами. Эти методы базируются на опросе квалифици­рованных специалистов (страховых, финансовых, инвести­ционных менеджеров соответствующих специализиро­ванных организаций) с последующей математической обработкой результатов этого опроса.

В целях получения более развернутой характеристи­ки уровня риска по рассматриваемой операции опрос следует ориентировать на отдельные виды финансовых рисков, идентифицированные по данной операции (про­центный, валютный, инвестиционный и т.п.).

В процессе экспертной оценки каждому эксперту предлагается оценить уровень возможного риска, осно­вываясь на определенной балльной шкале, например

— риск отсутствует: 0 баллов;

— риск незначительный: 10 баллов;

— риск ниже среднего уровня: 30 баллов;

— риск среднего уровня: 50 баллов;

— риск выше среднего уровня: 70 баллов;

— риск высокий: 90 баллов;

— риск очень высокий: 100 баллов.

3 Аналоговые методы оценки уровня финансового риска позволяют определить уровень рисков по отдельным наиболее массовым финансовым операциям предприя­тия. При этом для сравнения может быть использован как собственный, так и внешний опыт осуществления таких финансовых операций

II Методический инструментарий формирования не­обходимого уровня доходности финансовых операций с учетом фактора риска позволяет обеспечить четкую ко­личественную пропорциональность этих двух показате­лей в процессе управления финансовой деятельностью предприятия

1. При определении необходимого уровня премии за риск используется следующая формула

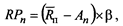
где RPn— уровень премии за риск по конкретному финансовому (фондовому) инструменту,

Rп — средняя норма доходности на финансовом

рынке,

Аn — безрисковая норма доходности на финансо­вом рынке,

β — бета-коэффициент, характеризующий уровень систематического риска по конкретному фи­нансовому (фондовому) инструменту

Пример: Необходимо рассчитать уровень пре­мии за риск по трем видам акции Исходные данные и результаты расчета приведены в табл 3.5

Таблица 3 5