Механизмы послойного роста

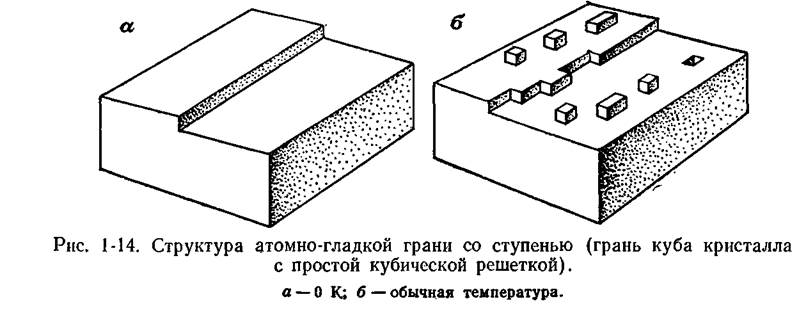
У частицы, адсорбированной на атомно-гладкой поверхности, число ближайших соседей (и соответственно глубина потенциаль­ных ям) гораздо меньше, чем в случае адсорбции на шероховатой поверхности. Прочного закрепления не происходит, и частицы легко десорбируются. Поэтому на идеальных сингулярных поверхностях нет мест присоединения. Пусть теперь на сингулярной грани имеется ступень, аналогичная ступеням вицинальных по­верхностей (§ 1.1). Расчеты показывают [Бартон В. и др., 1959], что при обычных температурах, задолго до точки плавления, торцы ступеней размыты тепловым движением частиц — шероховаты (рис. 1-14), т. е. вдоль ступеней существуют цепочки глубоких потенциальных ям.

Частица, попавшая в излом на ступени, имея большое число уже закрепленных соседей, прочно присоединяется к кристаллу. Поскольку торец ступени шероховат, т. е. изломов много, присо­единение может происходить практически в любом месте ступени, и ступень продвигается по нормальному механизму. Дойдя до ребра, эта ступень исчезает. Таким образом, при проходе ступени от одного края грани до другого грань продвинется на расстояние, равное высоте ступени. Такой способ роста за счет распространения слоев называется послойным (слоистым, тангенциальным) ростом.

Сами по себе за счет тепловых флуктуации ступени на гладких гранях возникать практически не могут.

Однако гладкие грани растут и, как показывают многочисленные наблюдения, растут именно послойно. Существует два механизма образования ступеней на гладких гранях: дислокационный и механизм двумерного зарождения; они подробно обсуждаются в книге Р. Ф. Стрикленд-Констэбл [1971].

Дислокационный механизм роста

Если на грань кристалла выходит винтовая дислокация, на этой грани имеется ступень высотой, равной вектору Бюргерса дислокации (рис. 1-1). При росте кристалла торец этой ступени будет служить местом присоединения частиц.

Если за начальную принять прямолинейную форму ступени, то при постоянстве скорости присоединения частиц к любой точке ступени (постоянстве линейной скорости роста ступени) ступень закручивается в спираль (рис. 1-15). При этом над местом выхода дислокации возникает конусообразное возвышение — конус или холмик роста. Холмик роста, ограненный плоскими (вицинальными) гранями, называется вицинальной пирамидой (вициналью).

В случае медленного растворения наблюдается обратное движе­ние ступени с образованием ямки травления на месте выхода дис­локации.

На сингулярных поверхностях, как правило, присутствуют хол­мики роста самых разных размеров, вплоть до различимых нево­оруженным глазом. Нередко удается наблюдать их спиральный характер (рис. 1-16). Заметим, что особенности роста на дислокациях таковы, что описываемый холмик может иметь спиральный характер только вблизи своего центра.

Спирали могут быть одно- и многозаходные, контуры спираль­ных ступеней могут быть округлыми (гладкими) и многоугольными (полигональными). При малых пересыщениях симметрия полигональных контуров ступеней подчиняется симметрии граней, высота ступеней невелика и конус, имея при вершине угол, близкий к 180°, почти не виден. При этом боковые поверхности конусов роста иногда образуют макроскопически гладкие вицинальные грани, дающие в отраженном свете отдельные отблески. При увеличении пересыщения расстояние между ступенями уменьшается, соответственно увеличивается крутизна конусов; рельеф поверхности становится резким, контрастным. Одновременно контуры ступеней обычно становятся округлыми.

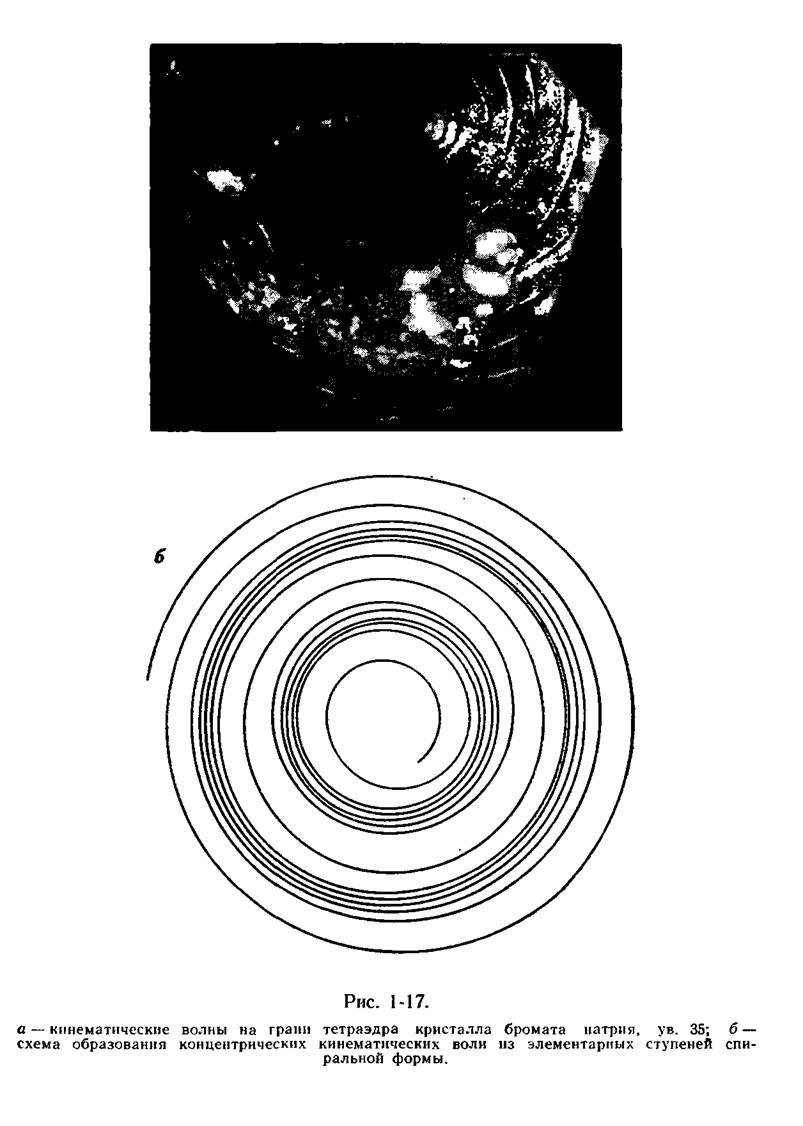
Контрастность рельефа при неизменной высоте элементарных ступеней может увеличиваться за счет появления на грани так на­зываемых кинематических волн плотности ступеней.

Появление таких волн, представляющих собой сгущения элементарных ступеней (рис. 1-17), обусловлено особенностями диффузионного поля вблизи центров роста. На рис. 1-17, а не видны элементарные ступени (высотой, равной вектору Бюргерса), образовавшие кольцеобразные кинематические волны, но сами волны видны прекрасно и дают возможность легко найти центр роста (вершину конуса). Кинематические волны в ряде случаев видны даже невооруженным глазом. Элементарные ступени требуют для своего обнаружения специальных тонких методик исследования поверхности: элек­тронной микроскопии, многолучевой интерферометрии [ФЭС, 1962—1966 гг.].

Еще раз подчеркнем, что холмики роста наблюдаются практически на всех кристаллах, выращиваемых из низкотемпературных растворов. Образование этих форм рельефа граней на выходах винтовых дислокаций подтверждается, в частности, путем травления граней октаэдра кристаллов А1 — К-квасцов и тетраэдра бромата натрия.

Конусы роста образуются, как правило, не на одиночных дислокациях, а на скоплениях дислокаций. Показано [Бартон В. и др., 1959], что чем больше дислокаций одного знака входит в группу, тем она активнее (т. е. тем больше она генерирует слоев в единицу времени). Если на грани работает одновременно несколько групп дислокаций, то слои, испускаемые наиболее активной группой, могут подавлять работу остальных групп и одиночных дислокаций. Поэтому, хотя плотность дислокаций, как уже указывалось, высока, в стабильных условиях на поверхности грани обычно действует всего несколько центров роста, а иногда и один. Если же изменить пересыщение, то поверхность покрывается множеством мелких конусов роста. В течение какого-то времени идет отбор, кончающийся тем, что на грани опять остается несколько наиболее активных центров роста, причем это могут быть и новые, но ранее не активные.

При возвращении к прежнему пересыщению после периода множественного проявления центров восстанавливается деятельность старых центров роста.

Иногда, особенно в присутствии примесей, тормозящих распространение слоев (§ 1.7), возникновение множества конусов роста на грани наблюдается и в стабильных условиях роста. При этом, если холмы роста относительно изометричны (т. е. скорость движения слоев от центра в разных направлениях примерно одинакова), возникает поверхность типа «булыжной мостовой» [грань (111) кристаллов пентаэритрита], как и при уже упоминавшемся нормальном росте пинакоида кварца. Если же холмы роста сильно вытянуты, на грани образуется «вицинальная штриховка» (медный купорос, эпсомит и т. д.) *.

Основной источник дислокации в кристалле — это либо напряжения, вызванные неравномерным вхождением примесей в решетку (§ 1.8), либо термические напряжения. Установлены также некоторые частные способы образования дислокаций при росте. Так, Г. Г. Леммлейн и Е. Д. Дукова наблюдали возникновение дислокаций при срастании ветвей скелетного кристалла (о скелетах см. в § 1.6). М. И. Козловский [1958] описал возникновение дислокаций при слоистом обрастании кристаллом твердых частиц, осевших на его поверхность. Аналогично возникает большое число дислокаций при смыкании слоев над жидкостными включениями [Хаджи В. Е., 1966], в частности при обычном захвате включений при регенерации. Не случайно поэтому наблюдается преимущественное расположение ямок травления на гранях над затравками. Подробно возникновение дислокаций в кристаллах при росте рассмотрено Е. П. Костюковой и др. [1977].

Группы дислокаций, возникших при захвате включений при регенерации, сплошь и рядом оказываются весьма активными, а потому конусы роста обычно располагаются над затравкой, в средних частях граней. Вообще, чем больше дислокаций в кристалле, тем, естественно, больше вероятность наличия среди них более мощных активных группировок. Поэтому скорость роста кристалла, как правило, тем больше, чем более дефектен кристалл. Этот давно известный факт получил объяснение лишь на основе дислокационных представлений о росте.

Дислокации, как уже говорилось, не могут обрываться внутри однородного кристалла. Однако они могут перекрываться включением. При этом часть дислокаций противоположного знака будет исчезать, замыкаясь друг на друга в объеме включения. Другая часть может менять ориентацию, переходя, в частности, в краевые дислокации.

От вицинальной штриховки следует отличать «комбинационную штриховку», обусловленную комбинацией граней разных простых форм или одной формы (ис-штрихованные грани пентагондодекаэдра на кубообразных кристаллах пирита). Появление такой штриховки — способ замещения старой формы кристалла на новую при смене внешних условий.

Таким образом, число дислокаций, возникающих за счет неточного смыкания слоев над включением, может оказаться меньше, чем число дислокаций, перекрытых включением, так что υ ~ (∆m/m_o)ⁿ, а показатель степени п обычно заключен в интервале от 1 до 2. Типичная кривая скорости дислокационного роста показана на рис. 1-13.

Если зависимость скорости роста от пересыщения слабо нелинейна, ее трудно отличить от прямолинейной зависимости характерной для нормального роста, особенно при изучении этой зависимости на небольшом отрезке пересыщений. Поэтому измерение скоростей следует сопровождать изучением скульптуры граней, установлением атомарного типа грани и ее дефектности. Наличие различимых в оптический микроскоп отдельных центров роста, по-видимому, достаточное свидетельство дислокационного механизма.

Рост двумерными зародышами

Если несколько частиц адсорбируется в соседних позициях, то образованный ими островок может оказаться стабильным и дать начало новому слою. Эти островки называются двумерными зародышами. Закономерности образования двумерных и трехмерных зародышей в объеме раствора (§ 1.4) аналогичны.

Преобладание дислокационного роста во множестве изученных случаев является свидетельством малой вероятности образования устойчивых двумерных зародышей в сравнительно широком интервале пересыщений.

С ростом пересыщения размер критического двумерного зародыша уменьшается, и при достижении относительного пересыщения, равного по теории нескольким десяткам процентов, существование жизнеспособных двумерных зародышей на грани становится достаточно вероятным. По достижении этого пересыщения грань начинает быстро расти. Зависимость скорости роста от пересыщения при этом механизме, как и скорость образования трехмерных зародышей, носит экспоненциальный характер (рис. 1-13).

Такая зависимость скорости роста от пересыщения подтверждена экспериментально на примере роста кристалла из пара. Что касается роста из раствора, то, хотя подобные зависимости и встречаются, по ним обычно нельзя однозначно сказать, что рост происходил двумерными зародышами. Дело в том, что в присутствии некоторых примесей и при дислокационном механизме роста получаются сходные зависимости (§ 1.7). По наблюдению за поверхностью грани, ее морфологией также трудно установить, имеется ли рост двумерными зародышами, поскольку толщина их равна периоду повторяемости в данной решетке. В. Косселем и И. Странским было показано, что для ионных кристаллов наиболее энергетически выгодно образование двумерных зародышей у ребер гладкой грани. Атомарные слои, образовавшиеся за счет этих зародышей, могут сливаться в макроскопические слои благодаря особенностям диффузионного поля около кристалла (§ 1.6). Поэтому наблюдающееся образование слоев у вершин и ребер обычно считается признаком роста по механизму двумерного зародышеобразования.

Однако образование видимых слоев у ребер и вершин кристалла может происходить и при дислокационном механизме, также благодаря особенностям диффузионного поля, и, таким образом, оно не является однозначным признаком двумер­ного зародышеобразования. Если внешне грань гладкая, то вопрос о механизме роста остается открытым, так как центры роста вблизи ребер могут быть просто неразличимы.

Наиболее изящно было показано существование двумерного зарождения при электрокристаллизации серебра [Будевский Е. и др., 1974]. Кристаллы росли в капиллярах, где сравнительно легко получить бездислокационную грань благодаря выходу дислокаций на боковую поверхность кристалла. При отсутствии выходов дислокаций на торце кристалла и подаче соответствующего напряжения на систему кристалл — раствор ток проходил отдельными импульсами. Так как ток проходит только в момент кристаллизации, то он при дислокационном росте должен быть непрерывным. Установлено, что количество электричества, протекающего за один импульс, соответствует числу электронов, необходимому для восстановления того количества серебра, которое перекрывает пло­щадь капилляра моноатомным слоем.

Иногда кристаллы КС1, КВг, которые обычно изометричны, образуются в виде тонких кристаллических волокон — усов (подробнее об усах см. в книгах Г. В. Бережковой [1969], Е. И. Гиваргизова [1977 г.]). Боковые грани усов не имеют выходов винтовых дислокаций, поэтому утолщение усов может происходить только путем двумерного зародышеобразования. Для кристаллов нор­мального габитуса при обычном росте из растворов достоверных примеров их образования по механизму двумерного зарождения почти нет. Рост грани дипирамиды (101) кристаллов КН₂Р0₄ при переохлаждениях свыше 14° С (относительное пересыщение 29%) идет, видимо, по рассматриваемому механизму [Белюстин А. В., Степанова Н. С, 1980]. Эта грань в процессе роста освобождается от дефектов (рис. 1-18) и не растет при переохлаждениях ниже 14° С. Мы практически всегда наблюдали работу дислокационных центров роста вплоть до пересыщений, когда в объеме раствора начинается трехмерное зарождение.

Замещение быстрорастущих шероховатых граней медленнорас­тущими сингулярными определяет обычную плоскогранную форму кристаллов. Сингулярные грани с разной плотностью ступеней различаются скоростями роста, соотношение которых определяет облик (огранку и габитус)* кристалла. Быстро растущие грани, как правило, уменьшаются в размерах, и огранка определяется наиболее медленно растущими сингулярными гранями. Обычно кристалл огранен небольшим числом кристаллических форм, кото­рым отвечают малые значения рациональных символов.

Скорости роста кристалла в кристаллографически разных направлениях различны, но при заданных условиях относительно постоянны во времени.

* Под огранкой понимается совокупность кристаллографических форм (граней), под габитусом — общая форма кристалла (изометрическая или анизометрическая: игольчатая, призматическая, пластинчатая и т. п.).

Можно построить полярную диаграмму скоростей, по виду аналогичную полярной диаграмме поверхностной энергии (рис. 1-5).

Закономерности в скоростях роста кристаллов рассматриваются в разделе кристаллогенезиса, называемом кинетикой.