Операции с классами

При помощи логических операций из двух или нескольких клас­сов могут быть образованы новые классы. К этим операциям отно­сятся: объединение классов, вычитание классов, пересечение классов и образование дополнения к классу.

Операция объединения классов (сложение)состоит в объедине­нии двух или нескольких классов в один класс, состоящий из всех элементов, входящих в слагаемые классы.

Операция объединения классов записывается с помощью знака сложения А È не-А. Множество, полученное в результате сложения, называется суммой (на схеме полученное множество заштриховано).

Складывать можно множества, находящиеся в любых отношени­ях, например множества, входящие в понятия, находящиеся в отно­шении подчинения: «юрист» (В) и «следователь» (А). Множество, полученное в результате сложения, включает юристов-следователей и юристов-неследователей (рис. 14). Объединяя классы, находящие­ся в отношении частичного совпадения: «юрист» (А) и «депутат Государственной Думы» (В), — получим множество, объединяющее юристов-недепутатов (1), юристов-депутатов (2) и депутатов-не­юристов (3) — рис. 15.

Операция вычитания классов дает класс, состоящий из элемен-тов, исключающих элементы вычитаемых классов. Вычитая, напри­мер, элементы класса «следователь» (А) из класса «юрист» (В), полу­чаем класс юристов не-следователей (рис. 16). Вычитая элементы класса «юрист» (А) из класса «депутат Государственной Думы» (В), получаем класс депутатов Государственной Думы, не являющихся юристами. Множество, полученное в результате вычитания классов, заштриховывается (рис. 17).

Операция пересечения классов (умножение) состоит в отыскании элементов, общих для двух или нескольких классов (множеств). Так, в результате умножения множеств, мыслящихся в понятиях «юрист» (А) и «депутат» (В), получаем новое множество: юристов-депутатов (рис. 18).

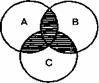
Операция пересечения классов записывается с помощью знака умножения: А Ç В. Множество, полученное в результате умноже­ния, называется произведением (заштрихованная часть схемы). Ум­ножать можно три и больше множеств. Так, умножая множества, входящие в понятия «юрист» (А), «депутат» (В) и «москвич» (С), получаем множество юристов, являющихся депутатами и москвича­ми (рис. 19).

При умножении множеств, входящих в несовместимые понятия, например «следователь» и «адвокат», получаем нулевой (пустой) класс, так как элементов, входящих одновременно в оба понятия, не существует.

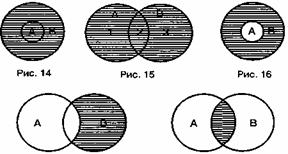
Образование дополнения (отрицание).Дополнением к классу Аназывается класс не-А (А'), который при сложении с А образует универсальную область. Эта область представляет собой универ­сальный класс и обозначается знаком 1. Чтобы образовать дополне­ние, нужно класс А исключить из универсального класса: 1 - А = А'. Образование дополнения состоит, таким образом, в образовании

нового множества путем исключения данного множества из универ­сального класса, в который оно входит. Так, исключая множество адвокатов из универсального класса юристов, образуем дополнение: множество юристов-неадвокатов. В своей сумме оба понятия обра­зуют весь универсальный класс, соответствующий понятию «юрист» (рис. 20).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем сущность и практическое значение логических операций обобщения и ограничения понятий?

2. Что такое определение понятия (дефиниция)? Укажите виды определения.

3. Как строится определение через род и видовое отличие? Каковы его правила и ошибки, связанные с их нарушением?

4. Охарактеризуйте приемы, сходные с определением.

5. Что такое деление понятия? Укажите виды деления.

6. Каким правилам подчиняется операция деления, какие логические ошибки возникают при их нарушении?

7. Что такое классификация?

8. В чем состоит значение определения и деления понятий в научной и практичес­кой деятельности?

9. Что представляют собой логические операции с классами?

Глава IV СУЖДЕНИЕ